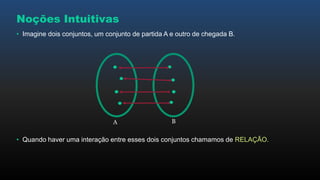
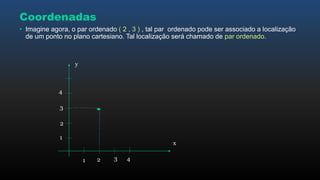
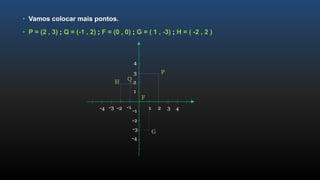
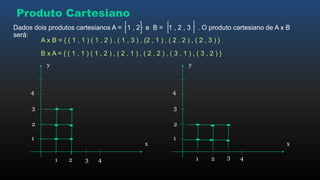
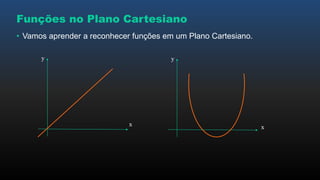
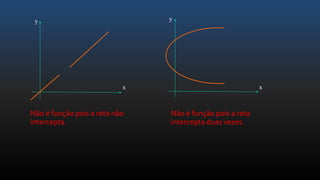
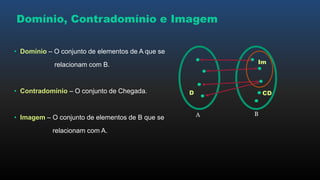
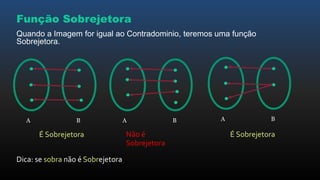
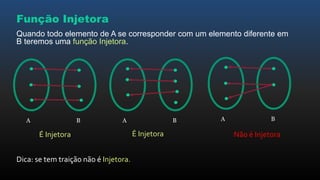
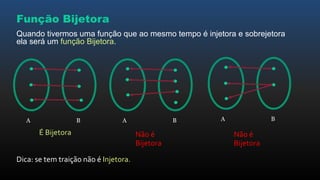
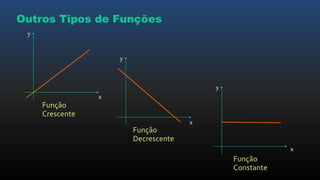
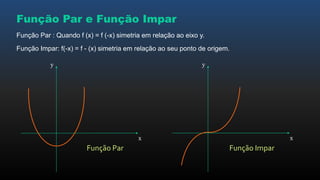
O documento apresenta os conceitos básicos de funções, incluindo noções intuitivas de conjuntos de partida e chegada e relações, funções no plano cartesiano, domínio, contradomínio e imagem, tipos de funções como injetora, sobrejetora e bijetora, e leis de formação de funções.

1. Conceito Básico de
Funções
ÁLGEBRA I

2. Noções Intuitivas
• Imagine dois conjuntos, um conjunto de partida A e outro de chegada B.
• Quando haver uma interação entre esses dois conjuntos chamamos de RELAÇÃO.
A B

3. • Agora imagine um caso especial de relação.
• Todo elemento do conjunto de partida se corresponde com apenas um elemento do
conjunto de chegada.
• Quando isso acontece chamamos isso de FUNÇÃO.
A B A B A B
A B A B
É Função É Função É Função
Não é Função Não é Função

4. Plano Cartesiano
• Formado por duas retas x e y ortogonais com um ângulo de 90° a reta x horizontal recebe
o nome de abcissa e a reta y na vertical que recebe o nome de ordenada.
x
y

5. Par Ordenado
• Imagine dois conjuntos x e y, imagine que a é um elemento de x e que b seja um elemento
de y. Se esses dois elementos estiverem em correspondência o par ordenado (a , b) ira
representar (nessa ordem) um elemento de x seguido do elemento de y.
• Ar ordenado depende de ordem, ou seja (a , b) = (b , a)
x y
a
b ( a , b )

6. • Imagine agora, o par ordenado ( 2 , 3 ) , tal par ordenado pode ser associado a localização
de um ponto no plano cartesiano. Tal localização será chamado de par ordenado.
x
y
Coordenadas
1
21 3 4
2
3
4

7. • Vamos colocar mais pontos.
• P = (2 , 3) ; Q = (-1 , 2) ; F = (0 , 0) ; G = ( 1 , -3) ; H = ( -2 , 2 )
1
2
3
4
-1
-2
-3
-4
1 2 3 4-1-2-3-4
P
Q
F
G
H

8. Produto Cartesiano
Dados dois produtos cartesianos A = 1 , 2 e B = 1 , 2 , 3 . O produto cartesiano de A x B
será:
A x B = { ( 1 , 1 ) ( 1 , 2 ) , ( 1 , 3 ) , (2 , 1 ) , ( 2 , 2 ) , ( 2 , 3 ) }
B x A = { ( 1 , 1 ) ( 1 , 2 ) , ( 2 , 1 ) , ( 2 , 2 ) , ( 3 , 1 ) , ( 3 , 2 ) }
x
y
1
21 3 4
2
3
4
x
y
1
21 3 4
2
3
4

9. Funções no Plano Cartesiano
• Vamos aprender a reconhecer funções em um Plano Cartesiano.
x
y
x
y

10. Não é função pois a reta não
intercepta.
x
y
x
y
Não é função pois a reta
intercepta duas vezes.

11. Domínio, Contradomínio e Imagem
• Domínio – O conjunto de elementos de A que se
relacionam com B.
• Contradomínio – O conjunto de Chegada.
• Imagem – O conjunto de elementos de B que se
relacionam com A.
A B
Im
CDD

12. Domínio e Imagem
• Vamos aprender a reconhecer a Imagem e o Domínio no plano cartesiano.
x
y
-1
1
3
4
Im = { y ϵ R І 1 ≤ y ≤ 4 }
ou
Im = { y ϵ R І 4 ≥ y ≥ 1 }
D = { x ϵ R І -1 ≤ y ≤ 3 }
ou
D = { y ϵ R І 3 ≥ y ≥ -1 }

13. Função Sobrejetora
Quando a Imagem for igual ao Contradominio, teremos uma função
Sobrejetora.
A B A B A B
Não é
Sobrejetora
É Sobrejetora É Sobrejetora
Dica: se sobra não é Sobrejetora

14. Função Injetora
Quando todo elemento de A se corresponder com um elemento diferente em
B teremos uma função Injetora.
A B A B A B
Não é InjetoraÉ Injetora É Injetora
Dica: se tem traição não é Injetora.

15. Função Bijetora
Quando tivermos uma função que ao mesmo tempo é injetora e sobrejetora
ela será um função Bijetora.
A B A B A B
Não é
Bijetora
É Bijetora
Dica: se tem traição não é Injetora.
Não é
Bijetora

16. Leis de Formação
Uma função (quando possível) pode ser representada através de uma Lei de Formação, ou
seja, uma fórmula.
• Exemplo: f (x) = x + 3
f (1) = 1 + 3 = 4
Ou seja, quando x vale 1, o y vale 4.
Obs.: f(x) = y

17. Outros Tipos de Funções
x
y
Função
Crescente
x
y
x
y
Função
Decrescente
Função
Constante

18. Função Par e Função Impar
Função Par : Quando f (x) = f (-x) simetria em relação ao eixo y.
Função Impar: f(-x) = f - (x) simetria em relação ao seu ponto de origem.
x
y
x
y
Função Par Função Impar