Guia de Matemática para Pré-Vestibular

PRÉ-VESTIBULAR
LIVRO DO PROFESSOR
MATEMÁTICA
Esse material é parte integrante do Aulas Particulares on-line do IESDE BRASIL S/A,
mais informações www.aulasparticularesiesde.com.br

© 2006-2009 – IESDE Brasil S.A. É proibida a reprodução, mesmo parcial, por qualquer processo, sem autorização por escrito dos autores e do
detentor dos direitos autorais.
Produção
Projeto e
Desenvolvimento Pedagógico
Disciplinas Autores
Língua Portuguesa Francis Madeira da S. Sales
Márcio F. Santiago Calixto
Rita de Fátima Bezerra
Literatura Fábio D’Ávila
Danton Pedro dos Santos
Matemática Feres Fares
Haroldo Costa Silva Filho
Jayme Andrade Neto
Renato Caldas Madeira
Rodrigo Piracicaba Costa
Física Cleber Ribeiro
Marco Antonio Noronha
Vitor M. Saquette
Química Edson Costa P. da Cruz
Fernanda Barbosa
Biologia Fernando Pimentel
Hélio Apostolo
Rogério Fernandes
História Jefferson dos Santos da Silva
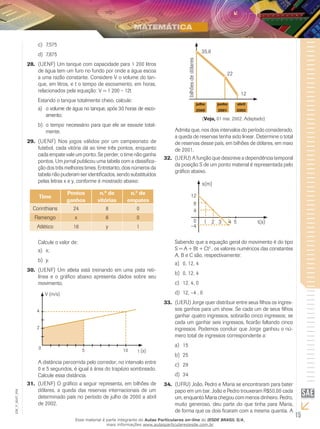
Marcelo Piccinini
Rafael F. de Menezes
Rogério de Sousa Gonçalves
Vanessa Silva
Geografia Duarte A. R. Vieira
Enilson F. Venâncio
Felipe Silveira de Souza
Fernando Mousquer
I229 IESDE Brasil S.A. / Pré-vestibular / IESDE Brasil S.A. —
Curitiba : IESDE Brasil S.A., 2009. [Livro do Professor]
660 p.
ISBN: 978-85-387-0571-0
1. Pré-vestibular. 2. Educação. 3. Estudo e Ensino. I. Título.
CDD 370.71

1
EM_V_MAT_004
Funções: Função
Afim, Função
Inversa e Função
Composta
Funções
Pode-se entender uma função como um dispo-
sitivo que responde a perguntas com duas caracte-
rísticas especiais: toda pergunta tem resposta e a
resposta a cada pergunta é única.
Isso faz com que as funções sejam amplamente
utilizadas tanto em Matemática como em outras ciên-
cias, pois permitem representar por meio de números
os fenômenos observados em experimentos.
Definição: Seja f uma relação de A em B, isto é,
f ⊂ A x B, dizemos que f é uma função de A em B se,
e somente se, para todo elemento x ∈ A existir um só
elemento y ∈ B, tal que (x, y) ∈ f, ou seja, y = f (x).
Portanto, para que uma relação de A em B seja
uma função, exige-se que a cada x ∈ A esteja asso-
ciado um único y ∈ B.
Entretanto, pode existir y ∈ B que não este-
ja associado a nenhum elemento pertencente ao
conjunto A ou que esteja associado a mais de um
elemento de A.
Os dois diagramas seguintes representam
relações de A em B, mas não funções de A em B. O
primeiro porque existe um elemento de A que não
está associado a nenhum elemento de B, e o segundo
porque existe um elemento de A que está associado
a mais de um elemento de B.
A
Bfa
b
c
d
e
f
A
Bfa
b
c
d
e
f
O diagrama de flechas a seguir representa uma
relação de A em B que também é uma função de A
em B:
A
B
fa
b
c
d
e
f
Domínio de f: D (f) = A
Contradomínio de f: B
Imagem de f: Im(f) ⊂ B
O domínio de f é o conjunto dos elementos de
A que são os primeiros termos dos pares ordenados
ou o conjunto origem das flechas.

2
EM_V_MAT_004
O conjunto B é chamado contradomínio de f
que são os segundos termos dos pares ordenados
do produto cartesiano ou o conjunto dos possíveis
destinos das flechas.
O conjunto imagem é um subconjunto de B
formado pelos elementos que são segundos termos
dos pares ordenados da função ou o conjunto dos ele-
mentos que são efetivamente destino de flechas.
No diagrama acima deve-se observar que de
todo elemento do conjunto A deve partir exatamente
uma flecha. Já os elementos do conjunto B podem
receber uma ou mais flechas ou até não receber
nenhuma flecha.
Notação:
f: A → B ou f = {(x , y)∈AxB  y = f (x)}
x → f(x)
Chamam-se funções reais de variável real,
aquelas cujo domínio e contradomínio são subcon-
juntos dos reais.
Nesse caso, costuma-se definir a função apenas
pela “regra de correspondência” e adota-se como
domínio o maior subconjunto possível de R.
As funções reais de variável real podem ser
representadas graficamente no plano cartesiano or-
togonal. O gráfico da função é composto por todos
os pares ordenados que compõem a função.
Em virtude da definição de função, toda reta
vertical, que passa por um ponto do domínio, in-
tercepta o gráfico da função em exatamente um
ponto.
A análise do gráfico da função permite identi-
ficar o seu domínio e a sua imagem, como pode ser
visto a seguir:
Zero ou raiz da função é o número x, cuja ima-
gem é nula, isto é, f(x) = 0. Esses pontos são identi-
ficados como os pontos onde o gráfico intercepta o
eixo das abscissas (Ox).
É possível, também, identificar o sinal da função
em cada trecho do domínio. Os pontos de imagem
positiva encontram-se acima do eixo das abscissas
(parte positiva do eixo das ordenadas) e os de ima-
gem negativa abaixo (parte negativa do eixo das
ordenadas).
– – 1 2 4 7
y = f (x)
x–
++ +
Funções iguais
Duas funções f e g são iguais se, e somente se,
tiverem o mesmo domínio, e f(x) = g(x) para todo
x no domínio. Isso é equivalente a dizer que todos
os pares ordenados que compõem as funções são
iguais.
Funções monotônicas
Chama-se monotônica ou monótona a função que
é sempre crescente ou decrescente no seu domínio.
Seja a função f: A → B
f é1) crescente (não-decrescente) se ∀ x, y ∈
A, tais que x < y ⇒ f (x) ≤ f (y).
f é2) decrescente (não-crescente) se ∀ x, y ∈
A, tais que x < y ⇒ f (x) ≥ f (y).
f é3) estritamente crescente (crescente) se ∀
x, y ∈ A, tais que x < y ⇒ f (x) < f (y).
f é4) estritamente decrescente (decrescente)
se ∀ x, y ∈ A, tais que x < y ⇒ f (x) > f (y).
São funções crescentes f(x) = 3x – 1, f(x) = 2x
e f(x) = x3
.
São funções decrescentes f(x)=–2x + 5, f(x) =
(1/2)x
e f(x) = –x3
.
As funções f(x) = x2
e f(x) = sen x não são cres-
centes e nem decrescentes em R.
Esses conceitos acima mencionados são facil-
mente notados no gráfico da função. Nas funções
crescentes o gráfico “sobe” para a direita, enquanto
nas funções decrescentes o gráfico desce para a
direita.

3
EM_V_MAT_004
yy
x x00
Já a função a seguir não é monótona, pois é
decrescente numa parte do domínio e crescente em
outra.
y
x0
Paridade
Seja A um conjunto tal que x ∈ A ⇒ −x ∈ A e
a função f: A → B
f é par ⇔ f(–x) = f(x), ∀x ∈ A → o gráfico é
simétrico em relação ao eixo Oy, pois (x, y) ∈ f ⇔
(–x, y) ∈ f.
f é ímpar ⇔ f(–x) = –f(x), ∀x ∈ A → o gráfico
é simétrico em relação à origem, pois (x,y) ∈ f ⇔
(–x,–y) ∈ f.
Se uma função não é nem par nem ímpar, dize-
mos que ela não possui paridade.
São funções pares f(x) = x2
e f(x) = cos x. São
funções ímpares f(x) = x3
e f(x) = sen x. A função f(x)
= x2
+ x – 1 não é par nem ímpar.
Abaixo são mostrados gráficos desses dois tipos
de funções:
y
x
0
y
x0
f(x) = x2
→ par
f(x) = sen x → ímpar
Tipologia das funções
Sejam a função f: A → B
f é sobrejetora quando todo elemento de B está
associado por f a pelo menos um elemento de A, ou
seja, quando a imagem é igual ao contradomínio. No
diagrama, todo elemento recebe seta. No gráfico,
retas horizontais traçadas no contradomínio inter-
ceptam o gráfico em pelo menos um ponto. n(A) ≥
n(B), se A e B forem finitos.
f é sobrejetora ⇔ ∀ y ∈ B, ∃ x ∈ A tal que (x, y)
∈ f ou y = f (x)
f é injetora quando elementos distintos de A
estão associados a elementos distintos de B. No
diagrama, não há elemento em B que receba mais
de uma seta. No gráfico, retas horizontais cruzam
seu gráfico em no máximo um ponto. n(A) ≤ n(B), se
A e B forem finitos.
f é injetora ⇔ ∀ x1
, x2
∈ A, x1
≠ x2
⇒ f (x1
) ≠ f
(x2
) ou ∀ x1
, x2
∈ A, f (x1
) = f (x2
) ⇒ x1
= x2
f é bijetora se, e somente se, for sobrejetora e
injetora. Todo elemento de B está associado por f a
um único elemento de A. No diagrama, todo elemento
de B recebe uma seta. No gráfico, retas horizontais
traçadas pelo contradomínio cruzam o gráfico em
exatamente um ponto. n(A) = n(B), se A e B forem
finitos.
Os diagramas de flechas abaixo exemplificam
essas definições:
1) Sobrejetora
a
b
c
A B
f
d
e
2) Injetora
a
b
c
A B
d
e
f
g
f

4
EM_V_MAT_004
3) Bijetora
a
b
c
A B
d
e
f
f
Função limitada
A função f é limitada se ∃ K > 0, tal que ∀ x ∈
D (f) ⇒f (x)  < K.
A função f(x) = sen x é uma função limitada,
pois ∀x ∈ R, –1 ≤ sen x ≤ 1. A função f(x) = x2
não é
limitada, pois ∀ k > 0, ∃ x, tal que f(x) = x2
> k.
Função periódica
A função f é periódica ⇔ ∃ p > 0 tal que f (x) = f(x
+ p), ∀x ∈ D (f).
Isso significa que os valores da função se repe-
tem em intervalos de tamanho p.
O menor número positivo p é chamado período
da função.
Os exemplos mais comuns de funções perió-
dicas são as funções trigonométricas. A função f(x)
= sen x, por exemplo, é uma função periódica de
período 2π.
Função definida por várias
sentenças abertas
Uma função f pode ser definida por várias sen-
tenças abertas, cada uma das quais ligada a um
domínio Di
contido no domínio de f.
Exemplo:``





≥
<≤
<
=→
1xpara1
1x0para2
0xpara1
f(x)quetalRRf:
Função constante
É a função que assume o mesmo valor em todo
o seu domínio.
f (x) = c, ∀ x ∈ D(f)
O gráfico de uma função constante com domínio
nos reais é uma reta paralela ao eixo dos x (horizon-
tal) e passando pelo ponto (0, c). Sua imagem é o
conjunto Im = {c}.
Exemplo:``
f(x) = 5 e f(x) = –3
y
x
(0, c)
0
No estudo das funções, muitas vezes é neces-
sário saber que valor do domínio leva a determinado
resultado na imagem. A função inversa associa os
valores da imagem aos do domínio.
Novamente, pensando na função como um
dispositivo que responde a perguntas, a função
inversa poderia ser entendida como um dispositivo
que informa qual a pergunta, dado que a resposta
é conhecida.
A função composta também é de grande impor-
tância, pois diversos processos ocorrem por meio da
aplicação sucessiva de funções. A função composta
permite identificar o resultado dessas diversas fun-
ções como se fossem uma única função.
Função composta
Dados os conjuntos A, B e C e as funções f: A →
B definida por y = f (x) e g: B → C definida por z = g
(y), chama-se função composta de g com f a função
h = (g o f) : A → C, definida por:
z = (g o f) (x) = g (f (x))
Assim, a função (gof) pode ser entendida como
uma função única que apresenta o mesmo resultado
que as aplicações sucessivas de f e g.
A função (gof) só é definida quando a imagem
de f está contida no domínio de g.
Os conceitos acima podem ser melhor entendi-
dos observando-se o diagrama de flechas a seguir:

5
EM_V_MAT_004
2 •
3 •
4 •
1 •
2 •
3 •
4 •
• 0
• 2
• 4
• 6
• 8
A
B
C
f
g
h = gof
A composição de funções não é comutativa: g o
f ≠ f o g. Pode acontecer também que somente uma
das funções (fog) ou (gof) esteja definida.
A sentença aberta que define (gof) (x) = g (f (x))
é obtida de g(x) substituindo-se x pela expressão
de f (x).
Exemplo:``
Sejam as funções reais f(x) = x2
+ 4x – 5 e g(x) = 2x – 3.
As expressões de (fog) e (gof) podem ser calculadas
como segue:
(fog) (x) = f(g(x)) = f (2x – 3) = (2x – 3)2
+4⋅(2x – 3)
– 5 = 4x2
– 4x – 8
(gof) (x) = g(f(x) = g(x2
+ 4x – 5) = 2 . ( x2
– 4x – 5) – 3
= 2x2
+ 8x – 13
Função inversa
Se f é uma função bijetora de A em B, a relação
inversa de f é uma função de B em A chamada função
inversa de f e denotada por f-1
e também é bijetora.
(x , y) ∈ f ⇔ (y , x) ∈ f – 1
Uma função só possui inversa se ela for bi-
jetora.
A função inversa é composta pelos pares orde-
nados obtidos pela inversão da ordem dos elementos
dos pares ordenados da função original. Assim, se a
função f: A → B associa cada elemento x ∈ A a um
elemento correspondente y ∈ B, a função f-1
, inversa
de f, associa a cada elemento y ∈ B o elemento cor-
respondente x ∈ A.
O domínio da função inversa é a imagem da
função original e a imagem da função inversa é o
domínio da função original.
D (f – 1
) = Im (f) e Im (f – 1
) = D (f)
Esses conceitos podem ser observados nos
diagramas de flecha seguintes:
a
b
c
d
e
f
d
e
f
a
b
c
A B B A
f f-1
As relações a seguir também são úteis:
1.ª) (f-1
) -1
= f
2.ª) ∀ x ∈ A, f-1
(f (x)) = x
3.ª) ∀ x ∈ B, f (f-1
(x)) = x
A primeira significa que a função inversa da
função inversa é igual à função original.
A segunda e terceira relações significam que
a composição entre a inversa e a função em qual-
quer ordem é a função identidade, ou seja, resulta
no elemento sobre o qual a função foi aplicada.
Os gráficos de f e f-1
são simétricos em relação
à bissetriz dos quadrantes ímpares (B13
), como pode
ser visto no exemplo abaixo:
• –8(–2; –8)
•
•
•
y
8
2
1–2–8
–2
–1 2 8 x
(8; 2)
(2; 8)
(–8; –2)
bissetrizf: y = x3
3
xy:3–f =
Obtenção da expressão da
função inversa
1.º Método:
Na sentença y = f(x), trocamos x por y e y por
x, obtendo x = f(y).
Em seguida, expressamos y em função de x,
transformando algebricamente a expressão x = f (y)
em y = f-1
(x).
Exemplo:``
A função inversa da função bijetora f: R →→ R, definida
por y = 2x – 4 pode ser calculada utilizando a regra
prática:

6
EM_V_MAT_004
1.º) permutar as variáveis: x = 2y – 4
2.º) expressar y em função de x: x = 2y – 4 ⇒ 2y = x +
4 ⇒ y = x + 4 .
2
A função inversa é então f −1
: R→R, definida por ⇒
y =
x + 4
.
2
2.º Método:
Basta utilizar a expressão vista anteriormente f
(f−1
(x)) = x e então obter a expressão de f−1
(x).
Exemplo:``
A função inversa da função bijetora f: → , definida por
y = 2x – 4 também pode se calculada como segue:
f (f - 1
(x)) = x ↔ 2⋅( f -1
(x)) –4 = x ↔
2⋅( f−1
(x)) = x + 4 ↔f –1
(x) =
x + 4
2
Função identidade
É uma função de R em R que a cada elemento
x ∈ R associa o próprio x.
f (x) = x , ∀ x ∈ R
O gráfico da função identidade é a bissetriz dos
quadrantes ímpares (β13
) e sua imagem é o conjunto
dos números reais: Im = R.
y
x
(2; 2)
(1; 1)
(0; 0)
(–1; –1)
(–2; –2)
Função linear
É uma função de R em R que a cada elemento x
∈ R associa o elemento ax ∈ R com a ≠ 0
f (x) = a ⋅ x , a ≠ 0
O gráfico da função linear é uma reta que passa
pela origem e sua imagem é o conjunto dos números
reais: Im = R.
(1; 2)
(0; 0)
2
1
y
x
A função f(x) =ax, com a > 0 e definida de R+
em
R+
é umarestriçãodafunçãolinearquerepresenta uma
proporcionalidade.
Sendo f(x1
) = y1
e f(x2
) = y2
, pode-se escrever
A relação acima é chamada de proporção, as
grandezas x e y são ditas diretamente proporcionais e
o coeficiente a é chamado fator de proporcionalidade.
Um exemplo comum é a massa de um corpo
que é proporcional ao seu volume e a relação entre
eles é o fator de proporcionalidade chamado massa
específica (ou densidade).
Função afim
É uma função de R em R definida por
f (x) = ax + b
onde a e b são constantes reais e a ≠ 0.
A função identidade (a = 1 e b = 0) e a fun-
ção linear (b = 0) são casos particulares da função
afim.
A função afim é uma função polinomial do 1.º
grau, seu gráfico é uma reta não-paralela a nenhum
dos eixos coordenados e sua imagem é o conjunto
dos números reais: Im = R.
O coeficiente a é chamado coeficiente angular
e representa a taxa de variação média da função
∆
∆
y
x
que é igual à tangente do ângulo de inclinação
da reta. Sendo θ o ângulo de inclinação da reta,
tem-se
tg θ = a
a > 0 → θ é agudo → função crescente
a < 0 → θ é obtuso → função decrescente
O coeficiente b é chamado coeficiente linear e
é o ponto onde a reta intercepta o eixo Oy, ou seja,
a reta passa no ponto (0, b).

7
EM_V_MAT_004
O gráfico intercepta o eixo dos x em um único
ponto que é a raiz da equação f(x) = 0 dada por x
= −b/a.
Abaixo são mostrados gráficos da função afim
para a negativo e positivo.
•
•
y = ax +b
a > 0
b
–b/a x
y
θ
•
x
y
θ
•
θ
x1
x2
•
y
θ
•
x-b/a
b
y = ax + b
a < 0
y
θ
x
θ
Dx
Dy
Dx

Dy

Sinais da função afim
Conhecendo o gráfico da função afim pode-se
realizar o seu estudo de sinais, isto é, identificar o
sinal da função em cada trecho do seu domínio, como
representado nas figuras seguintes:
•
y > 0
y < 0
y
x
Caso a > 0
)
a
b
–(x <
)
a
b
–(x <
)
a
b
–(x >
•
y > 0
y < 0
y
x
Caso a < 0
)
a
b
–(x <
)
a
b
–(x <
)
a
b
–(x >
Posições relativas entre retas
A análise dos coeficientes angulares das retas
permite identificar a posição relativa entre as retas.
Assim, sejam a reta r dada pela equação y = ax
+b e a reta s dada pela equação y = a’x +b’, a relação
entre seus gráficos é mostrada abaixo:
a = a’ e b ≠ b’ → retas paralelas
a = a’ e b = b’ → retas coincidentes
a ≠ a’ → retas concorrentes
a.a’ = −1 → retas perpendiculares
Isso permite também discutir sistemas de equa-
ções do primeiro grau a duas variáveis.
(PUC-SP) Qual dos gráficos seguintes representa uma1.
função de +
* em ?
a)
b)
c)

8
EM_V_MAT_004
d)
e)
Solução:`` C
O gráfico da letra a representa uma função de em +
*.
O gráfico da letra b também representa uma função de
em +
*.
O gráfico da letra c representa uma função de +
* em
.
O gráfico da letra d representa uma função de em +
.
O gráfico da letra e não representa uma função.
(FUVEST-SP)2. A figura abaixo representa o gráfico de
uma função da forma 3.x1–para
cbx
ax
f(x) ≤≤
+
+
= 3.x1–para
cbx
ax
f(x) ≤≤
+
+
=
•
•
•
•
•
y
x
– 1
– 1
– 3
1
2 3
1/5
–1/3
Pode-se concluir que o valor de b é:
-2a)
-1b)
0c)
1d)
2e)
Solução:`` D
A análise do gráfico mostra que os pontos (–1, – 3); (0, –1)
e (2, 0) pertencem à função. Assim,
2 a
f ( 2,0 ) 0 a 2
b.2 c
0 a
f (0, 1) 1 c 2
b.0 c
1 2
f ( 1, 3 ) 3 b 1
b.( 1) 2
+
= = ⇒ = −
+
+
− = = − ⇒ =
+
− −
− − = = − ⇒ =
− +
(PUC-RS) O domínio da função real dada por3.
4–x
x1
f(x)
+
=
é:
{xa) ∈Rx > –1 e x < 4}
{xb) ∈Rx < –1 ou x ≥ 4}
{xc) ∈Rx ≥ –1 e x ≤ 4}
{xd) ∈Rx ≤ –1 ou x > 4}
{xe) ∈Rx ≥ –1 e x < 4}
Solução:`` D
O domínio da função é o maior subconjunto dos reais
para o qual a função é definida. Nesse caso, a expressão,
sobre a raiz de índice par, deve ser não-negativa e o
denominador não pode ser nulo.
O diagrama a seguir mostra a variação do espaço em4.
função do tempo referente a um ponto material. De-
termine:
t (s)
S (m)
6
4
0 2 6 8
o espaço inicial do movimento;a)
o instante em que o ponto material atinge ob)
marco zero;
o intervalo de tempo durante o qual a veoci-c)
dade do móvel é positiva;
o intervalo de tempo durante o qual a veloci-d)
dade do móvel é negativa;
o intervalo de tempo durante o qual o móvele)
se encontra em repouso.

9
EM_V_MAT_004
Solução:``
O espaço inicial é a posição em t = 0s, ou seja,a)
s(0)= 4 m.
O instante no qual a posição do ponto material éb)
zero, o que ocorre quando t = 8 s.
Velocidade do móvel é positiva quando o espaçoc)
aumenta com o tempo, ou seja, quando a função é
crescente; isso ocorre entre 0 s e 2 s.
A velocidade do móvel é negativa quando o espaçod)
diminui com o tempo, ou seja, quando a função é
crescente; isso ocorre entre 0 s e 2 s.
O móvel está em repouso quando o valor do espaçoe)
não se altera, isto é, quando a função permanece
constante; isso ocorre entre 2 s e 6 s.
(PUC SP) Se5.
x–1
1
f(x)= , então (fo(fof)) (x) é igual a:
2xa)
3xb)
4xc)
xd)
-xe)
Solução:`` D
(fo (fof) (x) = f (f (f (x) ) ) = f (f (
1
1 – x
) )=
f
1
1
1-
1 - x
=
f (
1 – x
– x
) = 1
1 – x
– x
= x
1-
(CESGRANRIO) Seja f: x6. → f(x) a função cujo grá-
fico é:
y
0 x
O gráfico que mais bem representa a função inversa
f−1
: x → f−1
(x) é:
a)
x
y
0
b)
y
0 x
c)
y
x0
d)
x
y
0
e)
y
x0
Solução:`` E
Basta observarmos o gráfico da função original e procurar
dentre as opções um gráfico que seja simétrico a ele em
relação à bissetriz dos quadrantes ímpares.
O melhor gráfico é o da opção E.
A função c (x) = 5.7.
x – 32
9 pode ser usada para a
conversão de uma temperatura x na escala Fahrenheit para
uma temperatura na escala Celsius. A função k (x) = x +
273podeserutilizadaparaaconversãodeumatemperatura
x na escala Celsius para uma temperatura na escala Kelvin.
Obtenha uma expressão para a conversão direta da escala
Fahrenheit para a escala Kelvin. Qual a temperatura em que
essas duas escalas fornecem o mesmo valor numérico?
Solução:``
Basta efetuar a composição das funções.
K(c(x)) = K 5.
x – 32
9
= 5.
x – 32
9
+ 273 =
5x + 2297
9
Para que as duas temperaturas sejam iguais, devemos
fazer
K(c(x)) = x ⇒ 5x + 2297
9
= x ⇒ x = 547,25° F = 547,25 k
(UERJ-1998) A promoção de uma mercadoria em um8.
supermercado está representada, no gráfico abaixo, por
seis pontos de uma mesma reta.

10
EM_V_MAT_004
•
•
•
•
•
•
150
50
5 20 30 quantidade de unidades
compradas
valor total da compra (R$)
Quem comprar 20 unidades dessa mercadoria,
na promoção, pagará por unidade, em reais, o
equivalente a:
4,50a)
5,00b)
5,50c)
6,00d)
Solução:`` A
O valor total da compra f(x) está associado à quantidade
de unidades compradas x por uma reta. Assim,
f(x) = ax + b
Os pontos (5, 150) e (30, 50) pertencem à reta, então
f(5) = 150 ⇒ 5a + b = 150
f(30) = 50 ⇒ 30a + b = 50
Subtraindo a primeira equação da segunda:
25a = –100 ⇔ a = –4
5 (–4) + b = 150 ⇔ b = 170
Logo, f(x) = –4x + 170
Numa compra de 20 unidades, tem-se x = 20 e o valor da
compra f(20) = –4 ⋅ 20 + 170 = 90. O valor por unidade
será então 90/20 = 4,5.
(UNICAMP 1992) Calcule a e b positivos na equação9.
da reta ax + by = 6 de modo que ela passe pelo ponto
(3, 1) e forme com os eixos coordenados um triângulo
de área igual a 6.
Solução:`` a = 1 e b = 3.
Os pontos onde a reta intercepta os eixos coordenados
são os pontos para os quais x = 0 e y = 0.
x = 0 ⇒ a ⋅ 0 + by = 6 ⇒ y = 6/b
y = 0 ⇒ ax + b ⋅ 0 = 6 ⇒ x = 6/a
Como mostrado no gráfico a seguir.
a
6
b
6
0 x
y
A área do triângulo é 6
2
a
6.
b
6
= , logo a ⋅ b = 3.
A reta passa pelo ponto (3, 1), daí 3a + b = 6 ⇒ b =
6 – 3a
Substituindo a expressão de b na equação anterior.
a⋅(6 – 3a) = 3 ⇒ a2
– 2a + 1 = 0 ⇒ ⇒ a = 1 e
b = 6 – 3 ⋅ 1 = 3
(UFJF 2000) O esboço de gráfico abaixo mostra a tem-10.
peratura de uma região de 3h da madrugada até às 9h
da manhã do mesmo dia.
y
x
3
–5
10
0 9
Determine o horário em que a temperatura atingiua)
0º C.
Determine o tempo em que a temperatura perma-b)
neceu negativa.
Determine o tempo em que a temperatura perma-c)
neceu positiva.
Solução:``
A reta passa pelos pontos (3, –5) e (9, 10). Supondoa)
que a equação da reta seja f(x) = ax + b, tem-se:
f(3) = 3a + b = –5
f(9) = 9a + b = 10
Fazendo a segunda equação menos a primeira.
6a = 15 ⇒ a =
5
2
3 ⋅ (5/2) + b = –5 ⇒ b = – 25
2
Logo, f (x) =
5
2
x –
25
2

11
EM_V_MAT_004
O horário em que a temperatura atingiu 0º C é o
valor de x tal que f(x) = 0.
f (x) =
5
2
x –
25
2
= 0 ⇒ x = 5
Logo, a temperatura atingiu 0ºC às 5h.
A temperatura permaneceu negativa para 3b) ≤ x < 5,
ou seja, durante 2h.
A temperatura permaneceu positiva para 5 < xc) ≤ 9,
ou seja, durante 4h.
(UNICAMP - 1999) A troposfera, que é a primeira11.
camada da atmosfera, estende-se do nível do mar até a
altitude de 40 000 pés; nela, a temperatura diminui 2º C
a cada aumento de 1 000 pés na altitude. Suponha que
em um ponto A, situado ao nível do mar, a temperatura
seja de 20ºC. Pergunta-se:
Em que altitude, acima do ponto A, a temperaturaa)
é de 0ºC?
Qual é a temperatura a 35 000 pés acima do mesmob)
ponto A?
Solução:``
Como a taxa de variação é constante, a temperatura f(x)
pode ser relacionada com a altura x por uma função do
1º grau.
f(x) = ax + b
temperatura ao nível do mar é 20ºC ⇒ f(0) = b = 20 a
temperatura diminui 2º a cada aumento de 1 000 pés:
⇒ a =
∆y
∆x
=
–2
1000 =
–1
500
Logo, f (x)
–x
500 + 20
Deve-se encontrar x tal que f(x) = 0a)

f (x)
–x
500
+ 20 = 0 ⇒
–x
500
= –20 ⇒ x = 10 000
Resposta: A temperatura é de 0ºC a 10 000 pés.
Deve-se obter o valor da função para x = 35 000b)
f (35000) = –35 000
500
+ 20 = –50
A temperatura é –50ºC.
(UERJ) Em uma partida, Vasco e Flamengo levaram1.
ao Maracanã 90 000 torcedores. Três portões foram
abertos às 12 horas e até as 15 horas entrou um número
constante de pessoas por minuto. A partir desse horário,
abriram-se mais três portões e o fluxo constante de
pessoas aumentou. Os pontos que definem o número
de pessoas dentro do estádio em função do horário de
entrada estão contidos no gráfico abaixo:
12 15 17 horário
n.° de pessoas
45 000
30 000
90 000
Quando o número de torcedores atingiu 45 000, o
relógio estava marcando 15 horas e:
20min.a)
30min.b)
40min.c)
50min.d)
(UERJ) A estatura de um adulto do sexo feminino pode2.
ser estimada, através das alturas de seus pais, pela
expressão:
(y - 13) + x
2
Considere que x é a altura da mãe e y a do pai, em cm.
Somando-se ou subtraindo-se 8,5cm da altura estimada,
obtém-se, respectivamente, as alturas máxima ou mínima
que a filha adulta pode atingir. Segundo essa fórmula, se
João tem 1,72m de altura e sua esposa tem 1,64m, sua
filha medirá, no máximo:
1,70ma)
1,71mb)
1,72mc)
1,73md)
(UERJ) A velocidade angular W de um móvel é inversa-3.
mente proporcional ao tempo T e pode ser representada
pelo gráfico abaixo.
2
w (radianos/segundo)
0,5
T (segundo)

12
EM_V_MAT_004
Quando W é igual a 0,8π rad/s, T, em segundos, cor-
responde a:
2,1a)
2,3b)
2,5c)
2,7d)
(UERJ) Uma panela, contendo um bloco de gelo a −40º4.
C, é colocada sobre a chama de um fogão. A evolução
da temperatura T, em graus Celsius, ao longo do tempo
x, em minutos, é descrita pela seguinte função real:
20x – 40 se 0 ≤ x < 2
0 se 2 ≤ x ≤ 10
10x – 100 se 10 < x ≤ 20
100 se 20 < x ≤ 40
T(x) =
O tempo necessário para que a temperatura da água
atinja 50º C, em minutos, equivale a:
4,5a)
9,0b)
15,0c)
30,0d)
(UFRJ 2002) Considere as funções polinomiais5. f, g e h,
cujos gráficos são dados a seguir.
x
–5 –3 –2 –1
–4
y
0
1 2 3
4 5
–2
–4
–6
2
4
6
h
f
g
Determine os valores reais de x no intervalo [-5, 5] para
os quais valem as desigualdades: f(x) ≤ g(x) ≤ h(x).
(UFRJ) Dada a função f: R6. → R definida por:
x3
– 4x se x ≤1
2x – 5 se x > 1
f(x) =
determine os zeros de f.
(PUC-RJ) A função7. :
é sempre positiva.a)
pode assumir qualquer valor real.b)
pode assumir o valor 1/3.c)
pode assumir o valor −1/6.d)
pode assumir o valor 1/2.e)
(PUC-RJ) Dada a função f(x) = (x + 1)⋅(x8. 2
– x + 1), deter-
mine:
f(−1) e f(0)a)
Ache as soluções reais da equação f(x) = 9b)
(U9. FF) Determine o domínio da função real da variável
real f, definida por f(x) =
x2
- 4x + 3
4
x - 1
(10. UFF) Classifique cada afirmativa abaixo, em verdadeira
ou falsa, justificando.
∀( )( x ∈ R, x < 0, -x sempre existe em R.
∀( )( x ∈ R, log (–x) não existe em R.
∀( )( x ∈ R, se (x – a)2
= (x – b)2
então a = b.
∀( )( x ∈ R, 2–x
< 0.
∀( )( x ∈ R, sen x ≤ 1.
(UFF) Considere o11. polinômio p(x) = x3
– 3x + 2 e a fun-
ção real de variável real f definida por .
Sabe-se que uma das raízes de p(x) é 1. Escreva o
domínio de f sob a forma de intervalo.
(UFF) O gráfico da função f está representado na figura:12.
Sobre a função f é falso afirmar que:
f(1) + f(2) = f(3)a)
f(2) = f(7)b)
f(3) = 3f(1)c)
f(4) – f(3) = f(1)d)
f(2) + f(3) = f(5)e)
(UERJ) Nicole pediu a seu irmão João que pensasse13.
em um número e efetuasse as seguintes operações,
nesta ordem:
multiplicar o número pensado por 5;1.° )
adicionar 6 ao resultado;2.° )
multiplicar a soma obtida por 4;3.° )
adicionar 9 ao produto;4.° )
multiplicar a nova soma por 5.5.° )

13
EM_V_MAT_004
João comunicou que o resultado é igual a K.
As operações que Nicole deve efetuar com K, para
“adivinhar” o número pensado, equivalem às da seguinte
expressão:
(K – 165) : 100a)
(K – 75) : 100b)
K : 100 + 165c)
(K + 165) : 100d)
(UERJ) Considere a função f:14.
2
Determine suas raízes.a)
Calculeb)
(UFF) Considere as funções reais de variável real15. f e
g definidas por f(x) = 3x +1 e g(x) = −2x −2. Deter-
mine:
a função h = fog;a)
as inversas de f e g.b)
(UFF) Considere as funções reais bijetivas16. f e g tais
que:
x f(x) g(x)
−1 1 2
0 2 1
1 0 −1
2 −1 0
Determine, justificando, os valores de:
(f o g) (1)a)
(g o fb) –1
) (2)
(fc) –1
o g–1
) (-1)
(fd) –1
o g) (2)
(UFF) Dada a função real de variável real17. f tal que
f (2x + 1) =
x2
- 1
2x , x ≠ 1 e x ≠ –1, determine:
a expressão de f(x);a)
o domínio da função f.b)
(UFF) Sejam T: M18. → M e S: M → M as funções repre-
sentadas a seguir.
Com respeito à função composta ToS, tem-se:
ToS(3) = S(3)a)
ToS(1) = S(3)b)
ToS(3) = T(2)c)
ToS(2) = T(1)d)
ToS(4) = ToS(1)e)
(UFF) Dada a função real de variável real19. f, definida
por:
f(x) =
x + 1
x - 1
, x ≠ 1:
determine (fof) (x);a)
escreva uma expressão para fb) –1
(x).
(UFF) Considere20. f e g funções reais de variável real,
definidas por f(x) = e g (x) = log (1– x).
Determine o domínio de f.a)
Defina a inversa de g.b)
(UFCE) . Seja21. f uma função real de variável real definida
por f(x) = x2
+ c, c > 0 e c ∈ R, cujo gráfico é
y
x
(0, c)
x2
Então o gráfico que melhor representa f(x + 1) é:
a)
y
x

14
EM_V_MAT_004
b)
y
x
c)
y
x
d)
y
x
e)
y
x
(UNIRIO) Considere as funções:22.
f: R R
x y = x −3
g: R R
x y = 2x
h: R R
x y = x
Determine o conjunto-imagem da função fogoh.
(UNESP) Dadas as funções f(x) = x23. 2
+ 2x +1 e
g(x) = x −1,
encontre a função composta (fog) (x);a)
resolva a equação: (fog) (y) = 0, onde y = cos x.b)
(FATEC) Um pai dividiu a quantia de R$750,00 entre seus24.
três filhos. A quantia recebida por Carlos correspondeu
a 10/7 da recebida por André e esta correspondeu a
7/8 da recebida por Bruno. É verdade que:
Carlos recebeu R$60,00 a mais que Bruno.a)
André recebeu R$100,00 a menos que Carlos.b)
Bruno recebeu R$70,00 a menos que Carlos.c)
Carlos recebeu R$100,00 a mais que André.d)
André recebeu R$40,00 a menos que Bruno.e)
(UERJ) Em um restaurante há 12 mesas, todas ocupa-25.
das. Algumas, por quatro pessoas; outras, por apenas
duas pessoas, num total de 38 fregueses.
O número de mesas ocupadas por apenas duas pessoas
é:
4a)
5b)
6c)
7d)
(UERJ) O Real Enferrujou26.
“[...]asmoedasde1e5centavosoxidamantesdoprevisto
[...]Atéagora,apenas116milhõesentreossetebilhõesde
moedas em circulação têm nova roupagem lançada pelo
governo no dia 1.º julho [...]” (ISTOÉ, 09 set. 1998)
Desses 116 milhões de moedas, metade é de R$0,50,
a metade do número restante é de R$0,10, a metade
do que sobrou é de R$0,05 e as últimas moedas são
de R$0,01. O total de moedas de R$0,01 corresponde,
em reais, a:
14.500,00a)
29.000,00b)
145.000,00c)
290.000,00d)
(UERJ) Observe o gráfico:27.
ProductAudit/Expand.
Seoconsumodevinhobrancoalemão,entre1994e1998,
sofreuumdecréscimolinear,ovolumetotaldesseconsumo
em 1995, em milhões de litros, corresponde a:
6,585a)
6,955b)

15
EM_V_MAT_004
7,575c)
7,875d)
(UENF) Um tanque com capacidade para 1 200 litros28.
de água tem um furo no fundo por onde a água escoa
a uma razão constante. Considere V o volume do tan-
que, em litros, e t o tempo de escoamento, em horas,
relacionados pela equação: V = 1 200 – 12t
Estando o tanque totalmente cheio, calcule:
o volume de água no tanque, após 30 horas de esco-a)
amento;
o tempo necessário para que ele se esvazie total-b)
mente.
(UENF) Nos jogos válidos por um campeonato de29.
futebol, cada vitória dá ao time três pontos, enquanto
cada empate vale um ponto. Se perder, o time não ganha
pontos. Um jornal publicou uma tabela com a classifica-
ção dos três melhores times. Entretanto, dois números da
tabela não puderam ser identificados, sendo substituídos
pelas letras x e y, conforme é mostrado abaixo:
Time
Pontos
ganhos
n.º de
vitórias
n.º de
empates
Corinthians 24 8 0
Flamengo x 6 0
Atlético 16 y 1
Calcule o valor de:
x;a)
y.b)
(UENF) Um atleta está treinando em uma pista reti-30.
línea e o gráfico abaixo apresenta dados sobre seu
movimento.
4
2
V (m/s)
0 5 10 t (s)
A distância percorrida pelo corredor, no intervalo entre
0 e 5 segundos, é igual à área do trapézio sombreado.
Calcule essa distância.
(UENF) O gráfico a seguir representa, em bilhões de31.
dólares, a queda das reservas internacionais de um
determinado país no período de julho de 2000 a abril
de 2002.
35,6
22
12
bilhõesdedólares
julho
2000
junho
2001
abril
2002
(Veja, 01 mai. 2002. Adaptado)
Admita que, nos dois intervalos do período considerado,
a queda de reservas tenha sido linear. Determine o total
de reservas desse país, em bilhões de dólares, em maio
de 2001.
(UERJ) A função que descreve a dependência temporal32.
da posição S de um ponto material é representada pelo
gráfico abaixo.
s(m)
t(s)
12
8
4
0
–4
1 2 3 4 5
Sabendo que a equação geral do movimento é do tipo
S = A + Bt + Ct2
, os valores numéricos das constantes
A, B e C são, respectivamente:
0, 12, 4a)
0, 12, 4b)
12, 4, 0c)
12, –4 , 0d)
(UERJ) Jorge quer distribuir entre seus filhos os ingres-33.
sos ganhos para um show. Se cada um de seus filhos
ganhar quatro ingressos, sobrarão cinco ingressos; se
cada um ganhar seis ingressos, ficarão faltando cinco
ingressos. Podemos concluir que Jorge ganhou o nú-
mero total de ingressos correspondente a:
15a)
25b)
29c)
34d)
(UFRJ) João, Pedro e Maria se encontraram para bater34.
papo em um bar. João e Pedro trouxeram R$50,00 cada
um, enquanto Maria chegou com menos dinheiro. Pedro,
muito generoso, deu parte do que tinha para Maria,
de forma que os dois ficaram com a mesma quantia. A

16
EM_V_MAT_004
seguir, João resolveu também repartir o que tinha com
Maria, de modo que ambos ficassem com a mesma
quantia. No final, Pedro acabou com R$4,00 a menos
do que os outros dois. Determine quanto Maria possuía
quando chegou ao encontro.
(PUC-RJ) João dá a Pedro tantos reais quanto Pedro35.
possui. Em seguida, Pedro dá a João tantos reais quanto
João possui. Se terminaram com R$180,00 cada um,
quantos reais cada um deles possuía inicialmente?
João possuía R$100,00 e Pedro R$80,00.a)
João possuía R$200,00 e Pedro R$225,00.b)
João possuía R$135,00 e Pedro R$280,00.c)
João possuía R$225,00 e Pedro R$135,00.d)
João possuía R$100,00 e Pedro R$135,00.e)
(UFF) Na figura a seguir estão representadas as retas36.
r e s.
Sabendo que a equação da reta s é x = 3 e que OP
mede 5 cm, a equação de r é:
y = 3/4xa)
y = 4/3xb)
y = 5/3xc)
y = 3 xd)
y = 5 xe)
(UFF) As empresas Alfa e Beta alugam televisores do37.
mesmo tipo. A empresa Alfa cobra R$35,00 fixos pelos
primeiros 30 dias de uso e R$1,00 por dia extra. A em-
presa Beta cobra R$15,00 pelos primeiros 20 dias de
uso e R$1,50 por dia extra. Após n dias o valor cobrado
pela empresa Beta passa a ser maior do que o cobrado
pela empresa Alfa. O valor de n é:
25a)
35b)
40c)
45d)
50e)
(UNIRIO) Saiu na Veja, em 2003 “A conta do GNV –38.
Quanto vale converter seu carro para o gás natural.
Calcule o gasto de combustível de seu carro por1)
quilômetro. Se ele faz 10km por litro de gasolina, e
o litro custa 2 reais, o gasto é de 20 centavos por
quilômetro.
A grosso modo, um metro cúbico de gás natural2)
rende quilometragem 20% superior à de 1 litro de
gasolina e 40% acima da obtida com 1 litro de álco-
ol. Portanto, com GNV o carro do item 1 fará 12 qui-
lômetros por metro cúbico a 1 real o metro cúbico,
esse veículo gastará 8 centavos por quilômetro.”
Se você pagar R$2.100,00 para fazer a conversão do
seu automóvel para GNV, a economia será feita a partir
da seguinte quilometragem.
18 000kma)
17 500kmb)
17 000kmc)
16 500kmd)
16 000kme)
(UERJ) Considere a função f, definida para todo x real1.
positivo, e seu respectivo gráfico.
y
x
0 a b 3a 3b
f(x) =
1
x
Se a e b são dois números positivos (a < b), a área
do retângulo de vértices (a,0), (b,0) e (b, f(b)) é igual
a 0,2.
Calcule a área do retângulo de vértices (3a, 0), (3b, 0)
e (3b, f(3b)).
(UFF) Determine o domínio da função de variável real2. f
definida por
−
=
−
2
(x 1)
1
f(x)
1 10
(UFJF) A figura a seguir representa, no plano cartesiano,3.
o gráfico de uma função y = f(x) definida no intervalo
[-2,5].

17
EM_V_MAT_004
Com base neste gráfico, é incorreto afirmar que:
y
4
3
2
1
0
–1
1 2 3 4 5
–1–2
x
f(4) > f(5).a)
o conjunto imagem de f contém o intervalo [−1, 4].b)
f(x) < 0 se −2c) ≤ x ≤ 0.
f(f(1)) = 0.d)
o conjunto {xe) ∈ [−2, 5]  f(x) = 3} possui exata-
mente dois elementos.
(UNIRIO)Considereafunçãorealf:A4. →R,ondeRdenota
o conjunto dos números reais, cujo gráfico é apresentado
a seguir, sendo o eixo das ordenadas e a reta de equação
y = 3, assíntotas da curva que representa f : x → y =
f(x).
y
x
3
0
Determine o domínio e o conjunto-imagem de f.a)
Esboce o gráfico da função g: Bb) → R; x → y = f(x
−2) −4
(UNIRIO) Seja f a função real na variável x definida por5.
+ −
=
+ − −
1 x + 1 x
f(x)
1 x 1 x
Determine o domínio de definição D da função.a)
Mostre que, para todo xb) ∈ D, tem-se
+ +
=
+
2
1 1 x
f(x)
1 x
(UFF) Considere a função real de variável real f e a fun-6.
ção g tal que Dom(g) = [–1,4] e g (x) = f (2x) – 1.
O gráfico de g é representado na figura a seguir.
Pede-se:
a expressão que define g;a)
a imagem de g;b)
a expressão que define f no intervalo [0,4].c)
(UFF) Para a função f: N*7. → N*, que a cada número
natural não-nulo associa o seu número de divisores
positivos, considere as afirmativas:
existe um natural não-nulo n tal que f(n) = n.I.
f é crescente.II.
f não é injetiva.III.
Assinale a opção que contém a(s) afirmativa(s)
correta(s):
apenas II.a)
apenas I e III.b)
I, II e III.c)
apenas I.d)
apenas I e II.e)
(UFF) Uma função real de variável real8. f é tal que
 
= π  
1
f
2
e f(x +1) = x f(x) para todo x ∈ R. O valor
de f(7/2) é:
pa)
7b) p
p
2c)
15 p
8
d)
7 p
15
e)

18
EM_V_MAT_004
(UNESP) Uma pessoa parte de carro de uma cidade10.
X com destino a uma cidade Y. Em cada instante t (em
horas), a distância que falta para percorrer até o destino
é dada, em dezenas de quilômetros, pela função D,
definida por:
D(t) = 4 2
t 7
1
t 1
+ 
−  +
Considerando o percurso da cidade X até a cidade Y, a
distância, em média, por hora, que o carro percorreu foi:
40kma)
60kmb)
80kmc)
100kmd)
120kme)
(UFF) Sejam11. f e g funções reais de uma variável real
dadas por






3x + 4 , se x ≥ 1 x2
+ 1 , se x > 3
f(x) e g(x)
5x + 2 , se x < 1 5x - 5 , se x ≤ 3
Pede-se:
g[f(2)]a)
fb) −1
[g(0)]
(UFJF) Responda aos itens I e II, observando os gráficos12.
das duas funções f e g de R em R, respectivamente, do
1.º e 2.º graus, representados abaixo.
y
x
f
g
Sobre a função h = f + g de R em R, definida porI.
h(x) = f(x) + g(x), é correto afirmar que:
possui ponto de máximo.a)
possui ponto de mínimo.b)
é uma função crescente.c)
é uma função decrescente.d)
é uma função constante.e)
Sobre a função h = fog de R em R, definida por h(x)II.
= f(g(x)), é correto afirmar que:
possui ponto de máximo.a)
possui ponto de mínimo.b)
é uma função crescente. c)
é uma função decrescente.d)
é uma função constante.e)
(UFF) Considere as funções reais13. f, g e h definidas
por f(x) = log2
x 2
, g(x) = log2
x e h(x) = log 2/3
x.
Determine o valor de h (g (f(4))).
(UFCE) Considere a função f(x) =14.
cx
dx + 3
definida para
todo número real x tal que dx + 3 0, onde c e d são
constantes reais. Sabendo que f(f(x)) = x e f(5)
(3) =
f(f(f(f(f(3))))) = –3/5, podemos afirmar que c2
+d2
é
igual a:
(UFF) Na figura, o ponto R representa a localização,9.
à beira-mar, de uma usina que capta e trata o esgoto
de certa região. Com o objetivo de lançar o esgoto
tratado no ponto T, uma tubulação RQT deverá ser
construída.
800 m
2 km
Q R
cais
T
P
x
O ponto T situa-se a 800m do cais, em frente ao
ponto P, que dista 2km de R, conforme ilustração
acima.
O custo da tubulação usada no trajeto retilíneo
RQ, subterrâneo ao longo do cais, é de 100 reais
por quilômetro, e o custo da tubulação usada na
continuação QT, também retilínea, porém submarina,
é de 180 reais por quilômetro.
Sendo x a medida de PQ, a função f que expressa
o custo, em real, da tubulação RQT em termos de x,
em quilômetro, é dada por:
f(x) = 2 – x +a) 800 + x
f(x) = 200 – 100x + 180b) 0,64 + x2
f(x) =c) 0,64 + x2
+ x2
+ x
f(x) = 200 +d) 0,64 + x2
f(x) = 200 – 100x + 0,8xe) 2

19
EM_V_MAT_004
5a)
25b)
61c)
113d)
181e)
(UFF) Considere a função f definida por15.

4x , | x | < 4
f(x) = Pede-se:

x3
, | x | ≥ 4
f(0);a)
(fof) (–2);b)
o valor de m tal que f(m) = –125;c)
fd) –1
(1/4).
(UFMG) Nesta figura, está representado o gráfico da16.
função y = f(x), cujo domínio é o conjunto {x ∈ R: –6 ≤ x
≤ 6} e cuja imagem é o conjunto {y ∈ R: -2 ≤ y ≤ 3}:
y
x
1
3
2
4
6
0
-2
-3
-6
Sendo g(x) = f(x) +2 e h(x) = f(x +2),
1. Determine g(0) e h(0).
2. Esboce o gráfico de:
y = g(x)a)
y = h(x)b)
3. Determine os domínios das funções g e h.
(UFRN) Uma calculadora apresentava, em sua tela, o17.
resultado da soma dos gastos do mês realizados por
um pai “coruja” que permitiu a seu filho apertar algu-
mas teclas, alterando esse resultado. O pai observou
que o menino havia apertado as teclas , + ,
1 e , nessa ordem e uma única vez.
Para recuperar o resultado que estava na tela, o pai
deverá apertar as teclas
x2
a) , 1 , - e x2
.
x2
b) , - , 1 e x2
.
x2
c) , + , 1 e x2
.
x2
d) , 1 , + e x2
.
(UNIRIO) Sob pressão constante, conclui-se que18.
o volume V, em litros, de um gás e a temperatura T,
em graus Celsius, estão relacionados por meio da
equação:
V = Vo
+
Vo
273
T ,
onde Vo
denota o volume do gás a 0ºC. Assim, a
expressão que define a temperatura como função
do volume V é:
Vo
273
T = V – Voa)
V – Vo
273 Vo
T =b)
273V – Vo
Vo
T =c)
V – 273Vo
Vo
T =d)
V – Vo
Vo
T = 273e)
(ITA) Sejam f, g: R19. R definidas por f(x) = x3
e g(x) =
103⋅cos 5x
. Podemos afirmar que
f é injetora e par e g é ímpar.a)
g é sobrejetora e gof é par.b)
f é bijetora e gof é ímpar.c)
g é par e gof é ímpar.d)
f é ímpar e gof é par.e)
(UFF) Considere as retas20. r, s e t cujas equações são,
respectivamente, x/p + y = 1, x – py = p e 2x + 3y = 6,
com p ≠ 0.
Determine:
o valor dea) p para o qual r, s e t interceptam-se em
um único ponto M;
as coordenadas do ponto de interseção M.b)
(UFF) Com relação ao triângulo ABC sabe-se que:21.
o ponto A pertence ao eixo das abscissas;••
o ponto B pertence ao eixo das ordenadas;••

20
EM_V_MAT_004
a equação da reta que contém os pontos A e C é x +••
y + 5 = 0;
a equação da reta que contém os pontos B e C é 2x –••
y – 2 = 0.
Determine as coordenadas dos pontos A, B e C.
(UFF) Um motorista de táxi cobra, em cada corrida, o va-22.
lor fixo de R$3,20 mais R$0,80 por quilômetro rodado.
Indicando pora) x o número de quilômetros rodados
e por P o preço a pagar pela corrida, escreva a ex-
pressão que relaciona P com x.
Determine o número máximo de quilômetros roda-b)
dos para que, em uma corrida, o preço a ser pago
não ultrapasse R$120,00.
(UFF)Umrestaurantecobra,noalmoço,atéas16h,opreço23.
fixo de R$15,00 por pessoa. Após as 16 h, esse valor cai
paraR$12,00.Emdeterminadodia,50pessoasalmoçaram
no restaurante, sendo x o número de pessoas que almo-
çaram até as 16h. Sabendo que o custo de um almoço
é R$ 8,00 por pessoas e o lucro obtido pelo restaurante
naquelediafoimaiorqueR$250,00emenorqueR$300,00,
determine o menor e maior valor possível de x.
(UFF) Um reservatório, contendo inicialmente 400 litros24.
de água, começa a receber água a uma razão constante
de três litros por segundo, ao mesmo tempo que uma
torneira deixa escoar água desse reservatório a uma
razão, também constante, de um litro por segundo.
Considerando o instante inicial (t = 0) como o instante
em que o reservatório começou a receber água, de-
termine:
o volume de água no reservatório decorridos deza)
segundos (t = 10) a partir do instante inicial;
uma expressão para o volume (V), em litro, de águab)
no reservatório em função do tempo decorrido (t),
em segundo, a partir do instante inicial.
(UFRJ) Um videoclube propõe a seus clientes três25.
opções de pagamento:
Opção I: R$40,00 de taxa de adesão anual, maisa)
R$1,20 por DVD alugado.
Opção II: R$20,00 de taxa de adesão anual, maisb)
R$2,00 por DVD alugado.
Opção III: R$3,00 por DVD alugado, sem taxa dec)
adesão.
Um cliente escolheu a opção II e gastou R$56,00 no ano.
Esse cliente escolheu a melhor opção de pagamento
para o seu caso? Justifique a sua resposta.
(UFRJ) Maria faz hoje 44 anos e tem dado um duro26.
danado para sustentar suas três filhas: Marina, de 10
anos; Marisa, de 8 anos; e Mara, de 2 anos. Maria
decidiu que fará uma viagem ao Nordeste para visitar
seus pais, no dia do seu aniversário, quando sua idade
for igual à soma das idades de suas três filhas. Com que
idade Maria pretende fazer a viagem?
(UFF) A reta r contém o ponto P( −5, 0), tem coeficiente27.
angular negativo e forma, com os eixos coordenados,
um triângulo de área igual a 20. Determine a equação
de r.
(UFF) Um grande poluente produzido pela queima28.
de combustíveis fósseis é o SO2
(dióxido de enxofre).
Uma pesquisa realizada na Noruega e publicada na
revista “Science” em 1972 concluiu que o número (N)
de mortes por semana, causadas pela inalação de
SO2
, estava relacionado com a concentração média
(C), em mg/m3
, do SO2
conforme o gráfico abaixo: os
pontos (C, N) dessa relação estão sobre o segmento
de reta da figura.
C0 100 700
97
115
N
Combasenosdadosapresentados,arelaçãoentreNe
C (100 ≤ C ≤ 700) pode ser dada por:
N = 100 – 700Ca)
N = 94 + 0,03Cb)
N = 97 + 0,03Cc)
N = 115 – 94Cd)
N = 97 + 600Ce)

21
EM_V_MAT_004
B1.
A2.
C3.
C4.
x5. ∈ [0, 1] ∪ [3, 5]
–2, 0 e 5/26.
C7.
8.
f(-1) = 0 ea) f(0) = 1
2b)
Df = {x9. ∈ R x ≥ 3}
V, F, V, F, V10.
Dom f = (– 2, 1)11. ∪ (1, + ∞)
E12.
A13.
14.
0 ea) 3
3
8b)
15.
h(x) = –6x – 5a)
1 1x 1 x 2
f (x) e g (x)
3 2
− −− − −
= =b)
16.
1a)
–1b)
1c)
1d)
17.
2
2(x 1)
f(x)
x 2x 3
−
=
− −
a)
D(f) = {xb) ∈ R  x < −1 ou x > 3}

22
EM_V_MAT_004
C18.
19.
xa)
1 x 1
f (x)
x 1
− +
=
−
b)
20.
Df = { xa) ∈ R  x ≥ 1/2}
gb) –1
(x) = 1 –10x
B21.
Im (fogoh) = [ -3; +22. ∞ [
23.
(fog) (x) = xa) 2
S {x | x k , k Z}
2
π
= = + π ∈b)
A24.
B25.
C26.
D27.
28.
840a)
100 horas.b)
29.
18a)
5b)
12,5m.30.
24,26 bilhões de dólares.31.
D32.
B33.
R$34,00.34.
D35.
B36.
C37.
B38.
0,21.
Df = {x2. ∈ R  –1 < x < 1}
D3.
4.
D(f) = R* e Im(f) = R −{3}a)
Gráfico.b)
y
x
0 2
–1
5.
D(f) = {xa) ∈ R  −1 ≤ x < 0 ou 0 < x ≤ 1}
Demonstração.b)
Basta racionalizar a expressão de f.
2 2
2 2
( 1 x + 1 x ) 1 1 x
f(x)
x( 1 x ) ( 1 x )
+ − + −
= =
+ + −
6.
x, 1 x 0
0, 0 x 1
g(x)
2x 2, 1 x 2
2, 2 x 4
− − ≤ <
 ≤ <
= 
− ≤ <
 ≤ ≤
a)
b) [0,2]
c)
1, 0 x 2
f(x)
x 1, 2 x 4
≤ <

− ≤ ≤
B7.
D8.
B9.
C10.
11.
101a)
–7/5b)
12.
bI)
aII)
–113.
B14.

23
EM_V_MAT_004
15.
0a)
–512b)
–5c)
1/16d)
(1.) g(0) = 2 e h(0) = −216.
(2.)
a)
x
g(x)
2 6-3
3
-6
5
b)
-8
-5
-2
X
h (x)
1
3
4
(3.)
D(g) = {x R: −6 ≤ x ≤6} e D(h) = {x R: −8 ≤ x ≤ 4}
B17.
E18.
E19.
20.
p = 3a)
(3, 0)b)
21.
A (–5, 0)
B (0, –2)
C (–1, –4)
22.
P = 3,20 +0,80xa)
146km.b)
O menor valor possível para x é 17 e o maior valor pos-23.
sível para x é 33.
24.
420 litros.a)
V(t) = 400 +2tb)
Não, a melhor opção seria a opção III.25.
56 anos.26.
y = (-8/5) x - 827.
B28.

24
EM_V_MAT_004

Guia de Matemática para Pré-Vestibular

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Destaque

Destaque (20)

Semelhante a Guia de Matemática para Pré-Vestibular

Semelhante a Guia de Matemática para Pré-Vestibular (20)

Mais de Everton Moraes

Mais de Everton Moraes (20)

Último

Último (20)

Guia de Matemática para Pré-Vestibular