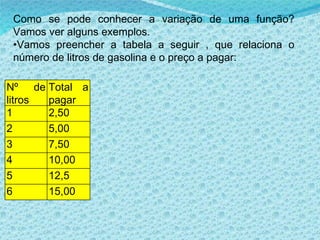
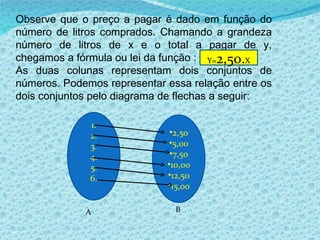
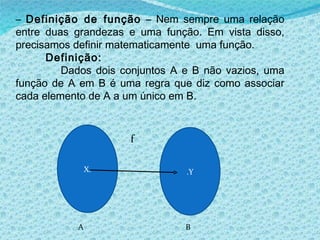
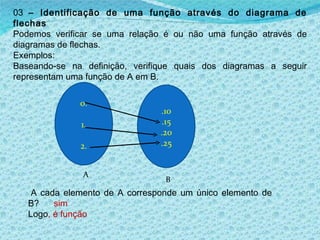
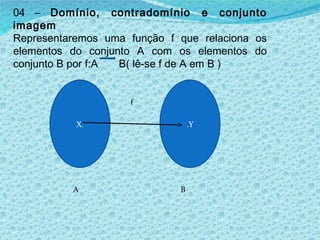
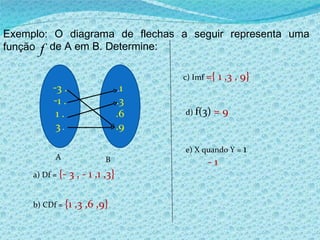
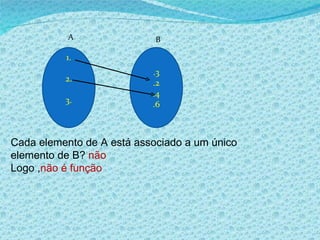
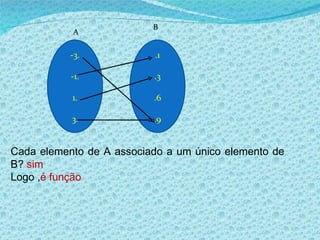
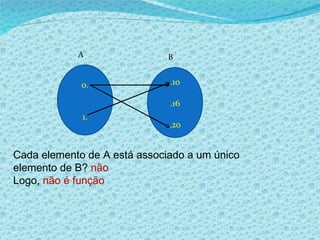
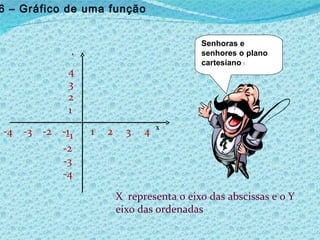
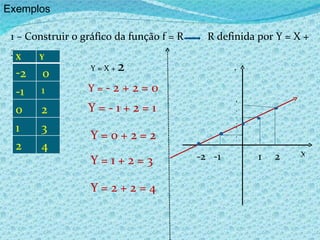
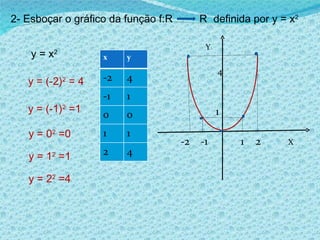
1) O documento discute noções básicas de funções matemáticas, incluindo exemplos de situações onde uma grandeza depende de outra e definições formais de domínio, contradomínio e conjunto imagem. 2) Apresenta exemplos de gráficos que representam funções e não funções. 3) Explica como construir e ler gráficos de funções.

1. FUNÇÕES 01 – Noções de funções – Função é um conceito muito importante na matemática e nas ciências. Para termos idéia do que é uma função, podemos pensar em duas grandezas que variam uma dependendo da outra. Observe as seguintes situações: A conta telefônica é função do número de ligações feitas. A conta de energia é função do consumo de energia dos aparelhos elétricos. O lucro do vendedor de sapatas está em função do número de pares vendidos por ele. A população de um país não é função, ou seja, não depende de sua área. O tempo que o avião leva para fazer uma viagem não é função do número de passageiros abordo.

2. Como se pode conhecer a variação de uma função? Vamos ver alguns exemplos. Vamos preencher a tabela a seguir , que relaciona o número de litros de gasolina e o preço a pagar: Nº de litros Total a pagar 1 2,50 2 5,00 3 7,50 4 10,00 5 12,5 6 15,00

3. Observe que o preço a pagar é dado em função do número de litros comprados. Chamando a grandeza número de litros de x e o total a pagar de y, chegamos a fórmula ou lei da função : As duas colunas representam dois conjuntos de números. Podemos representar essa relação entre os dois conjuntos pelo diagrama de flechas a seguir: 1. 2. 3. 4. 5. 6. 2,50 5,00 7,50 10,00 12,50 15,00 Y= 2,50. X A B

4. Em 1 segundo, quanto metro cai uma pedra? d=5.1 2 d=5.1 d=5 m Em 2 segundos, quantos metros caem uma pedra? d=5.2 2 d=5.4 d=20 m Em 3 segundos, quantos metros caem uma pedra ? d=5.3 2 d=5.9 d=45 m

5. – Definição de função – Nem sempre uma relação entre duas grandezas e uma função. Em vista disso, precisamos definir matematicamente uma função. Definição: Dados dois conjuntos A e B não vazios, uma função de A em B é uma regra que diz como associar cada elemento de A a um único em B. X. .Y A B f

6. 03 – Identificação de uma função através do diagrama de flechas Podemos verificar se uma relação é ou não uma função através de diagramas de flechas. Exemplos: Baseando-se na definição, verifique quais dos diagramas a seguir representam uma função de A em B. 0. 1. 2. .10 .15 .20 .25 A cada elemento de A corresponde um único elemento de B? sim Logo , é função A B

7. Cada elemento de A está associado a um único elemento de B? não Logo , não é função 1. 2. 3. .3 .2 .4 .6 A B

8. Cada elemento de A associado a um único elemento de B? sim Logo , é função -3. -1. 1. 3 . .1 .3 .6 .9 A B

9. Cada elemento de A está associado a um único elemento de B? não Logo, não é função 0. 1. .10 .16 .20 A B

10. 04 – Domínio, contradomínio e conjunto imagem Representaremos uma função f que relaciona os elementos do conjunto A com os elementos do conjunto B por f:A B( lê-se f de A em B ) X. .Y A B f

11. O conjunto A é chamado de Domínio e representaremos por D O conjunto B é chamado de contradomínio e representaremos porCD De forma genérica chamaremos os elementos do domínio de x. O elemento y é a imagem de x pela função Representaremos a imagem de x por f (x) Assim O subconjunto de B formado por todas as imagens de x é chamado conjunto imagem da função f e é indicado por Imf. .

12. Exemplo: O diagrama de flechas a seguir representa uma função de A em B. Determine: 3 . 1 . 1 . 3 . . 1 .3 .6 .9 a) Df = {- 3 , - 1 ,1 ,3} b) CDf = {1 ,3 ,6 ,9} c) Imf ={ 1 ,3 , 9} d) f(3) = 9 e) X quando Y = 1 - 1 A B

13. Dados os conjuntos A ={- 3 , -1 , 0 , 2} e conjunto B= {- 1 , 0 ,1 , 2 ,3 , 4} vamos considera a função f: A B , definida por f(x) = x + 2. 1)Determine: a) Df b) CDf c) Imf 2)Faça o diagrama 3. 1. 0. 2. .-1 .0 .1 .2 .3 .4 A B ={- 3 , -1 , 0 , 2} = {- 1 , 0 ,1 , 2 ,3 , 4 } f(x)=x+2 f(-3)=-3+2=-1 f(-1)=-1+2=1 f(0)=0+2=2 f(2)=2+2=4 Imf={-1,1,,2,4}

14. 06 – Gráfico de uma função Senhoras e senhores o plano cartesiano ! x y X representa o eixo das abscissas e o Y eixo das ordenadas -4 -3 -2 -1 1 2 3 4 4 3 2 1 -1 -2 -3 -4

15. Exemplos 1 – Construir o gráfico da função f = R R definida por Y = X + 2 Y = X + 2 Y = - 2 + 2 = 0 Y = - 1 + 2 = 1 Y = 0 + 2 = 2 Y = 1 + 2 = 3 Y = 2 + 2 = 4 -2 -1 1 2 4 3 2 1 X Y X Y 2 0 -1 1 0 2 1 3 2 4

16. 2- Esboçar o gráfico da função f:R R definida por y = x 2 y = x 2 y = (-2) 2 = 4 y = (-1) 2 =1 y = 0 2 =0 y = 1 2 =1 y = 2 2 =4 X Y 4 -2 -1 1 1 2 ‘ x y -2 4 -1 1 0 0 1 1 2 4