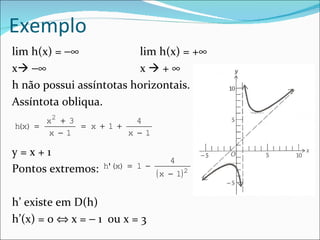
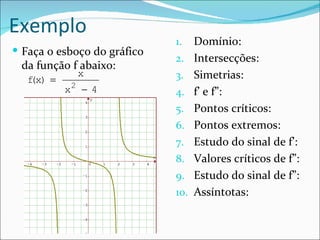
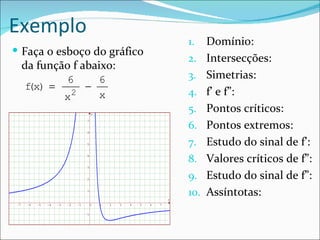
O documento aborda conceitos de cálculo como pontos críticos, extremos e concavidade de funções contínuas e deriváveis. Também define assíntotas verticais, horizontais e oblíquas, explicando como identificá-las e descrevendo procedimentos para esboçar gráficos de funções. Além disso, apresenta exemplos e exercícios para aplicar esses conceitos.

1. Profª Débora Bastos

2. Recapitulação
 P (c,f(c)) é crítico se f’(c) = 0 ou se f’(c) não existe.
 Para funções contínuas e deriváveis temos pontos
extremos nos pontos críticos.
 Para funções contínuas e deriváveis temos:
f crescente para valores de x em que f ’(x) > 0
f decrescente para valores de x em que f ’(x) < 0
f côncava para cima para valores de x em f ”(x) > 0
f côncava para baixo para valores de x em f ”(x) < 0
 Ponto de inflexão é o ponto em que há mudança de
concavidade. Ocorre entre os valores c tais que f ”(c)
não existe ou f ”(c) = 0.

3. Traçando um esboço do gráfico de uma
função
Temo até agora como determinar:
 Pontos extremos
 Intervalos onde a função é crescente ou decrescente
 Intervalos onde a função é côncava para cima ou para
baixo
 Pontos de Inflexão.
Falta ⇒ Estudo das assíntotas.

4. Exemplos
Assíntota
oblíqua
Assíntota
horizontal
Assíntota Assíntota
vertical vertical

5.  Definição 11: A reta x = a será uma assíntota vertical do
gráfico da função f, se pelo menos uma das afirmativas
abaixo for verdadeira:
(i) lim f(x) = + ∞
x  a+
(ii) lim f(x) = + ∞
x  a-
(iii) lim f(x) = − ∞
x  a+
(iv) lim f(x) = − ∞
x  a−

6.  Definição 12: A reta y = b é denominada uma assíntota 1
horizontal do gráfico da função f se pelo menos uma das
seguintes afirmações for válida:
(i) lim f(x) = b e para um nº N, se x > N, então f(x) ≠ b.
x  +∞
(ii) lim f(x) = b e para um nº N, se x < N, então f(x) ≠ b.
x  −∞

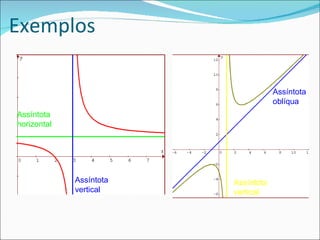
7.  Definição 13: Se lim [f(x) – (mx + b)] = 0
x ∞
então a reta y = mx + b é chamada assíntota oblíqua, pois a
distância vertical entre a curva y = mx + b e y = f(x) tende
a zero.
Nota: Se f(x) for uma função racional as assíntotas obliquas
ocorrem quando a diferença entre o grau do numerador e
do denominador é 1.

8. Exemplo
 Ache as assíntotas do gráfico da função h definida por:
x2 + 3
h x) =
(
x − 1
e faça um esboço do gráfico.
Solução:
D(h) = lR – {1}
Investigar o que ocorre à esquerda e à direita de x = 1.
lim h(x) = − ∞
x1-
lim h(x) = + ∞
x1+
A reta x = 1 é uma assíntota vertical de h.

9. Exemplo
lim h(x) = −∞ lim h(x) = +∞
x −∞ x+∞
h não possui assíntotas horizontais.
Assíntota obliqua.
x2 + 3 4
h x) =
( = x + 1 +
x − 1 x − 1
y=x+1
4
Pontos extremos: h'(x) = 1 −
( x − 1) 2
h’ existe em D(h)
h’(x) = 0 ⇔ x = − 1 ou x = 3

10. Procedimentos para obter o gráfico de uma
função bem detalhado.
h Determine o domínio de f;
n Ache a intersecção com o eixo oy se houver e se a
equação de f for fácil ache as raízes da função;
Teste a simetria em relação ao eixo oy (f(−x)=f(x)) e a
simetria em relação a origem (f(−x)= − f(x));
ç Calcule f ’(x) e f ”(x);
Determine os números críticos de f (f ’(x) não existe ou
f ’(x) = 0);
ú Verifique se os valores críticos são extremos (teste da
segunda derivada);
) Determine os intervalos em que f é crescente ou
decrescente (estudo do sinal de f ’);

11. 1. Obtenha os valores de x em que f ”(x) não existe
ou f ”(x)= 0;
2. Determine os intervalos em que o gráfico de f é côncavo
para cima ou para baixo (estudo do sinal de f ”).
Verifique se os valores críticos obtidos no passo
anterior são de inflexão;
3. Verifique a existência de possíveis assíntotas verticais,
horizontais e oblíquas.

12. Exemplo
1. Domínio:
 Faça o esboço do gráfico
2. Intersecções:
da função f abaixo:
f x) =
(
x 3. Simetrias:
x2 − 4 4. f’ e f”:
5. Pontos críticos:
6. Pontos extremos:
7. Estudo do sinal de f’:
8. Valores críticos de f”:
9. Estudo do sinal de f”:
10. Assíntotas:

13. Exemplo
1. Domínio:
 Faça o esboço do gráfico
2. Intersecções:
da função f abaixo:
6 6 3. Simetrias:
f x) =
( −
x 2 x 4. f’ e f”:
5. Pontos críticos:
6. Pontos extremos:
7. Estudo do sinal de f’:
8. Valores críticos de f”:
9. Estudo do sinal de f”:
10. Assíntotas:

14. Exercícios
 Faça o mesmo para:
3 2
f x) = (x − 1) x
(
x
f x) = e x
(