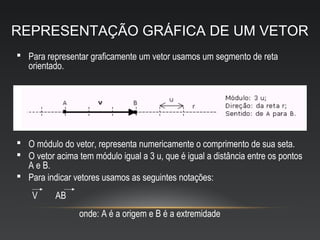
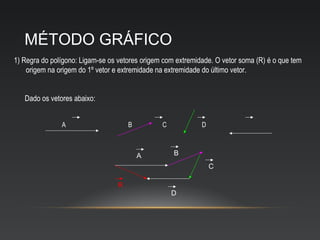
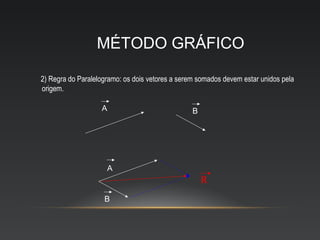
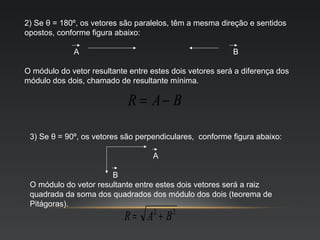
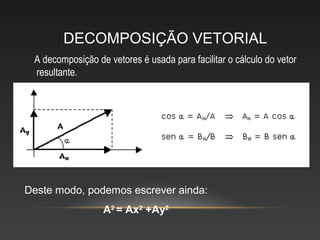
O documento descreve as propriedades de grandezas físicas escalares e vetoriais, incluindo a representação gráfica e operações com vetores, como adição, subtração, multiplicação e divisão. Grandezas escalares são expressas por valor e unidade, enquanto vetoriais requerem módulo, direção e sentido.

1. FÍSICA
PROFESSORA : ADRIANNE MENDONÇA

2. GRANDEZAS FÍSICAS
Podemos dizer de modo mais usual que grandeza é tudo aquilo que pode variar quantitativamente.
Deste modo, grandezas físicas são as que podem ser medidas.
São divididas em dois grupos: escalares e vetoriais.

3. GRANDEZAS ESCALARES E VETORIAIS
Grandezas escalares: ficam totalmente expressas por um valor e uma unidade.
Exemplos: temperatura, massa, calor, tempo, etc.
Grandezas vetoriais: são aquelas que não ficam totalmente determinadas com um valor e uma unidade, para que fiquem
totalmente definidas necessitam de módulo (número com unidade de medida), direção e sentido.
Exemplos: velocidade, força, aceleração, etc.

4. VETORES
Ente matemático abstrato, definido por um valor real (módulo
ou intensidade) associado a uma direção e um sentido.

5. REPRESENTAÇÃO GRÁFICA DE UM VETOR
 Para representar graficamente um vetor usamos um segmento de reta
orientado.
 O módulo do vetor, representa numericamente o comprimento de sua seta.
 O vetor acima tem módulo igual a 3 u, que é igual a distância entre os pontos
A e B.
 Para indicar vetores usamos as seguintes notações:
V AB
onde: A é a origem e B é a extremidade

6. PRINCIPAIS CARACTERÍSTICAS DE UM VETOR
• Módulo: comprimento do segmento (através de uma
escala pré-estabelecida).
O módulo de um vetor é indicado utilizando-se duas barras verticais.
|A| (Lê-se: módulo de A)
• Direção: reta que contém o segmento
• Sentido: orientação do segmento

7. VETOR OPOSTO
O vetor oposto é aquele que possui o mesmo módulo, a mesma
direção e o sentido oposto. Veja a seguir um exemplo com o vetor
e o seu respectivo oposto.
A -A

8. ADIÇÃO VETORIAL
• Determinação do vetor soma, ou vetor resultante a partir de dois ou
mais vetores.
• Pode ser efetuada através do método gráfico e do método analítico.

9. MÉTODO GRÁFICO
1) Regra do polígono: Ligam-se os vetores origem com extremidade. O vetor soma (R) é o que tem
origem na origem do 1º vetor e extremidade na extremidade do último vetor.
Dado os vetores abaixo:
A B C D
A B
C
R
D

10. MÉTODO GRÁFICO
2) Regra do Paralelogramo: os dois vetores a serem somados devem estar unidos pela
origem.
A B
A
R
B

11. MÉTODO ANALÍTICO
Podemos encontrar o módulo da resultante de dois vetores, sabendo-se apenas
o módulo dos vetores e o ângulo entre eles.
Exemplos: Sejam dois vetores de módulos A e B, e que formam entre si um
ângulo θ.
1) Se θ = 0º, os vetores são paralelos, têm a mesma direção e mesmo
sentido, conforme figura abaixo:
R = A+ B
A B
O módulo do vetor resultante entre estes dois vetores será a soma dos
módulo dos dois, chamado de resultante máxima.
R = A+ B

12. 2) Se θ = 180º, os vetores são paralelos, têm a mesma direção e sentidos
opostos, conforme figura abaixo:
A B
O módulo do vetor resultante entre estes dois vetores será a diferença dos
módulo dos dois, chamado de resultante mínima.
R = A− B
3) Se θ = 90º, os vetores são perpendiculares, conforme figura abaixo:
A
B
O módulo do vetor resultante entre estes dois vetores será a raiz
quadrada da soma dos quadrados dos módulo dos dois (teorema de
Pitágoras).
R= A + B2 2

13. 4) Se θ, for um ângulo qualquer, diferente dos mencionados anteriormente,
os vetores são oblíquos, conforme figura abaixo:
θ
A B
O módulo do vetor resultante entre estes dois vetores será dada pela lei dos
cosenos:
R = A2 + B 2 + 2 ⋅ A ⋅ B ⋅ cos α

14. DECOMPOSIÇÃO VETORIAL
A decomposição de vetores é usada para facilitar o cálculo do vetor
resultante.
Deste modo, podemos escrever ainda:
A2 = Ax2 +Ay2

15. MULTIPLICAÇÃO DE UM VETOR POR
UM NÚMERO REAL
Ao multiplicarmos um vetor qualquer (A) por um número real (n) positivo ou negativo,
inteiro ou fracionário, obtemos como resultado um vetor produto (P), com as
seguintes condições:
 O módulo do vetor P é igual a n x |A|.
 A direção é a mesma de A.
 O sentido é igual ao de A se n for positivo ou sentido oposto ao de
A se n for negativo.

16. DIVISÃO DE UM VETOR POR UM
NÚMERO REAL
Ao dividirmos um vetor qualquer (A) por um número real (n) obtemos como resultado
um vetor quociente (Q), com as seguintes condições:
 O módulo do vetor Q é igual a |A|/n.
 A direção é a mesma de A.
 O sentido é igual ao de A se n for positivo ou sentido oposto ao de
A se n for negativo.

17. http://br.geocities.com/saladefisica3/laboratorio/vetores/vetores.htm
http://br.geocities.com/saladefisica3/laboratorio/vetores2/vetores2.ht