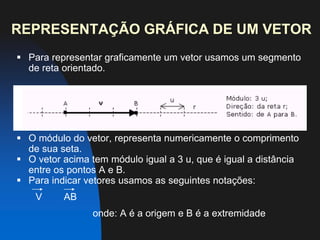
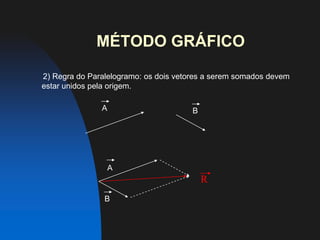
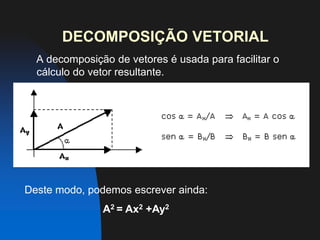
Vetores são entes matemáticos definidos por um valor real (módulo), direção e sentido. Eles podem ser representados graficamente por segmentos de reta orientados e somados através de métodos gráficos ou analíticos. Vetores podem também ser multiplicados ou divididos por números reais, alterando seu módulo mas mantendo direção e sentido.

1. VETORESProf. João Batista

2. GRANDEZAS FÍSICASPodemos dizer de modo mais usual que grandeza é tudo aquilo que pode variar quantitativamente.Deste modo, grandezas físicas são as que podem ser medidas.São divididas em dois grupos: escalares e vetoriais.

3. GRANDEZAS ESCALARES E VETORIAISGrandezas escalares: ficam totalmente expressas por um valor e uma unidade.Exemplos: temperatura, massa, calor, tempo, etc.Grandezas vetoriais: são aquelas que não ficam totalmente determinadas com um valor e uma unidade, para que fiquem totalmente definidas necessitam de módulo (número com unidade de medida), direção e sentido.Exemplos: velocidade, força, aceleração, etc.

4. VETORESEnte matemático abstrato, definido por um valor real (módulo ou intensidade) associado a uma direção e um sentido.

5. REPRESENTAÇÃO GRÁFICA DE UM VETORPara representar graficamente um vetor usamos um segmento de reta orientado.

6. O módulo do vetor, representanumericamente o comprimento de sua seta.

7. O vetoracima tem móduloigual a 3 u, que é igual a distância entre ospontos A e B.

8. Para indicarvetoresusamos as seguintesnotações: V AB onde: A é a origem e B é a extremidade

9. PRINCIPAIS CARACTERÍSTICAS DE UM VETORMódulo: comprimento do segmento (através de uma escala pré-estabelecida).O módulo de um vetor é indicado utilizando-se duas barras verticais. |A| (Lê-se: módulo de A)Direção: reta que contém o segmentoSentido: orientação do segmento

10. VETOR OPOSTOO vetor oposto é aquele que possui o mesmo módulo, a mesma direção e o sentido oposto. Veja a seguir um exemplo com o vetor e o seu respectivo oposto. A -A

11. ADIÇÃO VETORIALDeterminação do vetor soma, ou vetor resultante a partir de dois ou mais vetores.Pode ser efetuada através do método gráfico e do método analítico.

12. MÉTODO GRÁFICO1) Regra do polígono: Ligam-se os vetores origem com extremidade. O vetor soma (R) é o que tem origem na origem do 1º vetor e extremidade na extremidade do último vetor. Dado os vetores abaixo: A B C DBACRD

13. MÉTODO GRÁFICO 2) Regra do Paralelogramo: os dois vetores a serem somados devem estar unidos pela origem. ABARB

14. MÉTODO ANALÍTICOPodemos encontrar o módulo da resultante de dois vetores, sabendo-se apenas o módulo dos vetores e o ângulo entre eles. Exemplos: Sejam dois vetores de módulos A e B, e que formam entre si um ângulo θ.Se θ = 0º, osvetoressãoparalelos, têm a mesmadireção e mesmosentido, conformefiguraabaixo: A B O módulo do vetorresultante entre estesdoisvetoresserá a soma dos módulo dos dois, chamado de resultantemáxima.

15. 2) Se θ = 180º, os vetores são paralelos, têm a mesma direção e sentidos opostos, conforme figura abaixo: A BO módulo do vetor resultante entre estes dois vetores será a diferença dos módulo dos dois, chamado de resultante mínima.3) Se θ = 90º, os vetores são perpendiculares, conforme figura abaixo: A BO módulo do vetor resultante entre estes dois vetores será a raiz quadrada da soma dos quadrados dos módulo dos dois (teorema de Pitágoras).

16. 4) Se θ, for um ângulo qualquer, diferente dos mencionados anteriormente, os vetores são oblíquos, conforme figura abaixo:θ A BO módulo do vetor resultante entre estes dois vetores será dada pela lei dos cosenos: