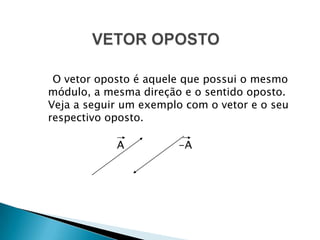
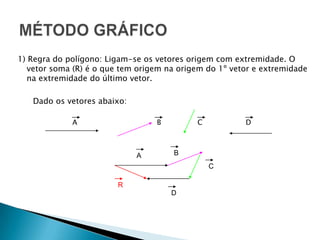
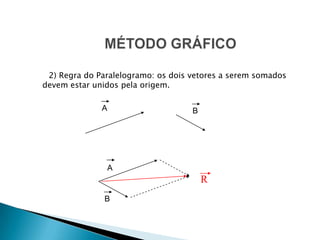
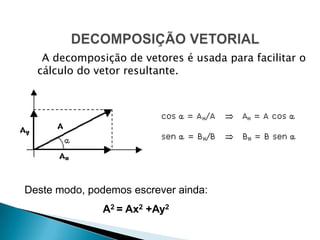
O documento discute vetores físicos, definindo-os como grandezas que necessitam de módulo, direção e sentido para serem totalmente determinadas, diferentemente de grandezas escalares. Apresenta a representação gráfica de vetores e métodos para a adição e decomposição vetorial, incluindo a multiplicação de um vetor por um número real.

1. VETORES

2. Podemos dizer de modo mais usual que grandeza é tudo aquilo que pode variar quantitativamente.Deste modo, grandezas físicas são as que podem ser medidas.São divididas em dois grupos: escalares e vetoriais.GRANDEZAS FÍSICAS

3. Grandezas escalares: ficam totalmente expressas por um valor e uma unidade.Exemplos: temperatura, massa, calor, tempo, etc.Grandezas vetoriais: são aquelas que não ficam totalmente determinadas com um valor e uma unidade, para que fiquem totalmente definidas necessitam de módulo (número com unidade de medida), direção e sentido.Exemplos: velocidade, força, aceleração, etc.GRANDEZAS ESCALARES E VETORIAIS

4. Ente matemático abstrato, definido por um valor real (módulo ou intensidade) associado a uma direção e um sentido.VETORES

5. REPRESENTAÇÃO GRÁFICA DE UM VETORPara representar graficamente um vetor usamos um segmento de reta orientado.

6. O módulo do vetor, representanumericamente o comprimento de sua seta.

7. O vetoracima tem móduloigual a 3 u, que é igual a distância entre ospontos A e B.

8. Para indicarvetoresusamos as seguintesnotações: V AB onde: A é a origem e B é a extremidade

9. PRINCIPAIS CARACTERÍSTICAS DE UM VETORMódulo: comprimento do segmento (através de uma escala pré-estabelecida).O módulo de um vetor é indicado utilizando-se duas barras verticais. |A| (Lê-se: módulo de A)Direção: reta que contém o segmentoSentido: orientação do segmento

10. VETOR OPOSTOO vetor oposto é aquele que possui o mesmo módulo, a mesma direção e o sentido oposto. Veja a seguir um exemplo com o vetor e o seu respectivo oposto. A -A

11. Determinação do vetor soma, ou vetor resultante a partir de dois ou mais vetores.Pode ser efetuada através do método gráfico e do método analítico.ADIÇÃO VETORIAL

12. 1) Regra do polígono: Ligam-se os vetores origem com extremidade. O vetor soma (R) é o que tem origem na origem do 1º vetor e extremidade na extremidade do último vetor. Dado os vetores abaixo:A B C DMÉTODO GRÁFICOBACRD

13. MÉTODO GRÁFICO 2) Regra do Paralelogramo: os dois vetores a serem somados devem estar unidos pela origem. ABARB

14. MÉTODO ANALÍTICOPodemosencontrar o módulodaresultante de doisvetores, sabendo-se apenas o módulo dos vetores e o ângulo entre eles. Exemplos: Sejam dois vetores de módulos A e B, e que formam entre si um ângulo θ.Se θ = 0º, osvetoressãoparalelos, têm a mesmadireção e mesmosentido, conformefiguraabaixo: A B O módulo do vetorresultante entre estesdoisvetoresserá a soma dos módulo dos dois, chamado de resultantemáxima.

15. 2) Se θ = 180º, os vetores são paralelos, têm a mesma direção e sentidos opostos, conforme figura abaixo: A BO módulo do vetor resultante entre estes dois vetores será a diferença dos módulo dos dois, chamado de resultante mínima.3) Se θ = 90º, os vetores são perpendiculares, conforme figura abaixo: A BO módulo do vetor resultante entre estes dois vetores será a raiz quadrada da soma dos quadrados dos módulo dos dois (teorema de Pitágoras).