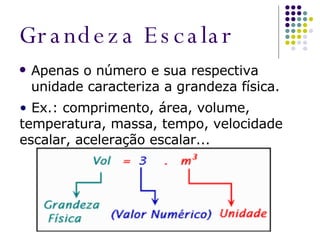
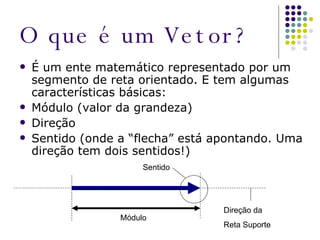
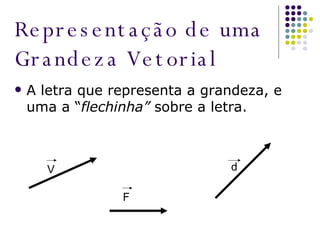
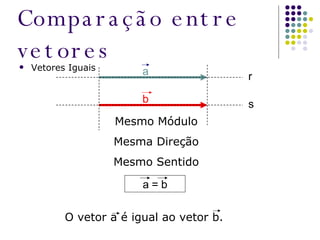
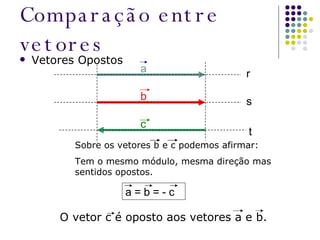
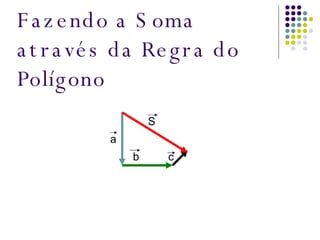
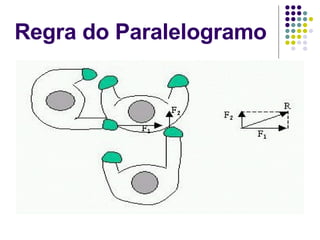
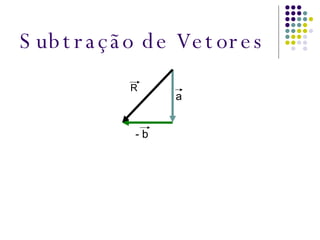
O documento aborda as diferenças entre grandezas escalares e vetoriais, explicando que grandezas vetoriais requerem mais que um número e unidade, como velocidade e força. Além disso, apresenta conceitos de soma e subtração de vetores, utilizando regras do polígono e do paralelogramo para encontrar o vetor resultante. O texto inclui exercícios para praticar a interpretação de grandezas físicas em situações específicas.

1. Vetores

2. Grandeza Escalar Apenas o número e sua respectiva unidade caracteriza a grandeza física. Ex.: comprimento, área, volume, temperatura, massa, tempo, velocidade escalar, aceleração escalar...

3. Grandeza Vetorial Algumas vezes necessitamos mais que um número e uma unidade para representar uma grandeza física. Sendo assim, surgiu uma representação matemática que expressa outras característica de uma grandeza: O VETOR Ex.: velocidade, aceleração, força, impulso, quantidade de movimento...

4. O que é um Vetor? É um ente matemático representado por um segmento de reta orientado. E tem algumas características básicas: Módulo (valor da grandeza) Direção Sentido (onde a “flecha” está apontando. Uma direção tem dois sentidos!) Módulo Sentido Direção da Reta Suporte

5. Representação de uma Grandeza Vetorial A letra que representa a grandeza, e uma a “ flechinha” sobre a letra. V F d

6. Comparação entre vetores Vetores Iguais Mesmo Módulo Mesma Direção Mesmo Sentido a b r s a = b O vetor a é igual ao vetor b.

7. Comparação entre vetores Vetores Opostos a b r s c t Sobre os vetores b e c podemos afirmar: Tem o mesmo módulo, mesma direção mas sentidos opostos. a = b = - c O vetor c é oposto aos vetores a e b.

8. Soma Vetorial Através da soma vetorial encontramos o vetor resultante. O vetor resultante seria como se todos os vetores envolvidos na soma fossem substituídos por um, e este tivesse o mesmo efeito. Existem duas regras para fazer a soma vetores.

9. Regra do Polígono É utilizada na adição de qualquer quantidade de vetores. Exemplo: Determinar a soma a + b + c Para isto devemos posicionar cada vetor junto ao outro de forma que a extremidade de um vetor coloca-se junto à origem do outro. E o vetor soma, ou vetor resultante, será o vetor que une a origem do primeiro do primeiro com a extremidade do último, formando assim um polígono. a b c

10. Fazendo a Soma através da Regra do Polígono a b c S

11. Regra do Paralelogramo É utilizada para realizar a adição de apenas dois vetores . Exemplo: A origem dos dois vetores deve estar no mesmo ponto. Traçar uma reta paralela a cada um deles, passando pela extremidade do outro. E o vetor soma, ou vetor resultante, será o vetor que une a origem dos dois vetores com o cruzamento das duas retas paralelas a cada vetor, formando assim um paralelogramo. a b Determinar a soma a + b.

12. Regra do Paralelogramo E o módulo, ou seja, o valor desse vetor resultante será dado por: R a b α R = a + b + 2.a.b.cos α 2 2 2 Reta Paralela ao vetor b e que passa pela extremidade do vetor a. Reta Paralela ao vetor a e que passa pela extremidade do vetor b.

13. Regra do Paralelogramo: Casos Particulares 1º ) α = 0º S = a + b 2º ) α = 180º S = a - b 3º ) α = 90º S = a + b 2 2 2

14. Regra do Paralelogramo

15. Subtração de vetores Considere os dois vetores a seguir: a b Realizar a subtração, a – b, é como somar a mais um vetor de mesma intensidade, mesma direção, mas de sentido oposto ao do vetor b originalmente representado. Na realidade, estaremos fazendo a adição do vetor a com um vetor oposto ao vetor b ( a + (-b) ).

16. Subtração de Vetores a - b R

17. Decomposição de vetores

18. Exercícios 1. A velocidade de um projétil é 20 m/s, horizontal e para a direita. Interprete as informações. Intensidade da velocidade: 20 m/s Direção: horizontal Sentido : direita Esses dados caracterizam a velocidade como grandeza vetorial.

19. 2. Assinale V (verdadeiro), ou F (falso), para as frases abaixo. ( ) Temperatura é grandeza escalar. ( ) Massa é grandeza escalar. ( ) Força é grandeza vetorial. ( ) A aceleração da gravidade é grandeza vetorial. ( ) Volume é grandeza escalar. ( ) Tempo é uma grandeza vetorial. V, V, V, V, V, F