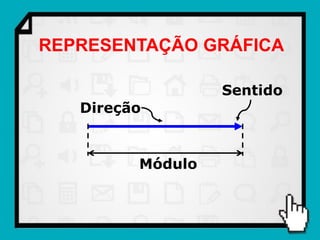
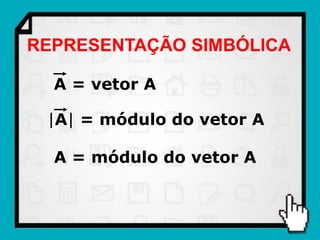
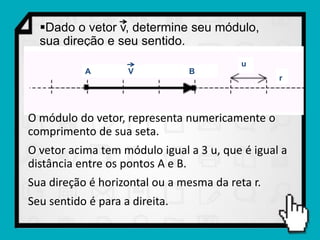
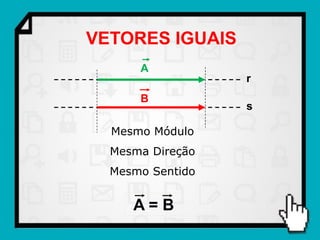
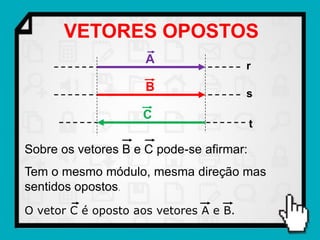
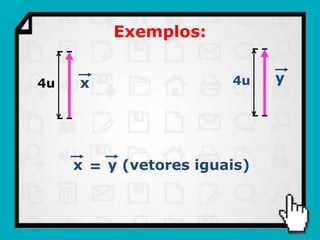
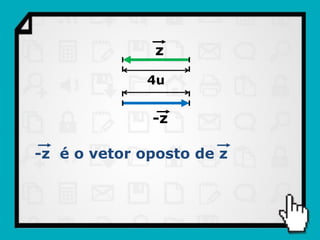
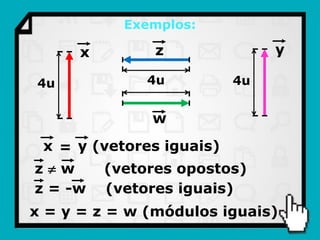
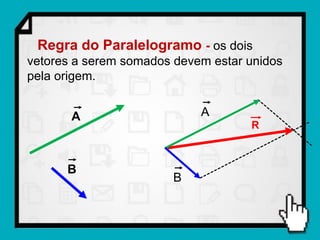
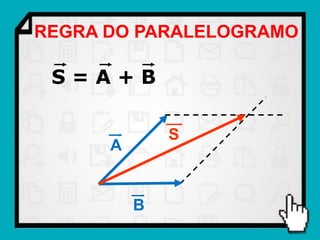
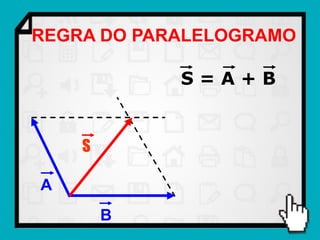
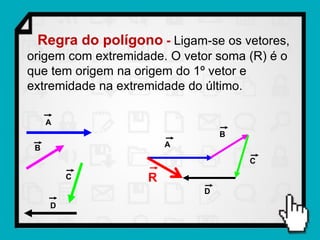
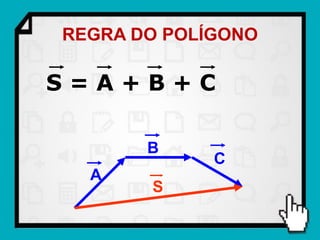
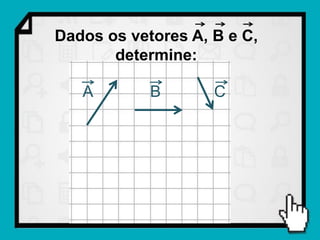
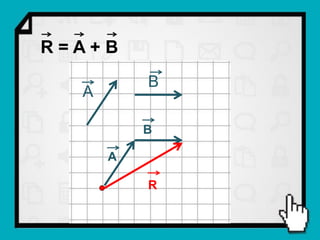
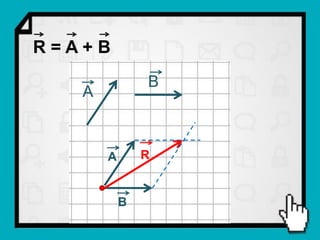
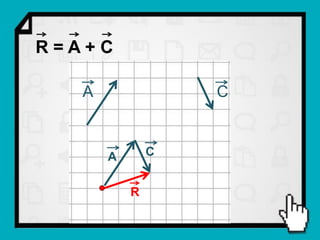
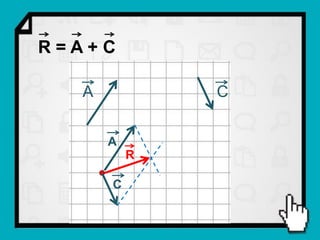
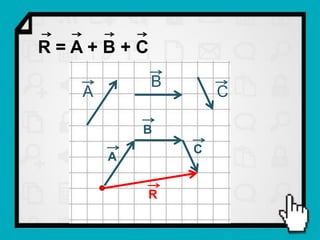
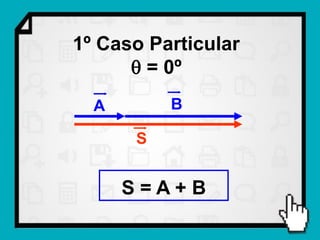
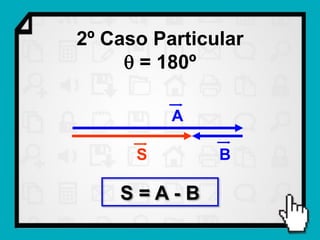
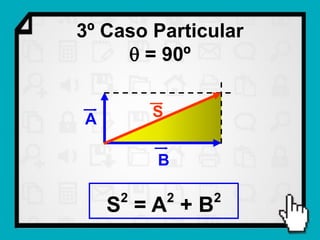
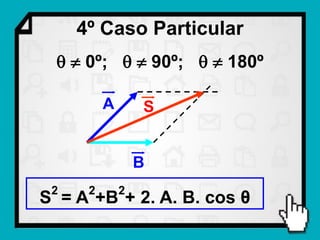
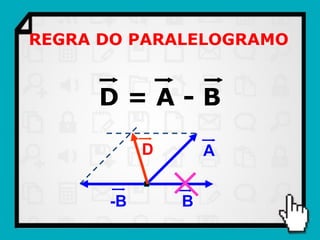
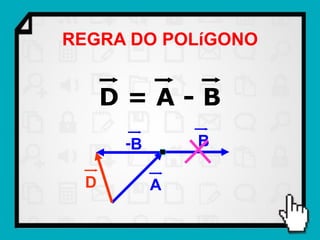
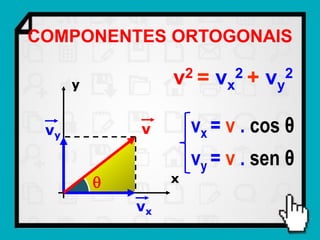
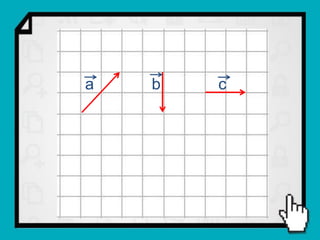
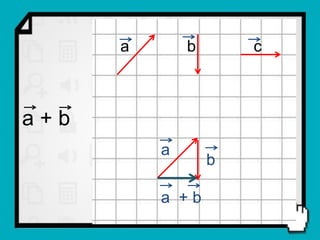
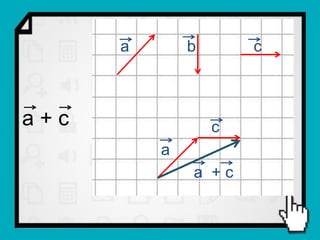
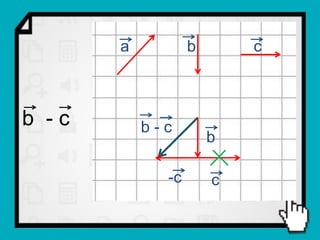
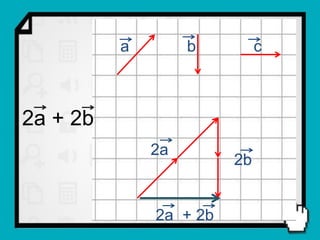
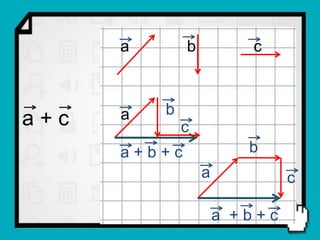
O documento discute conceitos fundamentais de vetores, incluindo: (1) grandezas escalares e vetoriais, (2) representação gráfica e simbólica de vetores, (3) propriedades como módulo, direção e sentido, (4) comparação entre vetores iguais e opostos, e (5) operações como soma e diferença utilizando as regras do paralelogramo e polígono.

1. FÍSICA
Prof. Amilcar

2. VETORES

3. GRANDEZAS
FÍSICAS

4. GRANDEZAS FÍSICAS
Grandeza Escalar Grandeza Vetorial
é toda grandeza é a grandeza física
física que está muito que para estar bem
bem definida apenas definida precisa de um
pelo seu módulo. complemento, ou seja
de uma orientação
(direção e sentido).

5. VETOR
É um ente matemático abstrato,
definido por um valor real (módulo ou
intensidade) associado a uma direção
e um sentido.

6. REPRESENTAÇÃO
Gráfica
Simbólica

7. REPRESENTAÇÃO GRÁFICA
Sentido
Direção
Módulo

8. REPRESENTAÇÃO SIMBÓLICA
A = vetor A
|A| = módulo do vetor A
A = módulo do vetor A

9. CARACTERÍSTICAS
Módulo: comprimento do segmento
(através de uma escala pré-estabelecida).
Direção: reta que contém o segmento
Sentido: orientação do segmento

10. Dado o vetor v, determine seu módulo,
sua direção e seu sentido.
u
A V B
r
O módulo do vetor, representa numericamente o
comprimento de sua seta.
O vetor acima tem módulo igual a 3 u, que é igual a
distância entre os pontos A e B.
Sua direção é horizontal ou a mesma da reta r.
Seu sentido é para a direita.

11. COMPARAÇÃO
Vetores Iguais
Vetores Opostos

12. VETORES IGUAIS
São vetores que possuem
mesmo módulo, mesma
direção e mesmo sentido.

13. VETORES IGUAIS
A
r
B
s
Mesmo Módulo
Mesma Direção
Mesmo Sentido
A=B

14. VETORES OPOSTOS
São vetores que possuem
mesmo módulo, mesma direção
e sentidos opostos.

15. VETORES OPOSTOS
A
r
B
s
C
t
Sobre os vetores B e C pode-se afirmar:
Tem o mesmo módulo, mesma direção mas
sentidos opostos.
O vetor C é oposto aos vetores A e B.

16. Exemplos:
4u x 4u y
x = y (vetores iguais)

17. z
4u
-z
-z é o vetor oposto de z

18. Exemplos:
x z y
4u 4u 4u
w
x = y (vetores iguais)
zw (vetores opostos)
z = -w (vetores iguais)
x = y = z = w (módulos iguais)

19. OPERAÇÕES COM VETORES
Soma
Diferença

20. SOMA VETORIAL
Através da soma vetorial
encontramos o vetor resultante.
O vetor resultante seria como se
todos os vetores envolvidos na
soma fossem substituídos por um,
e este tivesse o mesmo efeito.
Existem duas regras para fazer a
soma vetores.

21. SOMA
Método gráfico
Regra do Paralelogramo
Regra da Poligonal
Método algébrico

22. Regra do Paralelogramo - os dois
vetores a serem somados devem estar unidos
pela origem.
A A
R
B
B

23. REGRA DO PARALELOGRAMO
S=A+B
S
A
B

24. REGRA DO PARALELOGRAMO
S=A+B
S
A
B

25. Regra do polígono - Ligam-se os vetores,
origem com extremidade. O vetor soma (R) é o
que tem origem na origem do 1º vetor e
extremidade na extremidade do último.
A
B
B A
C
C R
D
D

26. REGRA DO POLÍGONO
S=A+B+C
B
C
A
S

27. EXERCÍCIO

28. Dados os vetores A, B e C,
determine:
A B C

29. R=A+B
B
A
B
A
R

30. R=A+B
B
A
A R
B

31. R=A+C
A C
A C
R

32. R=A+C
A C
A
R
C

33. R=A+B+C
B
A C
B
C
A
R

34. MÉTODO ALGÉBRICO

35. 1º Caso Particular
 = 0º
A B
S
S=A+B

36. 2º Caso Particular
 = 180º
A
S B
S=A-B

37. 3º Caso Particular
 = 90º
A S
B
2 2 2
S =A +B

38. 4º Caso Particular
  0º;   90º;   180º
A S
B
2 2 2
S = A +B + 2. A. B. cos θ

39. Observação
S=A+B
A- B≤ S ≤A + B

40. DIFERENÇA

41. REGRA DO PARALELOGRAMO
D=A-B
D A
-B B

42. REGRA DO POLíGONO
D=A-B
-B B
D A

43. COMPONENTES ORTOGONAIS
v2= vx2+ vy2
y
vy v vx = v . cos θ
vy = v . sen θ
 x
vx

44. EXERCÍCIO

45. a b c

46. a b c
a+b
a
b
a +b

47. a b c
a+c c
a
a +c

48. a b c
b -c b-c
b
-c c

49. a b c
2a + 2b
2a
2b
2a + 2b

50. a b c
a b
a+c c
a+b+c b
a c
a +b+c