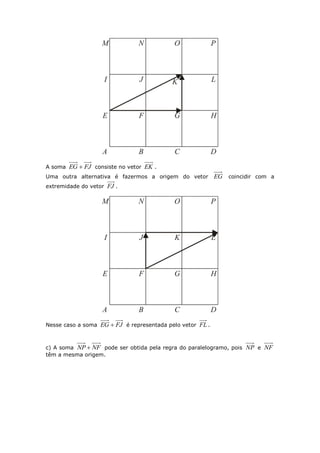
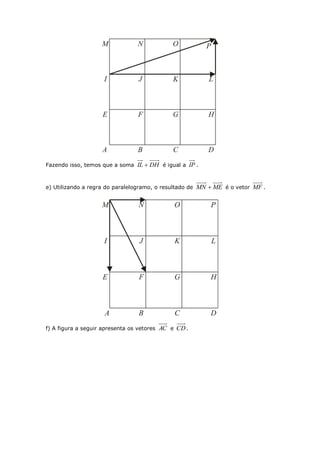
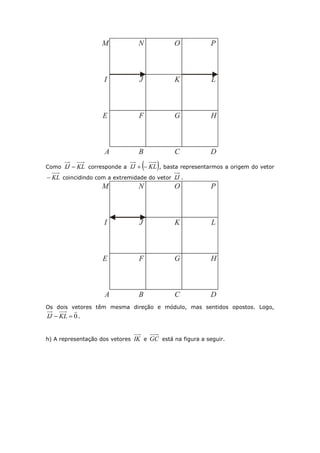
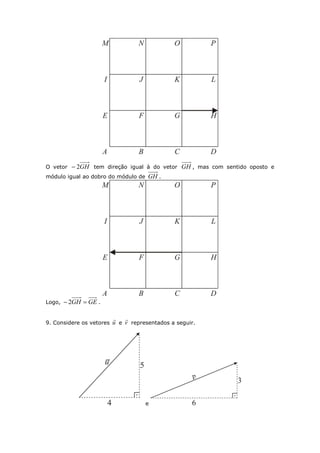
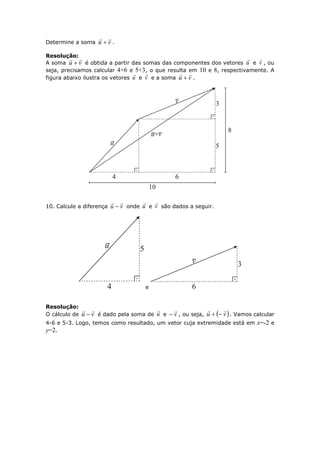
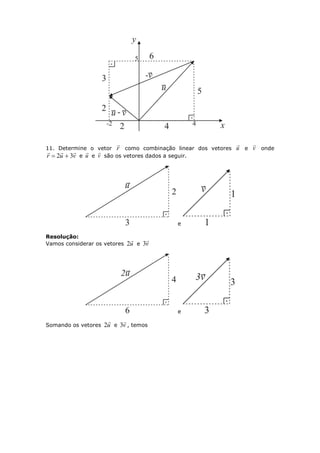
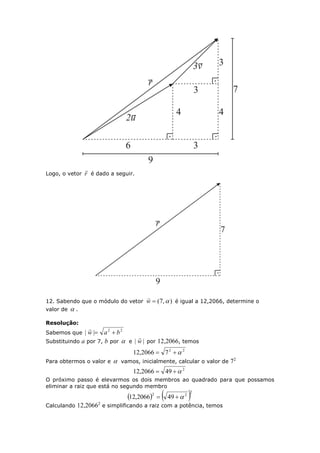
Este documento apresenta a resolução de diversos exercícios de Geometria Analítica com o objetivo de auxiliar os estudantes na aquisição e consolidação dos principais conceitos do assunto, como vetores, operações com vetores e suas propriedades. Antes de cada bloco de exercícios é fornecida uma breve explicação dos conteúdos necessários para a resolução.

1. Caderno de exercícios resolvidos e comentados
O presente caderno tem como objetivo apresentar de maneira clara e
objetiva a resolução de diversos exercícios de Geometria Analítica. Esse caderno é
mais do que simplesmente um conjunto de exercícios resolvidos. A nossa proposta
é auxiliar o estudante na aquisição e, principalmente, na consolidação dos
conhecimentos relacionados aos principais conteúdos da Geometria Analítica. O
intuito desses exercícios é proporcionar ao estudante a fixação dos procedimentos
necessários para a resolução dos problemas propostos e a fixação de operações
relativas aos temas abordados. Antes de cada conjunto de exercícios,
apresentaremos uma breve visão sobre os conteúdos que serão necessários para a
resolução dos exercícios propostos. Desde já desejamos bons estudos!
1. Vetores
1.1 Vetores
Vetor: um vetor é um segmento de reta que possui módulo, direção e sentido.
Módulo: o módulo é o comprimento do vetor e pode ser calculado pela fórmula
22
|| bav 

.
1.2 Casos particulares de vetores
Vetores paralelos: possuem a mesma direção.

2. Vetores iguais: possuem mesmo módulo, direção e sentido.
Vetor nulo: vetor de módulo igual a 0; qualquer ponto do espaço.

3. Vetores opostos: vetores de mesmo módulo e direção, mas de sentidos contrários.
Vetor unitário: vetor de módulo igual a 1.

4. Vetores ortogonais: vetores que formam um ângulo reto.
Vetores coplanares: vetores que estão no mesmo plano.
1.3 Inclinação de um vetor
A inclinação de um vetor é a medida  em relação à horizontal, no sentido anti-
horário.

5. ||
)(sen
v
b

||
)(cos
v
a

a
b
)(tg 
A tabela a seguir apresenta os valores do seno, cosseno e tangente para os arcos
notáveis correspondentes a 30°, 45° e 60° e será útil em muitos casos.
30° 45° 60°
sen
2
1
2
2
2
3
cos
2
3
2
2
2
1
tg
3
3
1 3
2. Operações envolvendo vetores
2.1 Produto de um vetor por um escalar
O produto de  por v

é o vetor v

 , onde 0

v , 0 , R .
2.2 Adição de vetores
ACvu 

ou ACBCAB 

6. ou
ACvu 

ou ACADAB 
2.3 Subtração de vetores
vuvu

 )(
DBvu 

ou DBCBDC 
Observação: As diagonais de um paralelogramo de lados iguais a u

e v

correspondem a vu

 e vu

 .

7. 2.4 Combinação linear de vetores
Um vetor v

é uma combinação linear dos vetores nvvv

,...,, 21 quando v

é a soma
dos múltiplos dos vetores nvvv

,...,, 21 :
nnvvvv

  2211 , onde Rn  ,...,, 21
Exercícios
1. Considere os pontos A, B, C e D localizados nos vértices do quadrado abaixo.
Dentre as afirmativas a seguir, determine quais são verdadeiras e quais são falsas.
a) CDAB //
b) ACAB //
c) BDAC //
d) CDAC 
e) BDAC 
f) BDCD 
Resolução:
a) Como AB e CD estão sobre os lados opostos do quadrado ABCD, AB e CD
são paralelos. Portanto a afirmação CDAB // é VERDADEIRA.

8. b) Os vetores AB e AC estão sobre dois lados adjacentes do quadrado ABCD.
Logo, AB e AC não são paralelos. Portanto a afirmação ACAB // é FALSA.
c) Os vetores AC e BD estão sobre dois lados paralelos do quadrado ABCD.
Logo, AC e BD são paralelos. Portanto a afirmação BDAC // é VERDADEIRA.

9. d) Observe que os vetores AC e CD estão sobre lados adjacentes do quadrado
ABCD. Logo AC e CD são ortogonais. Portanto, a afirmação CDAC  é
VERDADEIRA.
e) Como vimos no item (c), os vetores AC e BD estão sobre dois lados paralelos
do quadrado ABCD. Logo, AC e BD não são ortogonais. Portanto a afirmação
BDAC  é FALSA.
f) Os vetores CD e BD estão sobre lados adjacentes do quadrado ABCD. Logo
CD e BD são ortogonais. Portanto, a afirmação BDCD  é VERDADEIRA.

10. 2. Determine o módulo do vetor indicado na figura abaixo.
Resolução:
Sabemos que o módulo || v

consiste no comprimento do vetor v

. Para calcularmos
esse comprimento, podemos utilizar a fórmula
22
|| bav 

.
Como a=4 e b=3, vamos substituir esses valores na expressão
22
|| bav 

.
Fazendo essa substituição, temos
22
34|| v

O próximo passo é elevarmos 4 ao quadrado e também 3 ao quadrado que
resultam, respectivamente, em 16 e 9.
916|| v

Somando 16 e 9, temos 16+9=25
25|| v

Para, finalmente, encontrarmos o valor do módulo do vetor v

, precisamos calcular
a raiz quadrada de 25, o que é igual a 5
5|| v

Portanto, o módulo de v

, representado por || v

, é igual a 5.

11. 3. Determine a inclinação do vetor v

.
Resolução:
Para determinarmos a inclinação do vetor v

, podemos utilizar a relação
a
b
)(tg 
pois temos, nesse exercício, os valores de a e b. Sabemos que b é o cateto oposto
ao ângulo  e que a é o cateto adjacente a esse ângulo. Logo, b=3 e a=4.
Substituindo esses valores na fórmula
a
b
)(tg 
temos
4
3
)(tg 
Dividindo 3 por 4, o resultado é 0,75, ou seja,
75,0)(tg 
Precisamos agora determinar qual é o ângulo cuja tangente é igual a 0,75. Para
isso, vamos utilizar a função inversa
1
tg
, também conhecida como arco tangente e
representada por tgarc . O cálculo do arco tangente é feito facilmente com o uso de
uma calculadora científica. Para isso, o valor de  é dado por
75,0tgarc
Nesse caso, o valor de  é 36,87°. Portanto
 87,36
Obs.: O valor de  , com mais casas decimais, é 36,8698976...

12. Vamos usar a calculadora:
Para calcularmos o arco tangente, podemos utilizar uma calculadora científica.
Nesse caso, utilizaremos as teclas e .
Dependendo do modelo da calculadora, primeiro iremos fazer a divisão de b por a.
Depois deveremos pressionar a tecla [SHIFT] e em seguida a tecla [tan-1
]. Em
outros modelos, primeiro pressionamos a tecla [SHIFT], em seguida a tecla [tan-1
]
e depois digitamos, entre parênteses, a divisão de b por a.
Veja como é simples:
1° Caso: [3] [ ] [4] [=] [SHIFT] [tan-1
]
2° Caso: [SHIFT] [tan-1
] [(] [3] [ ] [4] [)] [=]
Obs.: Dependendo do modelo da calculadora, vamos encontrar a tecla [2ndf] no
lugar da tecla [SHIFT].
4. Determine o módulo e a inclinação do vetor v

.

13. Resolução:
Nesse exercício temos dois itens a serem calculados: o módulo e a inclinação do
vetor. Para calcularmos o módulo de v

, vamos utilizar a fórmula
22
|| bav 

.
É importante ressaltar que a=9 e b=5. Vamos agora substituir esses valores na
fórmula
22
|| bav 

.
Substituindo a por 9 e b por 5, temos
22
59|| v

Ao elevarmos 9 e 5 ao quadrado, temos, respectivamente, em 81 e 25. Logo
2581|| v

Efetuando a soma, temos 81+25 que é igual a 106
106|| v

O próximo passo é calcularmos a raiz quadrada de 106. Com o auxílio de uma
calculadora, o resultado é 10,3.
3,10|| v

Sendo assim, o módulo de v

é igual a 10,3. Note que temos as componentes do
vetor v

e também o módulo de v

. Por isso, para calcularmos a inclinação do vetor
v

, podemos usar uma das seguintes relações
||
)(sen
v
b

||
)(cos
v
a

a
b
)(tg 
Vamos utilizar a relação
a
b
)(tg  .
Inicialmente vamos considerar o ângulo  indicado na figura a seguir
Para que possamos calcular o valor de  , precisaremos calcular o valor de  .
Como  180 , temos que  180 . Para calcularmos  , basta utilizarmos
a relação
a
b
)(tg 
Substituindo a por 9 e b por 5 na fórmula, temos
9
5
)(tg 
Efetuando a divisão de 5 por 9, temos 0,56. Portanto

14. 56,0)(tg 
Vamos determinar qual é o ângulo  cuja tangente é igual a 0,56. Para isso, basta
calcularmos o arco tangente de 0,56
56,0tgarc
Com o uso de uma calculadora científica, chegamos à conclusão que  é igual a
29,25°. Portanto
 25,29
Vamos determinar agora o valor de  . Como  180 , e  25,29 , temos
 25,29180
Logo
 75,150
ou seja, a inclinação do vetor v

é igual a 150,75°.
5. Determine a inclinação do vetor u

.
Resolução:
Como o vetor u

está sobre uma reta horizontal e seu sentido é da esquerda para a
direita, a sua inclinação é igual a zero. Para comprovarmos isso, vamos fazer os
cálculos necessários. Sabemos que
a
b
)(tg 
e que, nessa situação, a=7 e que b=0.
Substituindo a e b por 7 e 0, respectivamente, temos
7
0
)(tg 
Dividindo 0 por 7, o resultado é igual a 0
0)(tg 
Para encontrarmos o valor de  , vamos calcular o arco tangente de 0
0tgarc
Finalmente, o arco tangente de 0 é igual a 0. Logo, 0 . Portanto, a inclinação do
vetor u

é igual a 0.
6. Qual é a inclinação do vetor v

?
Resolução:
A inclinação do vetor é igual a 180°. Observe que v

está sobre uma reta horizontal
e o sentido de v

é da direita para a esquerda.
7. O que é um vetor nulo?

15. Resolução:
Um vetor v

é dito nulo quando 0|| v

. Podemos representar um vetor nulo por um
único ponto.
8. O quadrado abaixo apresenta a posição dos pontos A a P.
Determine o vetor associado a cada uma das seguintes operações.
a) AEAB 
b) FJEG 
c) NFNP 
d) DHIL 
e) MEMN 
f) CDAC 
d) KLIJ 
h) GCIK 
i) MN3
j) GH2
Resolução:
a) Na figura abaixo temos a representação dos vetores AB e AE . Como ambos
têm a mesma origem, podemos utilizar a regra do paralelogramo para
encontrarmos a soma. Logo, AFAEAB  .

16. b) Os vetores EG e FJ estão representados na figura abaixo.
Para podermos encontrar a soma desses vetores, vamos coincidir a origem do vetor
FJ com a extremidade do vetor EG .

17. A soma FJEG  consiste no vetor EK .
Uma outra alternativa é fazermos a origem do vetor EG coincidir com a
extremidade do vetor FJ .
Nesse caso a soma FJEG  é representada pelo vetor FL .
c) A soma NFNP  pode ser obtida pela regra do paralelogramo, pois NP e NF
têm a mesma origem.

18. Nesse caso, o resultado da soma é o vetor NH .
d) A figura abaixo ilustra os vetores IL e DH .
Vamos representar o vetor DH de modo que a sua origem coincida com a
extremidade do vetor IL .

19. Fazendo isso, temos que a soma DHIL  é igual a IP .
e) Utilizando a regra do paralelogramo, o resultado de MEMN  é o vetor MF .
f) A figura a seguir apresenta os vetores AC e CD.

20. Para calcularmos CDAC  vamos determinar o oposto do vetor CD, o que
corresponde ao vetor CD , representado na figura abaixo.
A subtração CDAC  corresponde à soma  CDAC  , o que resulta no vetor
AB . Observe que a origem do vetor CD coincide com a extremidade do vetor
AC .
g) Inicialmente, vamos representar os vetores IJ e KL .

21. Como KLIJ  corresponde a  KLIJ  , basta representarmos a origem do vetor
KL coincidindo com a extremidade do vetor IJ .
Os dois vetores têm mesma direção e módulo, mas sentidos opostos. Logo,
0

 KLIJ .
h) A representação dos vetores IK e GC está na figura a seguir.

22. Fazendo  GCIKGCIK  , e representando o vetor GC de modo que sua
origem coincida com a extremidade de IK , temos que IOGCIK  .
i) O vetor MN está representado na figura a seguir.

23. A multiplicação do vetor MN pelo escalar 3 resulta em um vetor de mesma direção
e sentido do que MN , as com módulo 3 vezes maior do que o módulo de MN .
Portanto, MPMN 3 .
j) A representação do vetor GH pode ser vista na figura a seguir.

24. O vetor GH2 tem direção igual à do vetor GH , mas com sentido oposto e
módulo igual ao dobro do módulo de GH .
Logo, GEGH  2 .
9. Considere os vetores u

e v

representados a seguir.
e

25. Determine a soma vu

 .
Resolução:
A soma vu

 é obtida a partir das somas das componentes dos vetores u

e v

, ou
seja, precisamos calcular 4+6 e 5+3, o que resulta em 10 e 8, respectivamente. A
figura abaixo ilustra os vetores u

e v

e a soma vu

 .
10. Calcule a diferença vu

 onde u

e v

são dados a seguir.
e
Resolução:
O cálculo de vu

 é dado pela soma de u

e v

 , ou seja,  vu

 . Vamos calcular
4-6 e 5-3. Logo, temos como resultado, um vetor cuja extremidade está em x=-2 e
y=2.

26. 11. Determine o vetor r

como combinação linear dos vetores u

e v

onde
vur

32  e u

e v

são os vetores dados a seguir.
e
Resolução:
Vamos considerar os vetores u

2 e v

3
e
Somando os vetores u

2 e v

3 , temos

27. Logo, o vetor r

é dado a seguir.
12. Sabendo que o módulo do vetor ),7( w

é igual a 12,2066, determine o
valor de  .
Resolução:
Sabemos que
22
|| baw 

Substituindo a por 7, b por  e || w

por 12,2066, temos
22
72066,12 
Para obtermos o valor e  vamos, inicialmente, calcular o valor de 72
2
492066,12 
O próximo passo é elevarmos os dois membros ao quadrado para que possamos
eliminar a raiz que está no segundo membro
   2
22
492066,12 
Calculando 12,20662
e simplificando a raiz com a potência, temos

28. 2
490011,149 
Como 149,0011 é igual a 49+ 2
, podemos escrever, equivalentemente, que 49+ 2
é igual a 149,0011
0011,14949 2

Subtraindo 49 dos dois membros, temos
490011,1494949 2
 
que resulta em:
0011,1002

Vamos agora extrair a raiz quadrada dos dois membros
0011,1002

Isso nos leva a
000055,10
Logo,  = 10. Graficamente, o vetor w

é representado como segue
13. Determine as componentes do vetor v

sabendo que seu módulo é igual a 17 e
sua inclinação é igual a 60°.
Resolução:
Se conhecemos o módulo do vetor e a sua inclinação, podemos utilizar as relações
a seguir para encontrarmos as componentes a e b do vetor v

.
||
)(sen
v
b

||
)(cos
v
a

Sabemos que  60 e que 17|| v

. Inicialmente, vamos calcular o valor de b
||
)(sen
v
b

O primeiro passo é substituirmos os valores de  e de || v

por 60° e 17,
respectivamente

29. 17
)60(sen
b

Como
2
3
)60(sen  , podemos escrever
172
3 b

Multiplicando b por 2 e 3 por 17, temos
3172 b
Dividindo ambos os membros por 2, temos
2
317
b
Para obtermos o valor de b na forma decimal, basta calcularmos o valor da raiz
quadrada de 3, multiplicarmos esse resultado por 17 e, depois, dividirmos esse
valor por 2:
72,14b
O cálculo de a pode ser feito de forma análoga ao cálculo de b. Para isso, vamos
utilizar a relação
||
)(cos
v
a

Substituindo  por 60° e || v

por 17 temos
17
)60(cos
a

Vamos agora substituir )60(cos  por
2
1
172
1 a

Multiplicaremos a por 2 e 17 por 1
1x172 a
Donde
172 a
Dividindo ambos os membro por 2, temos
2
17
a
Finalmente, dividindo 17 por 2, temos o valor de a
5,8a
Sendo assim, as componentes do vetor v

são 5,8a e 72,14b . A representação
de v

é dada por

30. 14. Sejam )1,1(u

e )2,3(v

. Calcule o módulo de vu

45  .
Resolução:
Para calcularmos o módulo de vu

45  , primeiro precisamos obter as componentes
do vetor vu

45  .
)2,3(4)1,1(545  vu

Vamos agora multiplicar cada componente do vetor (1, 1) por 5 e cada componente
do vetor (3, 2) por 4
)8,12()5,5(45  vu

O próximo passo é somarmos as respectivas componentes, ou seja, 5+12 e 5+8
)31,17(45  vu

Agora que já sabemos quais são as componentes de vu

45  , vamos calcular o seu
módulo
22
1317|45|  vu

Elevando 17 e 13 ao quadrado, temos
169289|45|  vu

Vamos agora somar 289 com 169
458|45|  vu

Para obtermos o valor de |45| vu

 , vamos calcular a raiz quadrada de 458
4,21|45|  vu

Portanto, o módulo de |45| vu

 é igual a 21,4.