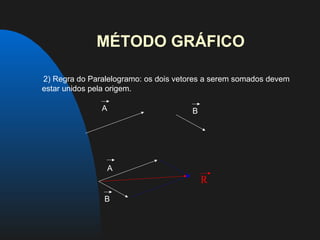
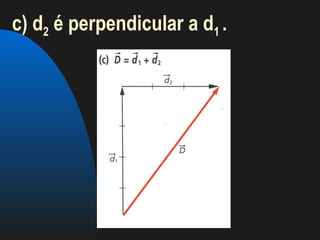
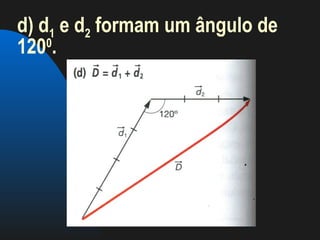
Este documento apresenta conceitos fundamentais sobre forças e vetores. Explica que força é toda ação capaz de produzir ou modificar um movimento. Apresenta grandezas físicas escalares e vetoriais, e detalha as características de vetores como módulo, direção e sentido. Demonstra métodos gráficos e analíticos para representar e somar vetores. Por fim, fornece exercícios sobre o tema.

1. Governo do Estado de Rondônia
Secretaria de Estado da Educação – SEDUC
E.E.E.F.M. Cel. Aluízio Pinheiro Ferreira
Rolim de Moura – RO
Estudo da Forças
Vetores
Prof.ª.: Daniela Fontana Almenara

2. Força
 É toda ação capaz de produzir ou modificar um
movimento ou deformar um corpo. Força é
resultado da interação entre corpos, em outras
palavras, um corpo só pode sofrer a ação de uma
força se ela for exercida por outro corpo.
 EX:
 Rebater uma bola lançada
 Puxar ou comprimir uma mola
 O salto de um paraquedista de um avião

3. GRANDEZAS FÍSICAS
Podemos dizer de modo mais usual que grandeza é tudo
aquilo que pode variar quantitativamente.
Deste modo, grandezas físicas são as que podem ser
medidas.
São divididas em dois grupos: escalares e vetoriais.

4. GRANDEZAS ESCALARES E VETORIAIS
Grandezas escalares: ficam totalmente expressas por um
valor e uma unidade.
Exemplos: temperatura, massa, calor, tempo, etc.
Grandezas vetoriais: são aquelas que não ficam totalmente
determinadas com um valor e uma unidade, para que
fiquem totalmente definidas necessitam de módulo (número
com unidade de medida), direção e sentido.
Exemplos: velocidade, força, aceleração, etc.

5. VETORES
Ente matemático abstrato, definido por um valor
real (módulo ou intensidade) associado a uma
direção e um sentido.

6. REPRESENTAÇÃO GRÁFICA DE UM VETOR
 Para representar graficamente um vetor usamos um segmento
de reta orientado.
 O módulo do vetor, representa numericamente o comprimento
de sua seta.
 O vetor acima tem módulo igual a 3 u, que é igual a distância
entre os pontos A e B.
 Para indicar vetores usamos as seguintes notações:
V AB
onde: A é a origem e B é a extremidade

7. PRINCIPAIS CARACTERÍSTICAS DE UM VETOR
 Módulo: comprimento do segmento
(através de uma escala pré-estabelecida).
O módulo de um vetor é indicado utilizando-se duas barras verticais.
|A| (Lê-se: módulo de A)
 Direção: reta que contém o segmento
 Sentido: orientação do segmento

8. VETOR OPOSTO
O vetor oposto é aquele que possui o mesmo módulo,
a mesma direção e o sentido oposto. Veja a seguir um
exemplo com o vetor e o seu respectivo oposto.
A -A

9. ADIÇÃO VETORIAL
 Determinação do vetor soma, ou vetor resultante a
partir de dois ou mais vetores.
 Pode ser efetuada através do método gráfico e do
método analítico.

10. MÉTODO GRÁFICO
1) Regra do polígono: Ligam-se os vetores origem com extremidade. O vetor soma
(R) é o que tem origem na origem do 1º vetor e extremidade na extremidade do
último vetor.
Dado os vetores abaixo:
A B C D
A B
C
R
D

11. MÉTODO GRÁFICO
2) Regra do Paralelogramo: os dois vetores a serem somados devem
estar unidos pela origem.
A B
A
R
B

12. MÉTODO ANALÍTICO
Podemos encontrar o módulo da resultante de dois vetores, sabendo-se apenas
o módulo dos vetores e o ângulo entre eles.
Exemplos: Sejam dois vetores de módulos A e B, e que formam entre si um
ângulo θ.
1) Se θ = 0º, os vetores são paralelos, têm a mesma direção e mesmo
sentido, conforme figura abaixo:
A B
O módulo do vetor resultante entre estes dois vetores será a soma dos
módulo dos dois, chamado de resultante máxima.
R = A+ B

13. 2) Se θ = 180º, os vetores são paralelos, têm a mesma direção e sentidos
opostos, conforme figura abaixo:
A B
O módulo do vetor resultante entre estes dois vetores será a diferença dos
módulo dos dois, chamado de resultante mínima.
R = A− B
3) Se θ = 90º, os vetores são perpendiculares, conforme figura abaixo:
A
B
O módulo do vetor resultante entre estes dois vetores será a raiz
quadrada da soma dos quadrados dos módulo dos dois (teorema de
Pitágoras).
R= A + B2 2

14. 4) Se θ, for um ângulo qualquer, diferente dos mencionados anteriormente,
os vetores são oblíquos, conforme figura abaixo:
θ
A B
O módulo do vetor resultante entre estes dois vetores será dada pela lei dos
cosenos:
R = A2 + B 2 + 2 ⋅ A ⋅ B ⋅ cos α

15. Resultante de vários vetores
 Consideremos dois deslocamentos, d1 e d2, de
módulos d1= 4 m d2= 3 m. Determine a resultante
D desses deslocamentos nos seguintes casos.

16. a) d1 e d2 têm a mesma direção e o
mesmo sentido.

17. b) d1 e d2 têm a mesma direção e
sentidos contrários.

18. c) d2 é perpendicular a d1 .

19. d) d1 e d2 formam um ângulo de
120 .
0

20. EXERCÍCIOS
 Lista de exercícios impressos. Clique aqui para
acessar
 Livro pág. 74 exercícios1, 3 e 4
 Livro pág. 79 exercícios 5, 6, 7, 10 e 11