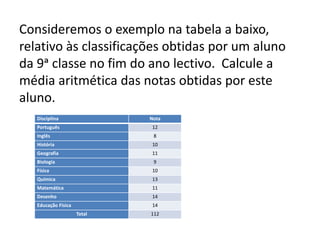
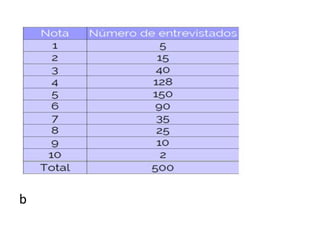
Este documento descreve medidas de tendência central como média, mediana e moda. Explica como calcular a média aritmética, média ponderada, e define moda e mediana. Fornece exemplos de como aplicar esses conceitos para caracterizar conjuntos de dados.

1. Medidas de tendência central:
média, moda e mediana
As medidas de tendência central são utilizadas
para caracterizar um conjunto de valores,
representando-o adequadamente.
A denominação “medida de tendência central”,
se deve ao facto de que, por ser uma medida que
caracteriza um conjunto, tenderá a estar no meio
dos valores. Além da média aritmética, iremos
tratar da mediana e a moda.

2. As medidas de tendência central são a média,
mediana e moda. Estas medidas são indicativas
de informação contida nos gráficos ou tabelas.
Para cada caso, dependendo do contexto do
problema em estudo, estas medidas devem ser
convenientemente utilizadas.
Alguns cálculos envolvendo média podem ser
efectuados por meio dos critérios de média
simples (aritmética) ou média ponderada.

3. Média aritmética (ou simplesmente média) de
um conjunto de dados numéricos é o número
que se obtém somando os valores de todos os
dados e dividir pelo número total de dados, e é
representado por

4. Consideremos o exemplo na tabela a baixo,
relativo às classificações obtidas por um aluno
da 9ᵃ classe no fim do ano lectivo. Calcule a
média aritmética das notas obtidas por este
aluno.
Disciplina Nota
Português 12
Inglês 8
História 10
Geografia 11
Biologia 9
Física 10
Química 13
Matemática 11
Desenho 14
Educação Física 14
Total 112

5. =
12+8+10+11+9+10+13+11+14+14
10
=
112
10
= 11,2
A média é um valor representativo. Ela serve
para resumir, em um número simples uma série
de valores sobre algo que está sendo observado.
No exemplo acima, quer parecer que em cada
disciplina o aluno teve 11,2 valores.

6. A média não representa bem o grupo, e o uso
desse resultado pode desencadear conclusões
falsas. Por exemplo, a média da quantidade de
filhos por mulher é 1,86. Ao fazer a análise, há
quem considere a possibilidade de alguém ter
1,86 filho. Calcular a média, nesse caso, não
faria sentido.
Esta média nesse caso indica que, ao repartir o
total de filhos igualmente entre as mulheres,
cada uma delas não chega a ter 2 filhos.

7. Vale salientar que a média também é adequada
para algumas situações com variáveis
quantitativas, como o número de calçado mais
usado por um grupo de pessoas.

8. Média ponderada
A média ponderada é calculada por meio do
somatório das multiplicações entre valores e
pesos divididos pelo somatório dos pesos.
A média ponderada leva em consideração o
peso de cada informação no cálculo, seja ele um
valor atribuído, seja uma quantidade. E é
atribuído aos valores importâncias diferentes.

9. Exemplo:
Buscando melhorar o atendimento ao usuário
do sistema de saúde de um município, realizou-
se uma pesquisa de rendimento satisfatório com
500 pessoas. As notas disponibilizadas aos
entrevistados no intuito de avaliar o nível de
satisfação compreendem as notas inteiras de 1 a
10. Veja os resultados na tabela a seguir:

10. b

11. Mp =
1•5+2•15+3•40+4•128+5•150+6•90+7•35+8•25+9•10+10•2
5+15+40+128+150+90+35+25+10+2
Mp= 5+30+120+512+750+540+245+200+90+20
500
=
2512
500
= 5,024
A média de satisfação dos usuários do sistema de
saúde do município em questão foi igual a 5,0.

12. Moda de um conjunto de dados é aquele valor que
ocorre com maior frequência. É especialmente útil
quando a amplitude de valores possíveis é menor.
Representa-se por Mo.
Por exemplo:
Foi feita uma pesquisa sobre a frequência de um grupo
de alunos em relação ao curso superior que desejariam
cursar ao concluir o nível médio. Veja a tabela a seguir:

13. Como vê, existe um curso mais citado. Esse curso mais citado foi o de
Engenharia (citado duas vezes), os demais foram citados apenas uma
vez. Por isso, a opção “Engenharia” é a moda desse conjunto, o valor
dominante ou valor típico nesse grupo.
Há casos em que nenhum número se repete em nenhuma vez,
portanto dizemos que esse conjunto não possui moda ou, em outras
palavras, chamamos ele de Amodal.
Aluno Curso
Daniel Medicina
Lúcia Direito
Romeu Engenharia
Bianca Biologia
Denilson Engenharia

14. Classificações da moda:
É importante que você saiba que a moda, em um conjunto, pode
assumir quatro classificações possíveis. A seguir irei apresentar essas
classificações e suas principais características:
Amodal, quando não existe moda.
Exemplo: A={7,5,4,8,3}
Unimodal, quando há apenas uma única moda.
Exemplo: B={8,6,8,5,1,4,7,8}
Moda = 8
Bimodal, quando há exatamente duas modas.
Exemplo: C={8,6,4,5,1,15,4,7,8}
Moda = 4 e 8
Multimodal, quando há três ou mais modas.
Exemplo: D={9,1,8,5,1,4,8,5,7,12}
Moda= 1, 5 e 8

15. A moda pode ser utilizada para representar
tanto um conjunto de dados numéricos como
um conjunto de dados nominais.
No primeiro exemplo sobre a moda, tinha se
destacado entre os demais naquela pesquisa, o
curso de engenharia.
Aquele conjunto formado pelos nomes dos
cursos é um exemplo de conjunto nominal, ou
seja, um conjunto formado apenas por nomes.

16. Mediana de um conjunto o separa em duas
partes de modo que 50% dos valores sejam
menores que ela e 50% dos valores sejam
maiores que ela, ou seja, em um conjunto onde
seus elementos estão dispostos em ordem
crescente ou decrescente a mediana é o termo
central desse conjunto ou o elemento que está
bem no meio.

17. Por exemplo: Considere um conjunto A, tal
que: A={6,4,2,7,8,4}. Em primeiro lugar
colocamos esse conjunto em ordem
crescente ou decrescente.
Geralmente costuma-se colocar sempre na
ordem crescente para melhor entendimento do
assunto. Logo o conjunto A ficará da seguinte
maneira:
A={2,4,4,6,7,8}

18. Quando há um número ímpar de termos em um
conjunto, existirá um único termo central.
Nesses casos a mediana será o próprio termo
central, sem dificuldades.
Exemplo: Considerando um
conjunto B={5,7,9,1,2,2,6} determinar
a mediana desse conjunto. Primeiro devemos
organizar esse conjunto em ordem crescente ou
decrescente, conforme a sua preferência. Em
ordem crescente o conjunto ficaria assim:
B={1,2,2,5,6,7,9}

19. Neste caso o termo central é o que se encontra
na 4ª posição, ou seja, o número 5. Dizemos
então que o número 5 é a mediana desse
conjunto pois é ele que se encontra bem no
centro dele.
Caso o conjunto tenha um número par de
termos, a mediana será a média aritmética dos
dois termos centrais.

20. Exemplo:
C={5,1,2,6, 3,2,7,9}
Em ordem crescente o conjunto ficaria assim:
B={1,2,2,3,5,6,7,9}
Neste caso os termos centrais são so que se
encontram na 4ª e 5ª posição, os números 3 e 5.
Então a mediana será a média aritmética destes
dois números
3+5
2
=4. Logo, a mediana é igual a 4.