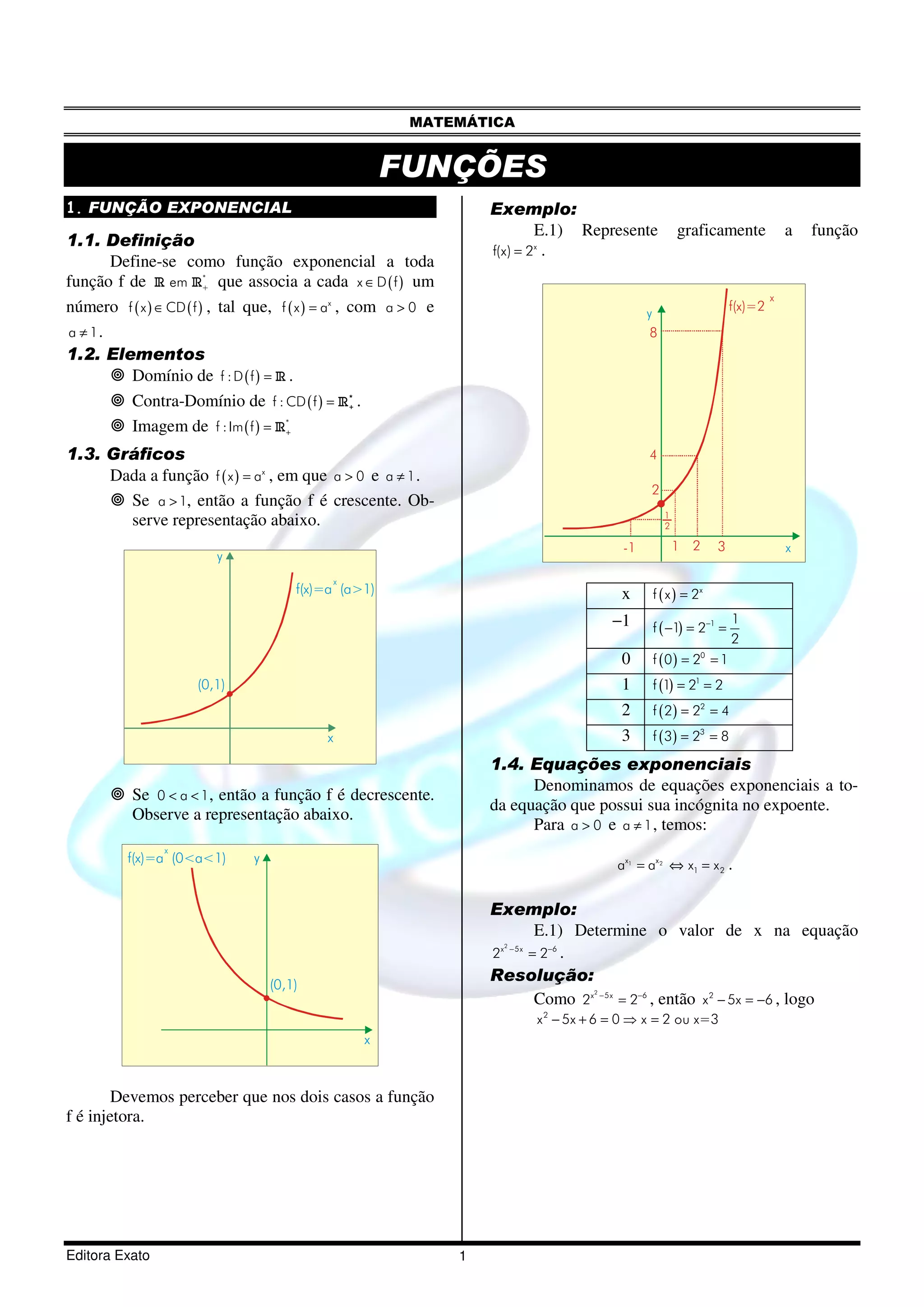
Este documento trata de funções exponenciais e equações exponenciais. Ele define funções exponenciais, mostra seus elementos e gráficos quando a > 1 ou 0 < a < 1. Também apresenta exemplos de equações exponenciais e como resolvê-las. Por fim, contém exercícios resolvidos sobre o assunto.