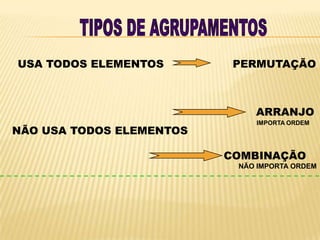
Análise combinatória estuda os agrupamentos de elementos sem enumerá-los. É importante para estimativas em jogos de azar e planejamento de horários e produção, entre outros usos. O princípio fundamental de contagem estabelece que, se um evento pode ocorrer em etapas independentes, o número de possibilidades é o produto das possibilidades de cada etapa.

1. ANÁLISE
COMBINATÓRIA
1

2. ANÁLISE COMBINATÓRIA é uma
parte da matemática que estuda os
agrupamentos de elementos sem
precisar enumerá-los.
2

3. Atualmente, a estimativa de acertos
em jogos populares como: loteria
esportiva, loto, loteria federal, etc.,
além de utilizações mais específicas,
como confecções de horários, de
planos de produção, de números de
placas de automóveis etc.
3

4. POR QUE É IMPORTANTE CONHECER UM PROCESO
DE CONTAGEM?
 É importante conhecermos tais métodos,
pois nem sempre temos condições de
descrever todas as formas sob as quais uma
situação pode ocorrer, principalmente em
situações onde a resposta é um número
muito elevado.

5. PRINCÍPIO FUNDAMENTAL DE CONTAGEM
 01. Uma moça possui 5 camisas e 4 saias, de
quantas maneiras ela poderá se vestir?
 A escolha de uma camisa poderá ser feita de
cinco maneiras diferentes. Escolhida a primeira
camisa poderá escolher uma das quatro saias.
Portanto, o número total de escolhas será: 4 x
5 = 20
5

6. PODEMOS ENUNCIAR O PFC DA SEGUINTE MANEIRA:
 Se um evento pode ocorrer por várias etapas
sucessivas e independentes, de tal modo que:
P1 é o número de possibilidades da etapa 1;
P2 é o número de possibilidades da etapa 2;
Pn é o número de possibilidades da etapa n.
O número de maneiras que o evento pode ocorrer
é dado por: p1.p2.p3...pn.

7. O PRINCÍPIO ADITIVO
Tal princípio trabalha com eventos independentes. Em
outras palavras quanto temos a opção de escolher uma
coisa ou outra.
De maneira geral temos que: Se existem x maneiras de se
tomar uma decisão A e y maneiras de se tomar uma
decisão B, o número de opções de se tomar a decisão A
ou a B será dada por x + y.

8. Observe que quanto usamos o termo
“ou” em Análise Combinatória,
devemos somar as possibilidades dos
eventos e quando usamos o termo “e”,
devemos multiplicar o número de
possibilidades.

9. Arranjo Simples
n!
A n.p =
(n - p)!
9

10. Permutação simples
Pn = n!
Permutação com repetição
n!
P
 !  ! !
10

11. Combinação simples
n!
Cn.p =
(n - p)! . p!
11

12. Permutação Circular
P = ( n – 1)!
12

13. USA TODOS ELEMENTOS PERMUTAÇÃO
ARRANJO
IMPORTA ORDEM
NÃO USA TODOS ELEMENTOS
COMBINAÇÃO
NÃO IMPORTA ORDEM