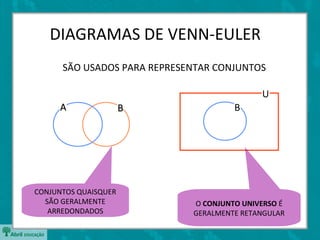
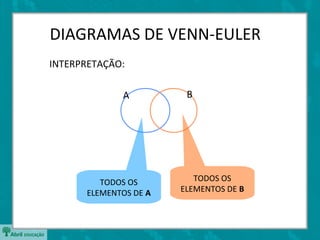
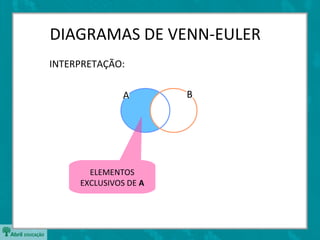
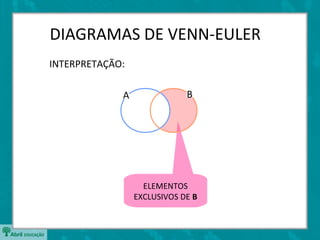
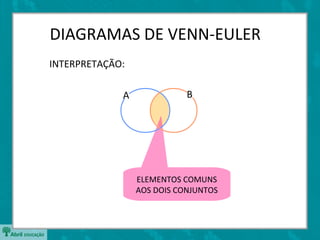
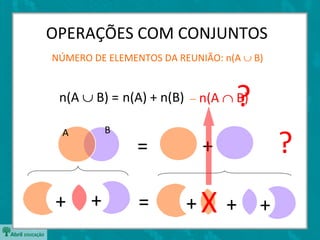
O documento apresenta os diagramas de Venn-Euler, que são usados para representar conjuntos através de círculos sobrepostos. Apresenta as operações básicas com conjuntos como união, interseção e diferença. Explica que o número de elementos da união de dois conjuntos é dado pela soma dos elementos individuais menos os elementos em comum entre os conjuntos.

1. OPERAÇÕES
COM
CONJUNTOS

2. DIAGRAMAS DE
VENN-EULER

3. DIAGRAMAS DE VENN-EULER
[1] [2]
JOHN VENN, LEONHARD EULER,
1834-1923 1707-1783
[1] Charles E. Brock/ Cortesia de Master and Fellows of Gonville and Caius College/ foto: Christopher Hust, Hamilton Kerr Institute, University of Cambridge
[2] Johann Georg Brucker/ Wapedia.com

4. DIAGRAMAS DE VENN-EULER
[1]
Janela da Faculdade Gonville e
Caius (Universidade Cambridge)
Homenageando John Venn,
estudante e professor da
instituição.
[1] Wikimédia commons/arquivo da editora

5. DIAGRAMAS DE VENN-EULER
SÃO USADOS PARA REPRESENTAR CONJUNTOS
U
A B B
CONJUNTOS QUAISQUER
SÃO GERALMENTE O CONJUNTO UNIVERSO É
ARREDONDADOS GERALMENTE RETANGULAR

6. DIAGRAMAS DE VENN-EULER
INTERPRETAÇÃO:
A B
TODOS OS TODOS OS
ELEMENTOS DE A ELEMENTOS DE B

7. DIAGRAMAS DE VENN-EULER
INTERPRETAÇÃO:
A B
ELEMENTOS
EXCLUSIVOS DE A

8. DIAGRAMAS DE VENN-EULER
INTERPRETAÇÃO:
A B
ELEMENTOS
EXCLUSIVOS DE B

9. DIAGRAMAS DE VENN-EULER
INTERPRETAÇÃO:
A B
ELEMENTOS COMUNS
AOS DOIS CONJUNTOS

10. OPERAÇÕES COM
CONJUNTOS

11. OPERAÇÕES COM CONJUNTOS
UNIÃO OU REUNIÃO: A ∪ B
B U
A A ∪ B = {x|x∈A ou x∈B}
{ 1, 3, 5 } ∪ { 2, 4, 6} = {1, 2, 3, 4, 5, 6}
{ 1, 3, 5} ∪ { 2, 4, 5, 6} = {1, 2, 3, 4, 5, 6}
{ 1, 3, 5} ∪ { 1, 2, 3, 4, 5, 6} = {1, 2, 3, 4, 5, 6}

12. OPERAÇÕES COM CONJUNTOS
INTERSECÇÃO: A ∩ B
U
A B A ∩ B = {x|x∈A e x∈B}
{ 1, 3, 5 } ∩ { 2, 4, 6} = ∅
{ 1, 3, 5} ∩ { 2, 4, 5, 6} = {5}
{ 1, 3, 5} ∩ { 1, 2, 3, 4, 5, 6} = {1, 3, 5}

13. OPERAÇÕES COM CONJUNTOS
DIFERENÇA: A − B
U
B A − B = {x|x∈A e x∉B}
A
DIFERENÇA: B − A
U
A B B − A = {x|x∈B e x∉A}

14. OPERAÇÕES COM CONJUNTOS
DIFERENÇA: A − B
U
A B A − B = {x|x∈A e x∉B}
{ 1, 3, 5 } − { 2, 4, 6} = {1, 3, 5}
{ 1, 3, 5} − { 2, 4, 5, 6} = {1, 3}
{ 1, 3, 5} − { 1, 2, 3, 4, 5, 6} = ∅

15. OPERAÇÕES COM CONJUNTOS
C
A
COMPLEMENTAR: U ou A ou AC
(SÓ TEM SENTIDO QUANDO FIXAMOS UM CONJUNTO UNIVERSO U)
U
A
C
A = {x|x∈U e x∉A} = U − A

16. NÚMERO DE ELEMENTOS DA
REUNIÃO DE CONJUNTOS

17. OPERAÇÕES COM CONJUNTOS
NÚMERO DE ELEMENTOS DA REUNIÃO: n(A ∪ B)
n(A ∪ B) = n(A) + n(B) − ?
n(A ∩ B)
?
A B
= +
+ + = +X + +

18. OPERAÇÕES COM CONJUNTOS
NÚMERO DE ELEMENTOS DA REUNIÃO: n(A ∪ B)
n(A ∪ B) = n(A) + n(B) − n(A ∩ B)

19. FIM