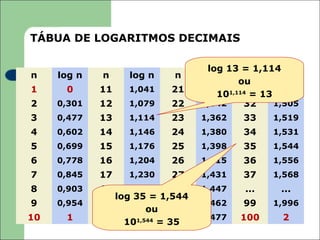
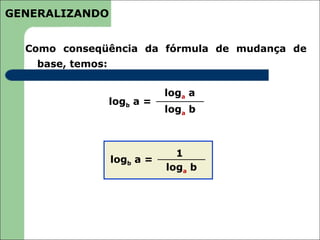
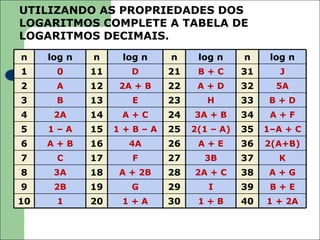
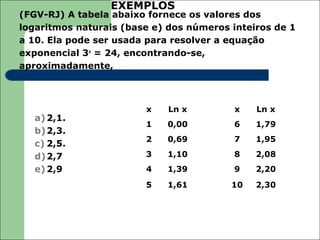
O documento apresenta uma introdução aos logaritmos, definindo-os como o expoente ao qual uma base deve ser elevada para se obter um determinado número. Explica que os logaritmos decimais utilizam a base 10 e foram introduzidos por Henry Briggs para simplificar cálculos numéricos.

1. LOGARITMOS
Ângelo Moreira dos Reis

2. QUAL É O TEMPO?
Giovanna ganhou 1 000 reais de seu pai pra fazer
sua festa de 15 anos. Ao receber o dinheiro, no
entanto, resolveu abrir mão da festa. É que ela
queria comprar um computador.
Mas havia um problema: o computador que ela
queria custava 1 500 reais. O jeito era aplicar o
dinheiro que tinha, até conseguir o valor
necessário.

3. QUAL É O TEMPO?
Giovanna foi ao banco e conseguiu uma taxa de
5 % ao mês, capitalizados mensalmente.
Chegando em casa, ficou curiosa. Em quanto
tempo os 1000 reais aplicados se transfor-
mariam nos 1500 reais de que precisava?
Ela havia acabado de aprender a calcular juros
compostos. Fez, então, as suas contas.

4. VEJA OS CÁLCULOS
Capital aplicado: C = 1 000
Taxa: 5 % ao mês = 0,05 ao mês
Montante pretendido: M = 1 500,00
M = C.(1 + i)t ⇒ 1 500 = 1 000 . (1,05)t
1,057 ≈ 1,407
⇒ 1,05t = 1,5 1,058 ≈ 1,477
1,059 ≈ 1,551
Giovanna concluiu, portanto, que seu objetivo seria
atingido no final do 9º mês de aplicação.

5. QUAL É O EXPOENTE?
Como poderia ser obtido, com uma aproximação
razoável e sem utilizar o método das tentativas,
o valor de t na equação 1,05t = 1,5?
A teoria dos logaritmos é muito útil em problemas
como esse, que envolve a determinação de um
expoente.

6. HISTÓRIA
A invenção dos logaritmos ocorreu no início do
século XVII e é creditada ao escocês John
Napier e ao suiço Jobst Burgi.
Inicialmente seu objetivo era simplificar os
cálculos numéricos, principalmente em
problemas ligados à Astronomia e à Navegação.

7. HISTÓRIA
A partir dessa fabulosa invenção, tornaram-se
mais simples e mais ágeis cálculos de
expressões como
2,382,5 . √12,4
3
5,13,8
O valor dessa expressão equivale ao valor de
102,5.log 2,38 + (1/3).log 12,4 – 3,8.log 5,1

8. HISTÓRIA
Foi o matemático inglês Henry Briggs (1561 –
1631) quem propôs, inicialmente, a utilização do
sistema de logaritmos decimais. Afinal, o nosso
sistema de numeração utiliza justamente a base
10.

9. HISTÓRIA
Atualmente, são inúmeras as aplicações
tecnológicas dos logaritmos. Eles são úteis, por
exemplo, na resolução de problemas que
envolvem desintegração radiotiva, o
crescimento de uma população de animais ou
bactérias, etc.

10. TRABALHANDO COM
POTÊNCIAS DE BASE
10

11. A BASE 10
Todo número positivo pode ser escrito como uma
potência de base 10, ou como uma aproximação
dessa potência. Veja os exemplos:
1 = 100 0,1 = 10–1
10 = 101 0,01 = 10–2
100 = 102 0,001 = 10–3
1 000 = 103 0,0001 = 10–4
10 000 = 104 0,00001 = 10–5

12. A BASE 10
Na maioria dos casos, torna-se difícil escrever um
número como potência de base 10. Em valores
aproximados apresentamos os exemplos:
2 = 100,301
3 = 100,477
7 = 100,845
11 = 101,041
13 = 101,114

13. EXEMPLOS
Usando as igualdades 2 = 100,301 e 3 = 100,477, escreva
os números 4, 5 e 6 como potência de base 10.
 4 = 22 = (100,301)2 = 100,602
 5 = 10 = 10 = 100,699
= 101 – 0,301
2 100,301
 6 = 2.3 = 100,301 . 100,477 = 100,301 + 0,477
= 100,778

14. EXEMPLOS
Usando as igualdades 2 = 100,301 e 3 = 100,477, escreva
o número 60 como potência de base 10.
 60 = 2.3.10 = 100,301 . 100,477 . 10
⇒ 60 = 100,301 + 0,477 + 1
⇒ 60 = 101,778

15. EXEMPLOS
Usando as igualdades 2 = 100,301 e 3 = 100,477, resolva
a equação exponencial 2x = 12.
2x = 12 ⇒ 2x = 22.3
⇒ (100,301)x = (100,301)2 . 100,477
⇒ 100,301.x = 100,602 . 100,477
⇒ 100,301.x = 101,079 ⇒ 0,301.x = 1,079
1,079
⇒ x= ⇒ x ≈ 3,585
0,301

16. LOGARITMO
COMO
EXPOENTE

17. LOGARITMO COMO EXPOENTE
O conceito de logaritmo está associado à operação
potenciação: mais precisamente à determinação
do expoente. Veja:
2x = 8 ⇒ x = 3
No caso, dizemos, que o logaritmo de 8, na base 2 ,
é igual ao expoente 3. Em símbolos,
log2 8 = 3

18. LOGARITMO COMO EXPOENTE
Observe: calcular o log2 8 é descobrir o expoente
ao qual se deve elevar a base 2, para obter,
como resultado, a potência 8.
Vale, portanto a equivalência:
log2 8 = 3 ⇔ 23 = 8
Calcular um logaritmo é obter um expoente.
Logaritmo é o mesmo que expoente.

19. DEFINIÇÃO
Suponhamos dois reais positivos a e b (a ≠ 1). Se
ax = b, dizemos que x é o logaritmo de b na base
a (simbolicamente loga b = x).
loga b = x ⇔ ax = b
 a é a
base;
 b é o logaritmando ou antilogaritmo;
 x é o logaritmo;

20. EXEMPLOS
 log2 32 = 5, porque 25 = 32
 log3 (1/81) = –4, porque 3–4 = 81
 log10 0,001 = –3, porque 10–3 = 0,001
3 3
 log5 √25 = 2/3, porque 5 2/3
= √252
De acordo com a definição, calcular um logaritmo
é descobrir o expoente, ou seja, resolver uma
equação exponencial.

21. EXEMPLOS
 Calcular log4 8.
log4 8 = x ⇒ 4x = 8 ⇒ (22)x = 23
⇒ 22x = 23 ⇒ x=3

22. EXEMPLOS
 Calcular log1/3 √9.
5
x
1 5
5
⇒ = √9
log1/3 √9 = x 3
⇒ (3–1)x = 32/5 ⇒ 3–x = 32/5
⇒ –x = 2/5
⇒ x = –2/5

23. CONDIÇÃO DE EXISTÊNCIA DO
LOGARITMO
Da definição, concluímos que o logaritmo só existe
sob certas condições:
b>0
loga b = x ⇔ a>0
a≠ 1

24. CONDIÇÃO DE EXISTÊNCIA
 Analise quais seriam os significados de log2 (–4),
log(–2) 8, log7 0, log1 6 e log0 2, caso fossem
definidos.
log2 (–4) = x ⇒ 2x = –4 impossível
log–2 8 = x ⇒ (–2)x = 8 impossível
log7 0 = x ⇒ 7x = 0 impossível
log1 6 = x ⇒ 1x = 6 impossível
log0 2 = x ⇒ 0x = 2 impossível

25. OBSERVAÇÃO
Muitas vezes, um logaritmo envolve variáveis.
Nesse caso, devemos analisar o domínio dessas
variáveis. Para isso, usamos as condições de
existência do logaritmo.

26. EXEMPLOS
 Resolver a equação logx (2x + 8) = 2.
1o. Vamos analisar a condição de existência do logaritmo.
2x + 8 > 0 x > –4
x>0
x>0 ⇒ x>0 ⇒
x≠1
x≠1 x≠1
2o. Usando a definição de logaritmo.
logx (2x + 8) = 2 ⇒ x2 = 2x + 8 ⇒ x2 – 2x – 8 = 0
⇒ x = –2 ou x = 4. ⇒ S = {4}

27. CONSEQÜÊNCIA
S DA
DEFINIÇÃO

28. CONSEQÜÊNCIAS DA DEFINIÇÃO
Admitindo-se válidas as condições de existência
dos logaritmos, temos os seguintes casos
especiais, que são conseqüências da definição.
loga 1 = 0 porque a0 = 1
loga a = 1 porque a1 = a
loga ak = k porque ak = ak

29. EXEMPLOS
 log3 3 = log10 10 = log3,7 3,7 = 1
 log3 1 = log10 1 = log3,7 1 = 0
 log3 39 = 9
 log10 10–3 = –3

30. CONSEQÜÊNCIAS DA DEFINIÇÃO
Sabemos que loga k é o expoente ao qual se deve
elevar a base a para se obter k. Vale por isso, a
seguinte igualdade:
loga k
a =k

31. EXEMPLOS
log5 3
 5 =3
1 + log2 6 log2 6
 2 = 2 .2 1
= 2.6 = 12
log3 5 log3 5
 9 log3 5 2
= (32) = 3 = 52 = 25
1 – log15 3 151 15
 15 = = =5
log15 3 3
15

32. SISTEMA DE
LOGARITMOS

33. SISTEMA DE LOGARITMOS
Sistema de logaritmos é o conjunto de todos os
logaritmos numa determinada base. Entre os
infinitos sistema de logaritmos, destacam-se dois:
O sistema de logaritmos decimais utiliza a base 10.
No cálculo de logaritmos decimais, convenciona-se
não escrever a base, ou seja, log x é o mesmo que
log10 x.
log x → logaritmo decimal de x (base 10)

34. EXEMPLOS
 log 1000 = log10 1000 = 3
 log 0,01 = log10 10–2 = –2
 log 1 = log10 1 = 0
 log 100 = log10 100 = 2

35. SISTEMA DE LOGARITMOS
O sistema de logaritmos naturais ou neperianos,
utiliza, como base, o número irracional e.
Esse número foi introduzido por Euler, em meados do
século XVIII. Seu valor aproximado é e=
2,71828.
O logaritmo natural de um número x pode ser
indicado por Ln x.
Ln x → logaritmo natural de x (base e)

36. EXEMPLOS
 Ln e = loge e = 1
 Ln 10 = loge 10 ≈ 2,3
 Ln e3 = loge e3 = 3

37. OBSERVAÇÃO
Chama-se co-logaritmo de a na base b (em
símbolos, cologb a) o oposto do logaritmo de a
na base b.
cologb a = – logb a
 colog2 8 = – log2 8 = –3
 colog3 (1/9) = – log3 (1/9) = 2

38. LOGARITMOS
DECIMAIS

39. LOGARITMOS DECIMAIS
O primeiro a utilizar os logaritmos decimais foi o
matemático inglês Henry Briggs (1561-1631).
Foi ele quem construiu a primeira tábua de
logaritmos decimais.

40. TÁBUA DE LOGARITMOS DECIMAIS
log 13 = 1,114
n log n n log n n log n n log n
ou
1 0 11 1,041 21 31
1,322 1,114 1,491
10 = 13
2 0,301 12 1,079 22 1,342 32 1,505
3 0,477 13 1,114 23 1,362 33 1,519
4 0,602 14 1,146 24 1,380 34 1,531
5 0,699 15 1,176 25 1,398 35 1,544
6 0,778 16 1,204 26 1,415 36 1,556
7 0,845 17 1,230 27 1,431 37 1,568
8 0,903 18 1,255 28 1,447 ... ...
log 35 = 1,544
9 0,954 19 1,279 29 1,462 99 1,996
ou
10 1 20 1,301 30 1,477 100 2
101,544 = 35

41. EXEMPLOS
 Calcule os logaritmos decimais
a) log 10
b) log 10 000
c) log 1013
d) log 10–30
e) log 0,000001

42. EXEMPLOS
 Consultando a tábua de logaritmos calcule
a) log 60 + log 31 – log 5
b) 100,903 + 101,505 – 1000,69
c) os valores de x e y tais que 10x = 26 e
1000y = 15

43. EXEMPLOS
 Em valores aproximados, a tábua de logaritmos
mostra que log 13 = 1,114 ou 101,114 = 13. A partir
desses valores, sem uso de calculadora, obtenha
os números seguintes.
a) 102,114; 104,114; 100,114 e 1001,557.
b) log 130; log 13000; log 1,3 e log 1300
c) os valores de x e y tais que 10x = 0,13 e
13y = 103,342.

44. MUDANÇA DE
BASE

45. MUDANÇA DE BASE
Observe uma calculadora científica. Ela permite o
cálculo apenas dos logaritmos decimais (tecla
log) e dos logaritmos naturais (tecla Ln).
Como obter então, numa calculadora, logaritmos
em outras bases?
Será possível achar, por exemplo, os valores de
log3 5 e log7 23?

46. MUDANÇA DE BASE
Na tábua de logaritmos decimais, encontramos
que log10 23 = 1,362 e log10 7 = 0,845. A partir
deles, determine o valor log7 23.
log10 23 = 1,362 ⇒ 101,362 = 23
log10 7 = 0,845 ⇒ 100,845 = 7 log10 23
log7 23 =
log10 7
log7 23 = x ⇒ 7x = 23
⇒ (100,845)x = 101,362 ⇒ 100,845.x = 101,362
1,362
⇒ 0,845.x = 1,362 ⇒ x= = 1,612
0,845

47. FÓRMULA DE MUDANÇA DE BASE
De modo geral, podemos calcular logba, utilizando
uma outra base k arbitrária. Para isso, dividimos
o logaritmo de a pelo logaritmo de b, na base k
escolhida. logk a
Logb a =
logk b

48. EXEMPLOS
 Pela tecla Ln (logaritmo natural) de uma
calculadora, obtemos Ln 6 = 1,792 e Ln 2 = 0,693.
A partir desses valores, calcular log2 6.
loge 6 Ln 6 1,792
log2 6 = = = = 2,586
loge 2 Ln 2 0,693

49. EXEMPLOS
 Resolver a equação 5x = 20, dados os logaritmos
decimais log 5 = 0,699 e log 20 = 1,301.
5x = 20 ⇒ x = log5 20
log10 20 log 20 1,301
log5 20 = = = = 1,861
log10 5 log 5 0

50. EXEMPLOS
 Se logk x = 2, calcular logx (1/k).
logk (1/k) –1
logx (1/k) = =
logk x 2

51. EXEMPLOS
 Se log 2 = 0,30 e log 3 = 0,48, calcular log2 3.
1o. Vamos a fórmula de mudança de base.
log 3 0,48
log2 3 = = = 1,6
log 2 0,30
Observe que, log2 3 = 1,6 ⇔ 21,6 = 3.

52. EXEMPLOS
 Escrevendo os logaritmos numa mesma base,
obtenha o valor mais simples do produto
log2 7 . Log7 13 . Log13 2
1o. Vamos a fórmula de mudança de base.
1 1 1
log 7 . log 13 . log 2 = 1
log 2 log 7 log 13
1 1 1

53. CONSEQÜÊNCIA – MUDANÇA DE BASE
 Compare os valores dos log5 25 e log25 5.
log5 25 = 2 e log25 5 = 1/2
 Compare, também, os valores log2 8 e log8 2.
log2 8 = 3 e log8 2 = 1/3
 Que conclusão se pode tirar dessas comparações?
logb a = 1/loga b
 Se logx y = 3/5, calcule logy x.
logy x = 5/3

54. GENERALIZANDO
Como conseqüência da fórmula de mudança de
base, temos:
loga a
logb a =
loga b
1
logb a =
loga b

55. PROPRIEDADE
S DOS
LOGARITMOS

56. PROPRIEDADES DOS LOGARITMOS
O logaritmo tem uma particularidade importante. Ele
transforma operações mais complicadas em
operações mais simples.
Com as propriedades dos logaritmos podemos
transformar:
 multiplicações em adições;
 divisões em subtrações;
 potenciações em multiplicações;
 radiciações em divisões.

57. LOGARITMO DO PRODUTO
Vamos calcular o valor do log 21, a partir dos
valores de log 3 = 0,477 e log 7 = 0,845.
log 3 = 0,477 ⇒ 100,477 = 3
log 7 = 0,845 ⇒ 100,845 = 7
log 21 =⇒ 10x = 21 log 3 + log 7
log 21 = x log (3.7) =
⇒ 10x = 3.7 ⇒ 10x = 100,477.100,845
⇒ 10x = 100,477 + 0,845
⇒ x = 0,477 + 0,845 ⇒ x = 1,322

58. LOGARITMO DO PRODUTO
De modo geral, o logaritmo do produto de dois
números, numa certa base, é a soma dos
logaritmos desses números, na mesma base.
Loga (x.y) = loga x + loga y
Para o produto de três ou mais fatores, a propriedade
continua válida.

59. EXEMPLOS
A par tir de log 2 = 0,301 e log 13 = 1,114, calcular log 26 e log 2000.
 log 26 = log (2.13) = log 2 + log 13
log 26 = 0,301 + 1,114 = 1,415
 log 2000 = log (2.1000) = log 2 + log 1000
log 2000 = 0,301 + 3 = 3,301

60. EXEMPLOS
Sendo x e y reais positivos, decompor log3 (9xy)
numa soma de logaritmos.
log3 (9xy) = log3 9 + log3 x + log3 y
log3 (9xy) = 2 + log3 x + log3 y

61. EXEMPLOS
Transformar num único logaritmo e calcular o
valor da expressão log 4 + log 5 + log 50.
log 4 + log 5 + log 50 = log (4.5.50)
log 4 + log 5 + log 50 = log 1000 = 3

62. LOGARITMO DO QUOCIENTE
Vamos calcular o valor do log (3/2), a partir dos
valores de log 2 = 0,301 e log 3 = 0,477.
log 2 = 0,301 ⇒ 100,301 = 2
log 3 = 0,477 ⇒ 100,477 = 3
log (3/2) = x ⇒ (3/2) =
log 10x = 3/2 log 3 – log 2
3 100,477
⇒ 10 =
x
= = 100,477 – 0,301
2 100,301
⇒ x = 0,477 – 0,301 ⇒ x = 0,176

63. LOGARITMO DO QUOCIENTE
De modo geral, o logaritmo do quociente de dois
números, numa certa base, é a diferença dos
logaritmos desses números, na mesma base.
Loga x = loga x – loga y
y

64. EXEMPLOS
A partir de log 2 = 0,301 obter log 5.
10
log 5 = log = log 10 – log 2 = 1 – 0,301
2
⇒ log 5 = 0,699

65. EXEMPLOS
Se x e y são reais positivos, decompor em parcelas
log2 (x/4y).
x
log2 = log2 x – log2 4y
4y
= log2 x – (log2 4 + log2 y)
= log2 x – (2 + log2 y)
= log2 x – 2 – log2 y
= log2 x – log2 y – 2

66. EXEMPLOS
Compor (transformar num único logaritmo) a
expressão E = log m – log 3 + 2 – log n.
1º. Vamos transformar a parcela 2 na forma de logaritmo
decimal. log 100 = 2.
E = log m – log 3 + log 100 – log n
E = (log m + log 100) – (log 3 + log n)
E = (log 100m) – (log 3n)
100m
E = log
3n

67. LOGARITMO DA POTÊNCIA
Vamos calcular o valor do log 34, a partir do valor
de log 3 = 0,477.
log 3 = 0,477 ⇒ 100,477 = 3
log 34 = x ⇒ 10x = 34 ⇒ 10x = (100,477)4
⇒ x = 4 . 0,477 ⇒ x = 1,908
log 34 = 4 . log 3

68. LOGARITMO DA POTÊNCIA
Generalizando, o logaritmo de uma potência, é
igual ao produto do expoente da potência pelo
logaritmo da base.
Loga xk = k . loga x

69. EXEMPLOS
A partir do log 3 = 0,477, calcular log 0,009.
9
log 0,009 = log = log 9 – log 100
100
= log 32 – 2 = 2 . log 3 – 2
= 2 . 0,477 – 2
= 0,954 – 2 = – 1,046

70. EXEMPLOS
13√3
Calcular log 4 , a partir dos valores log 2 =
0,301, log 3 = 0,477 e log 13 = 1,114.
13√3
log = log 13 + log √3 – log 4
4
= log 13 + log 31/2 – log 22
= log 13 + 1 . log 3 – 2 . log 2
2
= 1,144 + 0,5.0,477 – 2.0,301
= 1,144 + 0,2385 – 0,601 = 0,7505

71. EXEMPLOS
Compor e simplificar a expressão
1
E = 2.log3 12 – 3 log3 8 – 2
1º. Vamos transformar a parcela 2 na forma de logaritmo
de base 3. (log3 9 = 2).
1
E = 2.log3 12 – log3 8 + log3 9
3
E = log3 122 – log3 81/3 + log3 9
E = log3 144 – log3 2 + log3 9 = log3 144 – log3 (2.9)
144
E = log3 144 – log3 18 ⇒ E = log3 = log3 8
18

72. UTILIZANDO AS PROPRIEDADES DOS
LOGARITMOS COMPLETE A TABELA DE
LOGARITMOS DECIMAIS.
n log n n log n n log n n log n
1 0 11 D 21 B+C 31 J
2 A 12 2A + B 22 A+D 32 5A
3 B 13 E 23 H 33 B+D
4 2A 14 A+C 24 3A + B 34 A+F
5 1–A 15 1+B–A 25 2(1 – A) 35 1–A + C
6 A+B 16 4A 26 A+E 36 2(A+B)
7 C 17 F 27 3B 37 K
8 3A 18 A + 2B 28 2A + C 38 A+G
9 2B 19 G 29 I 39 B+E
10 1 20 1+A 30 1+B 40 1 + 2A

73. EXEMPLOS
(FGV-RJ) A tabela abaixo fornece os valores dos
logaritmos naturais (base e) dos números inteiros de 1
a 10. Ela pode ser usada para resolver a equação
exponencial 3x = 24, encontrando-se,
aproximadamente,
x Ln x x Ln x
a) 2,1.
1 0,00 6 1,79
b) 2,3.
2 0,69 7 1,95
c) 2,5.
d) 2,7 3 1,10 8 2,08
e) 2,9 4 1,39 9 2,20
5 1,61 10 2,30

74. EXEMPLOS
Se log 2 = a e log 3 = b, escreva o log2 72 em
função de a e b.
log 72 log 23.32
log2 72 = =
log 2 log 2
log 23 + log 32 3.log 2 + 2.log 3
= =
log 2 log 2
3a + 2b
=
a