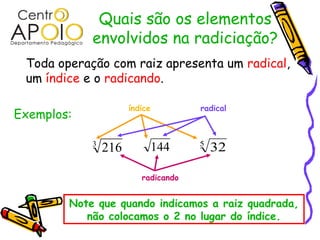
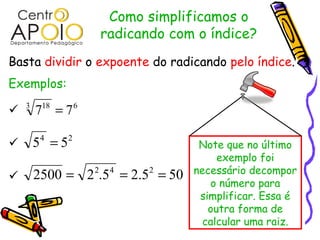
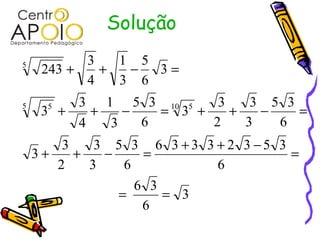
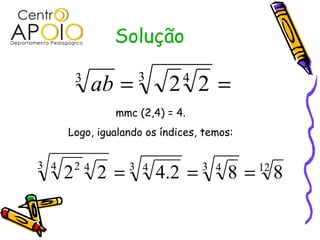O documento aborda conceitos fundamentais de radiciação, incluindo a identificação de elementos como radical, índice e radicando, além de descrever a relação entre radiciação e potenciação. Ele também explica como calcular raízes, simplificar radicais, somar, subtrair, multiplicar e dividir radicais, e os métodos para racionalizar denominadores. Os procedimentos e exemplos práticos são apresentados para facilitar a compreensão das regras e propriedades da radiciação.

1. RadiciaçãoRadiciação

2. Ao final dessa aula
você saberá:
Identificar os elementos envolvidos em na
radiciação
Relacionar potências e raízes
Calcular uma raiz de 2 formas diferentes
Todas as regras e propriedades da radiciação
Somar, subtrair, multiplicar e dividir radicais
Elevar um radical a uma potência e extrair sua
raiz.
Racionalizar denominadores

3. Quais são os elementos
envolvidos na radiciação?
Toda operação com raiz apresenta um radical,
um índice e o radicando.
Exemplos:
3
216 144 5
32
índice radical
radicando
Note que quando indicamos a raiz quadrada,
não colocamos o 2 no lugar do índice.

4. Qual é a relação entre
radiciação e potenciação?
A radiciação é a operação inversa da
potenciação.
Exemplos:
39 =
51253
=
32
= 9
53
= 125

5. Por que não existe raiz com
índice par de um número
negativo no conjunto real?
Porque não existe um número que, elevado
a expoente par, tenha como resultado um
número negativo.
Veja: 9−
Não existe um número que
elevado ao quadrado dá -9,
pois -3 e 3 elevado ao
quadrado dá 9.

6. Como calculamos raiz de
um número grande?
Usando a decomposição em fatores primos.
Exemplos: 448 3
3375
2
2
2
1
448 2
224 2
112 2
56 2
28 2
14 2
7 7
78=448
3375 3
1125 3
375 3
125 5
25 5
5 5
1
3
5
1553506253
== x

7. Como simplificamos o
radicando com o índice?
Basta dividir o expoente do radicando pelo índice.
Exemplos:



24
55 =
63 18
77 =
505.25.22500 242
===
Note que no último
exemplo foi
necessário decompor
o número para
simplificar. Essa é
outra forma de
calcular uma raiz.

8. E se o resultado da
divisão não for exato?
Só sai da raiz se o resultado for exato, caso
contrário, continua lá dentro.
Exemplos:


5.55125 23
==
5 2875 240355 4235
. ccbccbcb ==

9. E se o índice for
maior que o expoente
do radicando?
Podemos apenas dividir pelo mesmo número,
mas sem tirar de dentro da raiz.
Exemplos:


3 29 6
7,17,1 =
( ) ( )315 5
11 +=+ aa

10. Tente fazer sozinho
Simplifique o radical:
6 6123
8 zyx

11. Solução
xzyxzy
zyxzyx
22
28
26 332
6 612336 6123
=
==

12. Como indicamos uma raiz
sem usar o radical?
Trocando o índice e o expoente do radicando
por um expoente fracionário.
Exemplos:


( ) 3
53 5
22 =
( ) 2
1
2323 =
O expoente do
radicando vira
numerador e o
índice vira
denominador.

13. O que são radicais
semelhantes?
São os radicais que apresentam o mesmo
índice e o mesmo radicando.
Exemplo:
44
2725 e são semelhantes
2325 e são semelhantes
4
2525 e não são semelhantes
33
129e não são semelhantes

14. Como somamos e
subtraímos radicais?
Basta somar ou subtrair a quantidade de radicais
semelhantes.
Exemplo:
Caso fosse nada
poderíamos fazer, pois os radicais não são
semelhantes.
7276773 −=−+
76523 −+

15. Como multiplicamos
e dividimos radicais
de mesmo índice?
Basta juntar os radicandos dentro de um radical.
Exemplo:
55555
22
3
11.6
3:11.6 ==

16. E se os índices forem
diferentes?
Basta igualar os índices e juntar os radicandos.
Como igualamos os índices?
Basta achar o mmc entre os índices e ajustar os
expoentes dos radicandos.
Exemplo:
mmc (3,4) =12. Assim, temos:
Juntando no mesmo radical, temos:
43 2
7.5
12 312 8
7.5
12 38
7.5

17. Tente fazer
sozinho
(Vunesp) O valor da expressão
é igual a:
a) 2-1
b) 20
c) 21/2
d) 24
e) 26
2
4
3
1
4
3
8
2
:
8
16

18. Solução
( )
( )
4
4
63
6
44 12
6
44 34
23
4
3
4 3
2
4
3
1
4
3
2
2
2
2
2
2
2
:
2
2
2
2
:
2
2
2
2
:
8
16
8
2
:
8
16
=⋅=
===

19. Como elevamos um
radical a uma
potência?
Basta elevar o radicando a essa potência.
Exemplos:


( ) 44 33
4
2733 ==
( ) 12585852 33
==

20. Como extraímos a
raiz de um
radical?
Basta multiplicar os índices.
Exemplos:


6323
555 == x
242344 3
666 == xx

21. Tente fazer sozinho
Sabendo que e ,
calcule .
2=a 4
2=b
3
ab

22. Solução
== 3 43
22ab
mmc (2,4) = 4.
Logo, igualando os índices, temos:
123 43 43 44 2
882.422 ===

23. O que é
racionalização?
É o cálculo que usamos para tirar um
radical do denominador de uma fração.
Como racionalizamos um denominador?
Existem 3 procedimentos, que serão
descritos a seguir.

24. 1º) Quando o denominador é um produto e o
índice do radical é 2.
Basta multiplicar o numerador e o denominador
por .
Exemplos:


2
2
25
2.2
2.5
2
5
==
8
23
2.4
23
2.24
2.3
24
3
===

25. 2º) Quando o denominador é um produto
e o índice do radical é diferente 2.
Basta multiplicar o numerador e o denominador
pelo fator racionalizante.
O que é o fator racionalizante?
É o radical mais conveniente para eliminar o radical
do denominador.
Veja:
777.7 3 33 23
==
333.3 5 55 35 2
==
Fatores racionalizantes

26. Exemplo:
Tente fazer sozinho
Indique o valor da expressão:
7 3
7 3
7 7
7 3
7 37 4
7 3
7 4
36
3
3.18
3
3.18
3.3
3.18
3
18
====
3
6
5
3
1
4
3
2435
−++

27. Solução
3
6
36
6
35323336
6
35
3
3
2
3
3
6
35
3
3
2
3
3
6
35
3
1
4
3
3
3
6
5
3
1
4
3
243
10 55 5
5
==
=
−++
=−++
=−++=−++
=−++

28. 3º) O denominador é uma soma ou subtração.
Basta multiplicar numerador e denominador pelo
conjugado.
Veja: é conjugado de .
é conjugado de .
Exemplo:
32 − 32 +
57 + 57 −
( )
( )
( ) ( )
2
37
4
372
37
372
37.37
37.2
37
2
+
=
+
=
−
+
=
+−
+
=
−

29. Tente fazer
sozinho
(UFSE) Racionalizando-se o denominador de
obtém-se:
52
3
+

30. Solução
( )
( )( )
( ) ( ) 52
3
52.3
52
52.3
5252
52.3
52
3
+−=
−
+
=
−
+
=
++
+
=
+