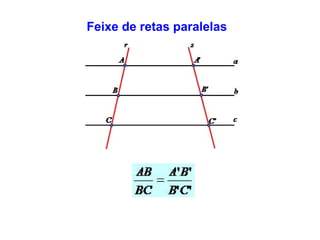
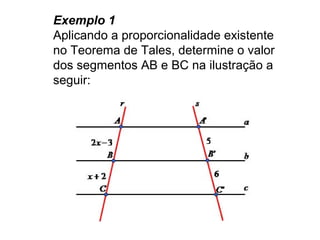
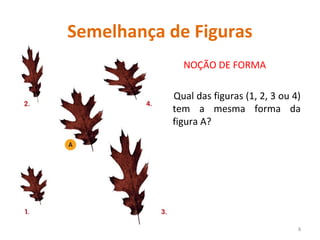
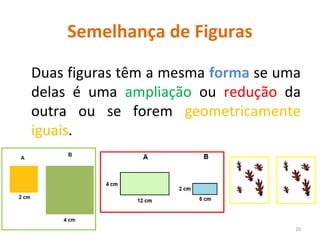
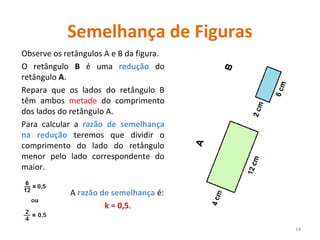
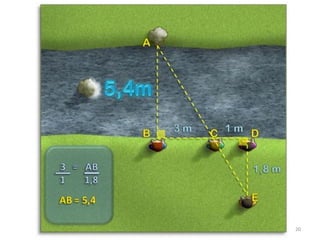
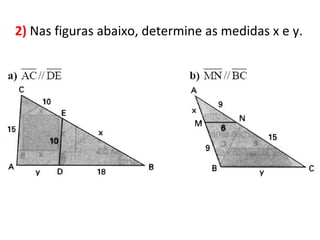
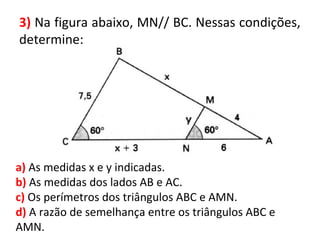
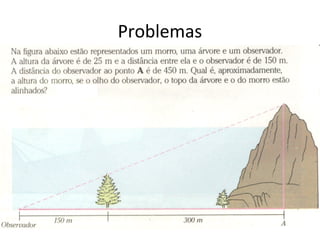
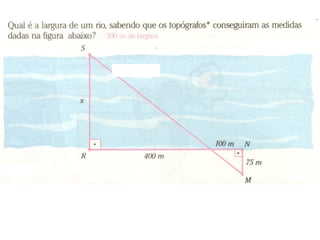
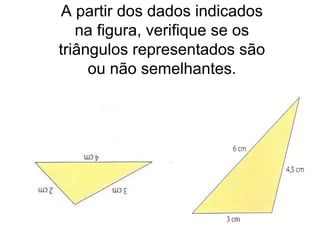
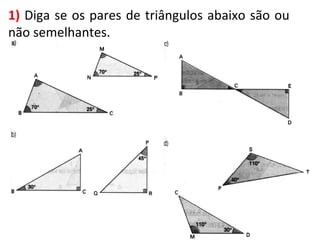
1. O documento discute o Teorema de Tales e a semelhança de figuras geométricas. 2. Explica que duas figuras são semelhantes se tiverem a mesma forma, ou seja, se uma for uma ampliação ou redução da outra. 3. Detalha as condições para que polígonos sejam considerados semelhantes, incluindo ângulos correspondentes congruentes e lados correspondentes proporcionais.

1. 1
Teorema de Tales
e Semelhança

2. Teorema de Tales
Tales de Mileto viveu Na Grécia
por volta dos anos 600 antes de
Cristo.
Em muitas de suas viagens, diz a
lenda, foi desafiado a calcular a
altura de uma pirâmide, no Egito.

3. 3

4. Feixe de retas paralelas

6. Exemplo 1
Aplicando a proporcionalidade existente
no Teorema de Tales, determine o valor
dos segmentos AB e BC na ilustração a
seguir:

7. Semelhança
de
Figuras
7

8. Semelhança de Figuras
NOÇÃO DE FORMA
Qual das figuras (1, 2, 3 ou 4)
tem a mesma forma da
figura A?
8

9. Semelhança de Figuras
Devem ter reparado que apenas a figura 1 tem a
mesma forma da figura A.
Isso só acontece porque:
a figura 1 é uma redução da figura A
ou
a figura A é uma ampliação da figura 1.
9

10. Semelhança de Figuras
10
Duas figuras têm a mesma forma se uma
delas é uma ampliação ou redução da
outra ou se forem geometricamente
iguais.

11. Semelhança de Figuras
Conclusão:
Duas figuras são semelhantes se
tiverem a mesma forma.
As 3 figuras são semelhantes.
F1 e F3 são geometricamente
iguais e F2 é uma ampliação das
outras.
Para dizer que as figuras são
semelhantes escreve-se:
F1 ~ F2 ~ F3
11

12. Semelhança de Figuras
Os dois quadrados representados ao lado
são semelhantes.
12
Repare que o quadrado B é uma
ampliação do quadrado A.
Se dividirmos o comprimento do lado do
quadrado B pelo comprimento do lado do
quadrado A, teremos:
A medida dos lados do quadrado B é o
dobro da medida dos lados do quadrado
A.
O número 2 é a razão de semelhança na
ampliação.

13. Semelhança de Figuras
Para representar a razão de semelhança usa-se a letra k.
Para o caso anterior, podemos dizer que a razão de semelhança na
ampliação do quadrado A para o quadrado B é:
k = 2
Pode ainda dizer-se que o quadrado
B é uma ampliação do quadrado A
na escala 2:1.
13

14. Semelhança de Figuras
Observe os retângulos A e B da figura.
O retângulo B é uma redução do
retângulo A.
Repara que os lados do retângulo B
têm ambos metade do comprimento
dos lados do retângulo A.
Para calcular a razão de semelhança
na redução teremos que dividir o
comprimento do lado do retângulo
menor pelo lado correspondente do
maior.
A razão de semelhança é:
k = 0,5.
14

15. Semelhança de Figuras
Se as duas figuras forem geometricamente iguais, qual será a
razão de semelhança de uma para a outra?
Repare que, sendo as figuras geometricamente iguais, elas
têm as mesmas dimensões.
Neste caso, a razão de semelhança é 1 (ou seja, k = 1).
15

16. Semelhança de Figuras
CONDIÇÃO: Dois ou mais polígonos são ditos
semelhantes
quando:
- Os ângulos correspondentes são congruentes;
- As medidas de lados correspondentes são
proporcionais.
- Neste caso é necessário satisfazer as duas condições.
16

17. Semelhança de Figuras
Numa redução a razão de semelhança é menor do
que 1 (k < 1).
Numa ampliação a razão de semelhança é maior do
que 1 (k > 1).
Entre duas figuras geometricamente iguais a razão
de semelhança é igual a 1 (k = 1).
17

18. Semelhança de Polígonos
CONDIÇÃO: Dois ou mais polígonos são ditos
Semelhantes quando:
- Os ângulos correspondentes são congruentes;
- As medidas de lados correspondentes são
proporcionais.
- Neste caso é necessário satisfazer as duas condições.
18

19. 1º CASO: AA (Ângulo,Ângulo)
Dois triângulos semelhantes tem os
mesmos ângulos.
Os lados correspondentes são
proporcionais.

20. 20

21. 2º Caso: LLL (Lado, Lado, Lado)
Dois triângulos são semelhantes se os
lados de um são proporcionais aos lados
do outro

22. A partir dos dados indicados
na figura, verifique se os
triângulos representados são
ou não semelhantes.

23. 3º Caso: LAL
Dois triângulos são semelhantes se os
lados de um são proporcionais aos lados
do outro e se o ângulo por eles
compreendido tem a mesma medida.

24. Observação
Com base nos casos de semelhança estudados,
podemos ter os seguintes resultado:
Se a razão de semelhança de dois triângulos
semelhantes é k, então:
A razão entre os lados correspondentes é k;
A razão entre as alturas correspondentes é k;
A razão entre os perímetros é k;

25. 1) Diga se os pares de triângulos abaixo são ou
não semelhantes.

26. 2) Nas figuras abaixo, determine as medidas x e y.

27. 3) Na figura abaixo, MN// BC. Nessas condições,
determine:
a) As medidas x e y indicadas.
b) As medidas dos lados AB e AC.
c) Os perímetros dos triângulos ABC e AMN.
d) A razão de semelhança entre os triângulos ABC e
AMN.

28. Problemas