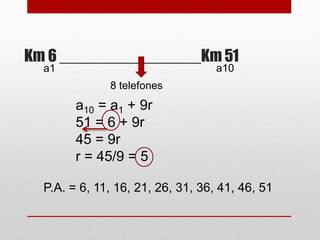
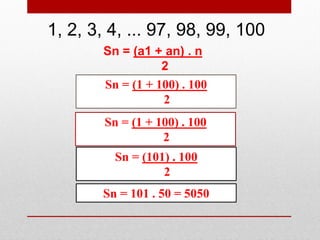
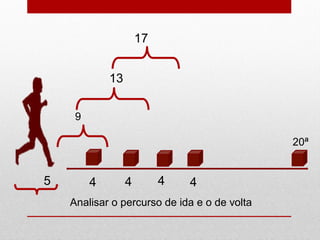
O documento discute progressão aritmética, definindo-a como uma sequência na qual cada termo subsequente é igual ao anterior somado a uma constante chamada razão. Exemplos de cálculo do termo geral e resolução de problemas envolvendo distâncias percorridas em progressão aritmética são apresentados.

1. PROGRESSÃO
ARITMÉTICA
Professora: Rosânia

2. EXISTEM VÁRIOS TIPOS DE SUCESSÕES E
SEQUÊNCIAS
• O ALFABETO
• AS VOGAIS
• SEQUENCIAS NUMÉRICAS
2, 10, 12, 16, 18, 19
QUAL É O PROXIMO NÚMERO DA
SEQUENCIA?
2, 10, 12, 16, 18, 19, ....

3. O PROXIMO NÚMERO
DA
SEQUENCIA?
2, 10, 12, 16, 18, 19, ....
200
COMEÇA COM A LETRA D.
NÃO É PROGRESSÃO ARITMÉTICA

4. PROGRESSÃO ARITMÉTICA
•É uma sequência na qual cada
termo, a partir do segundo, é
igual ao termo anterior somado
a uma constante chamada
RAZÃO.

5. PROGRESSÃO ARITMÉTICA
 EX: 2, 4, 6, 8, 10, 12, 14 ,16
1º TERMO = 2
2º TERMO = 4
3º TERMO = 6
......
VARIAÇÃO DE 2 EM 2 - CHAMADA DE
RAZÃO DA SEQUÊNCIA

6. CLASSIFICAÇÃO
 P.A. crescente, onde a razão é um número
positivo, maior que zero
2, 4, 6, 8, 10, 12, 14, 16 R = 2 > 0
 P.A. decrescente, onde a razão é um número
negativo ( no caso – 5)
10, 5, 0, -5, -10 R = -5 < 0
 P.A. constante, onde a razão é zero
5, 5, 5, 5, 5, 5... R = 0

7. PROGRESSÃO ARITMÉTICA
a1 é o primeiro termo da P.A.
a2 é o segundo termo da P.A.
a3 é o terceiro termo da P.A.
an é o último termo da P.A.
r é a razão da P.A.
n é o número de termo da P.A.
A P.A. pode ser finita ou infinita

8. Considere uma P.A finita qualquer (a1, a2,
a3, a4, ... , an) de razão igual a r, sabemos
que:
a2 = a1 + r
a3 = a1 + 2r
a4 = a1 + 3r
…
an = a1 + (n – 1) . r
TERMO GERAL DE UMA P.A

9. Ex: Calcule o 16º termo de uma
P.A, sabendo que a1 = -10 e r = 3.
an = a1 + (n – 1) . r ou a16 = a1 + 15r
a16 = -10 + (16 – 1) . 3
a16 = -10 + 15 . 3
a16 = -10 + 45
a16 = 35
O 16º termo de uma P.A é 35.

10. PROBLEMA:
Uma pessoa pretendendo melhorar seu
condicionamento físico inicia um sistema de
corridas diárias com um aumento de 400m por
semana no seu trajeto.
Na primeira semana foram completados 2 km.
Qual a distância percorrida na décima semana?

11. Uma pessoa pretendendo melhorar seu condicionamento físico inicia
um sistema de corridas diárias com um aumento de 400m por
semana no seu trajeto.
Na primeira semana foram completados 2 km.
Qual a distância percorrida na décima semana?
A10 = a1 + 9r
A10 = 2km + 9 . 400m
A10 = 2km + 3600m
A10 = 2000m + 3600m
A10 = 5 600m ou 5,6 km
SOLUÇÃO:

12. SIGNIFICADO DE INTERPOLAÇÃO
Ex: Numa estrada existem dois telefones
instalados no acostamento: um no km 6 e
outro no km 51. Entre eles serão colocados
mais 8 telefones. Mantendo-se entre dois
telefones consecutivos a mesma distância.
Determine em quais marcas quilométricas
deverão ficar esses telefones.

13. Km 6 ________________Km 51
8 telefones
a1 a10
a10 = a1 + 9r
51 = 6 + 9r
45 = 9r
r = 45/9 = 5
P.A. = 6, 11, 16, 21, 26, 31, 36, 41, 46, 51

14. SOMA DOS TERMOS DE UMA P.A
Faça a soma desses termos de forma algébrica.
2+5+8+11+14+17+20+23 = 100
S8 = 100

15. SOMA DOS TERMOS DE UMA P. A
1, 2, 3, 4, ... 97, 98, 99, 100
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
4 + 97 = 101
a1 + a100 = 101
a2 + a99 = 101
Dos cem números FORMARAM-SE 50 pares
O resultado da soma de cada dois pares dá 101,
então:
101 x 50 = 5050

16. SOMA DOS TERMOS DE UMA P. A
Sn = (a1 + an) . n
2
Sn = soma dos n termos
a1 = é o primeiro termo
an = é o último termo
n = é o número de termos

17. 1, 2, 3, 4, ... 97, 98, 99, 100
Sn = (a1 + an) . n
2
Sn = (1 + 100) . 100
2
Sn = (1 + 100) . 100
2
Sn = (101) . 100
2
Sn = 101 . 50 = 5050

18. EX: Em uma gincana, 20 caixinhas estão distribuídas ao
longo de uma pista retilínea, distantes 4m uma da outra.
Um competidor que se encontra a 5m da primeira
caixinha, deve correr até a primeira caixinha, pegar um
objeto e retornar ao ponto de partida. Em seguida ele vai
até a segunda caixinha retira um objeto e retorna ao
ponto de partida, e assim sucessivamente, até atingir a
vigésima caixinha. Quantos metros esse competidor
deverá percorrer para realizar a prova?

19. 5 4 4 4
9
13
17
20ª
Analisar o percurso de ida e o de volta
4

20. Antes deve-se achar o vigésimo termo:
an = a1 + (n – 1) . r
a20 = a1 + 19 . r
a20 = 5 + 19 . 4
a20 = 5 + 76
a20 = 81 Último termo

21. s20 = (a1 + a20) . 20
2
Sn = (a1 + an) . n
2
s20 = (5 + 81) . 20
2
s20 = 86 . 20 = 1720 = 860m
2 2
Caminho de ida e volta multiplica por 2
860 x 2 = 1720 m

22. FÓRMULA DA RAZÃO
a2 – a1 = a3 – a2

23. Determine o valor de x, de modo que os números 3x -1, x+3 e
x+9 estejam, nessa ordem, e PA.
a1 a2
a3
x = ? a2 – a1 = a3 – a2
(x + 3) – (3x – 1) = (x + 9) – (x + 3)
x + 3 – 3x + 1 = x + 9 – x – 3
- 2x + 4 = 6
- 2x = 6 – 4
- 2x = 2
x = - 2/2
x = -1

24. PROPRIEDADE IMPORTANTE:
PA com três termos CONHECIDOS
Cada termo é igual à média aritmética dos
seus equidistantes

25. Aplicando a propriedade: o termo do meio é a
média dos vizinhos. (soma e divide por 2)

26. PROVA REAL DA QUESTÃO ANTERIOR
Substitui o valor encontrado no x da questão.
x + 5, 5x – 7, 4x + 1
9 13 17
Descubra qual o próximo termo.

27. PA com três termos DESCONHECIDOS

28. Ex: Achar a razão da PA (x, 2x + 5, 32).
Nesse caso, utilizaremos a propriedade da média
aritmética para resolver o problema.
Assim, sabemos que .
Resolvendo a equação, temos:

29. Logo, a PA é .
E sua razão é .