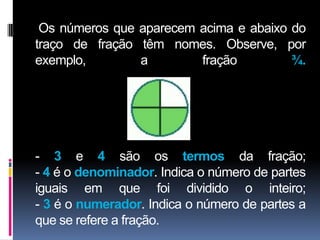
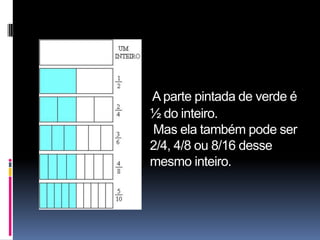
1) O documento apresenta o estudo histórico e conceitual sobre frações, desde seu uso no Egito Antigo até sua definição matemática. 2) Aborda os significados e leituras de diferentes frações como 1/2, 1/3 e 4/6, além de explicar os termos numerador e denominador. 3) Discorre sobre tipos de frações como próprias, impróprias e aparentes e o conceito de equivalência entre frações.

1. O Estudo das Frações
FERNANDA CRISTINA BORGATTO
LANTE – LABORATÓRIO DE NOVAS
TECNOLOGIAS DE ENSINO DA MATEMÁTICA
INFORMÁTICA EDUCATIVA II

2. Um pouco de história......
Os documentos mais antigos que registram o
uso de frações têm origem no Egito antigo.
Naquele período, os egípcios viviam à beira do
rio Nilo, nas terras que pertenciam ao faraó. O
povo pagava ao faraó impostos proporcionais à
área que ocupava.
De tempos em tempos, o rio Nilo transbordava,
as demarcações das terras feitas pelos
agricultores desapareciam, e novas marcações
precisavam ser feitas. Elas eram realizadas
com pedaços de cordas, marcadas com nós
igualmente espaçados.

3. Mas se o pedaço de corda entre dois nós
não cabia um número exato de vezes npo
comprimento a ser medido... Temos de
dividir novamente este pedaço!
Em muitas situações, a unidade escolhida
não cabia um números exato de vezes no
comprimento que estava sendo medido. A
solução foi dividi-la em partes iguais e usar
uma ou mais das partes dessa unidade.
Assim foram criadas as FRAÇÕES.

4. Mas qual os significados de
fração?
Usamos frações para representar números
que indicam uma ou várias partes de um
todo que foi dividido em partes iguais.
Esse todo a que se refere uma fração será
chamado de inteiro. Um inteiro pode ser,
entre outras coisas, um pedaço de corda,
um pedaço de terra, um grupo de pessoas,
uma coleção de objetos.

5. Veja algumas frações e seus significados:
Significado da fração 1/2 (um meio)
1/2
1/2
1/2
½ da figura é a metade desta figura, da mesma
forma que ½ de um pedaço de corda por
exemplo é a metade do pedaço de corda e ½ de
12 bolas é a metade do número total de bolas
ou seja 6 bolas.

6. Quando um inteiro é dividido em duas partes
iguais, cada parte pode ser representada pela
fração ½.

7. Significado da fração 1/3 (um terço)
3/3
1/3
1/3
1/3
1/3 da figura , é a terça parte dessa figura, ou
seja a figura é dividida em 3 parte iguais onde
cada uma dessas partes representa 1/3, da
mesma forma que 1/3 de um pedaço de corda é
a terça parte do pedaço todo, 1/3 de 12 bolas é
a terça parte de 12, ou seja 4 bolas.

8. Quando um inteiro é dividido em três partes
iguais, cada parte pode ser representada pela
fração 1/3.

9. Significado da fração 4/6 (quatro sexto)
4/6
1/6 1/6 1/6
1/6 1/6 1/6
4/6 da figura correspondem a 4 pedaços iguais
a 1/6, ou 4/6 de um pedaço de corda
correspondem a 4 pedaços iguais a 1/6 desta
corda, ou 4/6 de 12 bolas correspondem 8
bolas.

10. Quando um inteiro é dividido em seis partes
iguais, quatro dessas partes podem ser
representadas pela fração 4/6.

11. Os números que aparecem acima e abaixo do
traço de fração têm nomes. Observe, por
exemplo, a fração ¾.
- 3 e 4 são os termos da fração;
- 4 é o denominador. Indica o número de partes
iguais em que foi dividido o inteiro;
- 3 é o numerador. Indica o número de partes a
que se refere a fração.

12. Leitura de frações
A leitura de uma fração depende do seu
denominador.
Quando o denominador de uma fração é 10,100
ou 1000, lê-se o numerador e acrescenta-se a
palavra décimo, centésimo ou
milésimo, respectivamente.
3/10 – lê-se três décimos
15/100 – lê-se quinze centésimos
7/1000 – lê-se sete milésimos

13. Quando o denominador de uma fração é menor
do que 10, existe uma palavra para a leitura de
cada fração, de acordo com o denominador:
½ - um meio ou meio
2/3 – dois terços
¾ - três quartos
2/5 – dois quintos
1/6 – um sexto
4/7 – quatro sétimos
6/8 – seis oitavos
5/9 – cinco nonos

14. Quando o denominador é maior que 10, lê-se o
numerador, o denominador e acrescenta-se a
palavra avos:
6/21 – seis vinte e um avos
5/2000 – cinco dois mil avos

15. A utilização do conceito de fração
na resolução de problemas:
- Para fazer um bolo de casamento, Dona
Joana precisa de 3/5 dos ovos
que estão nesta bandeja.
Quantos ovos ela usará para
fazer o bolo?
Primeiro calculamos 1/5 de 30
ovos, em seguida, 3/5 de 30 ovos.
3/5 de 30 correspondem a 3 grupos de 1/5.
1/5 de 30 é o mesmo que 30:5=6, ou seja, 1/5
de 30 é igual a 6.

16. 3/5 de 30 é o mesmo que 3 vezes 1/5 de 30, ou
seja, 3/5 de 30 é igual a 3x6=18
Logo, Joana usará 18 ovos.

17. Tipos de fração
Na fração 7/10, o numerador 7 é menor que o
denominador 10. Dizemos que 7/10 é uma fração
própria.
As frações próprias têm numerador menor que
o denominador.
Na fração 13/10, como 13 é maior do que 10,
dizemos que 13/10 é uma fração imprópria.
Nas frações impróprias, o numerador é maior
que o denominador.
Existem frações onde o numerador é múltiplo do
denominador.

18. Frações deste tipo são chamadas frações
aparentes. Veja alguns exemplos:
18/3 – é múltiplo de 3
18/3 – é uma fração aparente igual a 6.
Observe: 18/3=18:3=6
500/4 – 500 é múltiplo de 4.
500/4 – é uma fração aparente igual a 125.
Observe: 500/4=500:4=125

19. Equivalência de Frações
Existem frações que têm numeradores e
denominadores diferentes, mas que podem
representar a mesma parte de um mesmo
inteiro. Vamos ver como isso acontece?
Observe o desenho a seguir no qual as tiras
retangulares são todas iguais: a primeira delas
representa o inteiro, e as demais estão divididas
em partes iguais.

20. A parte pintada de verde é
½ do inteiro.
Mas ela também pode ser
2/4, 4/8 ou 8/16 desse
mesmo inteiro.

21. - Quando se divide um inteiro em 2 partes
iguais, 1 parte corresponde a ½ do inteiro.
Dividindo o mesmo inteiro em 4 partes iguais,
quantas partes corresponderão a ½ do inteiro?
Nessa situação, que fração representa ½?
- E quando se divide o mesmo inteiro em 10
partes iguais, quantas partes corresponderão a
½ do inteiro? Nessa situação, que fração
representa ½?

22. Resposta da primeira pergunta:
R: 2 partes; 2/4;
Resposta da segunda pergunta:
R: 5 partes; 5/10.

23. As frações ½; 2/4; 3/6; 4/8 e 5/10 representam a
mesma parte da tira retangular, que é o inteiro.
Em Matemática dizemos que elas são frações
equivalentes, mas é comum dizer que são
frações iguais. Assim, escrevemos:
½=2/4=3/6=4/8=5/10
Além dessa, existem outras frações equivalentes
a ½:
½=16/32=50/100=460/920=....