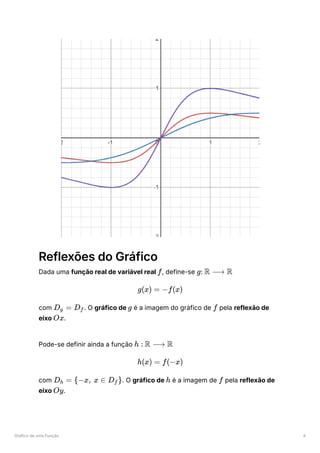
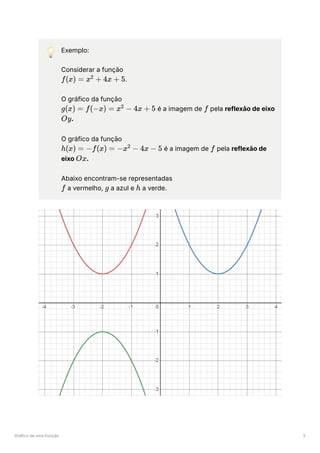
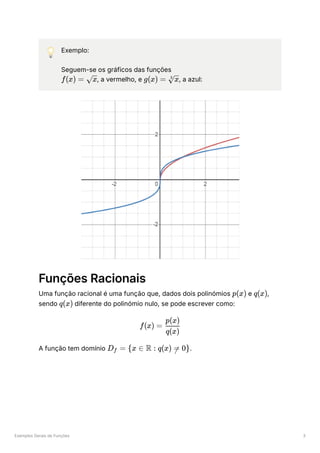
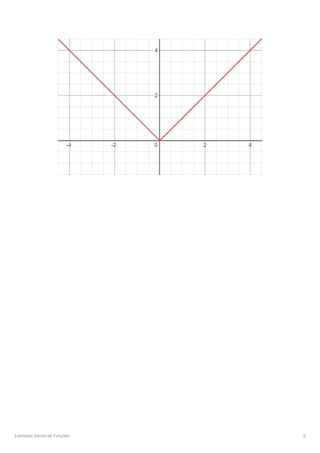
O documento aborda conceitos fundamentais sobre funções reais de variável real, incluindo definições de domínio, contradomínio, e tipos de funções como injetivas, sobrejetivas, e bijetivas. Também são discutidas operações com funções, a composição de funções, a noção de função inversa, e as propriedades de funções como paridade e limites. Além disso, o documento explora gráficos de funções e transformações gráficas, incluindo translações, dilatações e reflexões.

![Generalidades acerca de Funções 2
é o conjunto dos números reais para os quais está bem
definido.
Função Injetiva, Sobrejetiva e Bijetiva
Uma função diz-se injetiva se e só se:
Ou, de forma equivalente:
💡 Exemplo:
A função
é injetiva, já que resulta da soma de duas funções
injetivas: e
.
A função
não é injetiva, já que
, por
exemplo, e
.
Uma função diz-se sobrejetiva se e só se:
Por outras palavras, o contradomínio de f (tipicamente representado por
)
coincide com o seu conjunto de chegada (o contradomínio de uma função é o
conjunto dos pontos no conjunto de chegada que são a imagem de um
elemento do domínio).
D =
f×g D ∩
f D
g
( )(x) =
g
f
g(x)
f(x)
D =
g
f D ∩
f {x ∈ D :
g g(x) =
0}
f (x) =
r
[f(x)] , r ∈
r
Q
D
fr x [f(x)]r
f : A → B
∀
:
x,y ∈ A f(x) = f(y) ⟹ x = y
∀ :
x,y ∈ A x =
y ⟹ f(x) =
f(y)
f(x) = x +
3
3x
f
(x) =
1 x3
f
(x) =
2 3x
g(x) = x2
∃ :
x,y∈D
f
x =
y ∧ f(x) = f(y)
x = 1 y = −1
f : A → B
∀ ∃ :
y ∈ B x ∈ A y = f(x)
D
f
′](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-2-320.jpg)





![Generalidades acerca de Funções 8
💡 Exemplo:
A função
não tem máximo nem mínimo absolutos, já que não é
limitada. Tem um máximo relativo para e um mínimo relativo
para
.
é crescente em e em
; é decrescente em
.
f(x) = x +
3
x2
x = −
2
3
x = 0
f ] − ∞;−
]
2
3
[0;+∞[ f
[− ;0]
2
3](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-8-320.jpg)














![Condições e Conjuntos 4
A negação de uma condição universal é uma condição
impossível e vice-versa.
Dada uma condição p(x) e um conjunto U:
Conjuntos e condições
Igualdade de conjuntos
Dados dois conjuntos A e B, A=B se e somente se:
Condições equivalentes
Duas condições são equivalentes num conjunto se e somente se definem o
mesmo conjunto em
Interseção de Conjuntos
Dados dois conjuntos A e B, chama-se interseção de A com B (
) ao
conjunto:
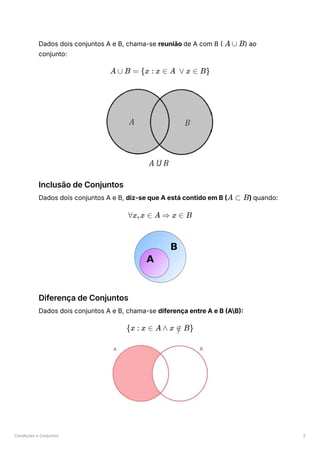
Reunião de Conjuntos
∼ [∀x ∈ U,p(x)] ⇔ ∃x ∈ U :∼ p(x)
∼ [∃x ∈ U : p(x)] ⇔ ∀x ∈ U, ∼ p(x)
∀x,x ∈ A ⇔ x ∈ B
U
U.
A ∩ B
A ∩ B = {x : x ∈ A ∧ x ∈ B}](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-28-320.jpg)
![Condições e Conjuntos 6
Dados dois conjuntos A e B, A=B se e somente se e
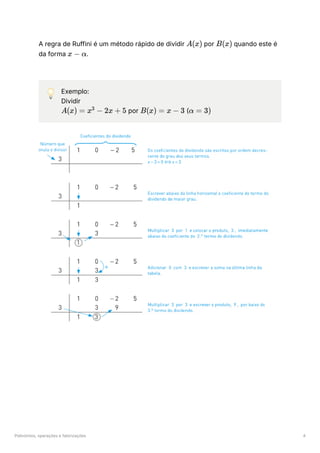
Implicação entre Condições
Dupla Implicação
Contrarrecíproca
A ⊂ B
B ⊂ A
[∀x,p(x) ⇔ q(x)] ⇔ ∀x,(p(x) ⇒ q(x)) ∧ (q(x) ⇒ p(x))
∀x,(p(x) ⇒ q(x)) ⇔ ∀x,(∼ q(x) ⇒∼ p(x))](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-30-320.jpg)












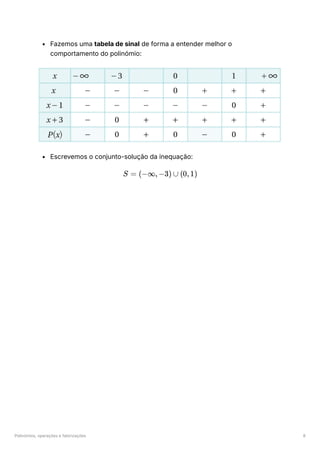





![Distâncias no Plano 2
Dado um segmento de reta de
a
,
, o seu ponto médio
M é o ponto equidistante dos seus extremos, e é obtido pela expressão:(falta
meter imagem)
💡 Exemplo:
Determinar M, o ponto médio entre A(2,6) e B(8,-2).
Mediatriz de um segmento de reta
Dado um segmento de reta de
a
, a sua mediatriz é a reta
perpendicular ao segmento que passa pelo ponto M( ponto médio de
).
Qualquer ponto da mediatriz é equidistante aos extremos do segmento de reta
correspondente, neste caso aos pontos A e B.
A(a
,a
)
1 2 B(b
,b
)
1 2 [AB]
M = ( , )
2
a + b
1 1
2
a + b
2 2
M = (
,
) =
2
2 + 8
2
6 + (−2)
(5,2)
A(a
,a
)
1 2 B(b
,b
)
1 2
[AB]](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-50-320.jpg)
![Distâncias no Plano 3
A sua expressão pode ser encontrada pela fórmula:
💡 Exemplo:
Dado o segmento de reta [AB], com A(1,5) e B(4,7), determine a
equação da sua mediatriz:
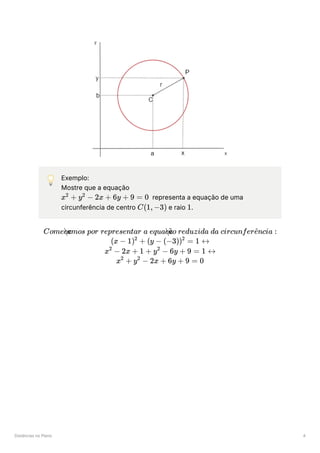
Equação reduzida da circunferência
Sendo o centro de uma circunferência de raio r, o ponto
pertence só pode pertencer à sua circunferência se a
. Assim
conseguimos obter a sua expressão reduzida:
(x − a
) +
1
2
(y − a
) =
2
2
(x − b
) +
1
2
(y − b
)
2
2
(x − 1) +
2
(y − 5) =
2
(x − 4) +
2
(y − 7) ↔
2
x −
2
2x + 1 + y −
2
10y + 25 = x −
2
8x + 16 + y −
2
14y + 49 ↔
4y = −6x + 39 ↔ y = − x +
2
3
4
39
C(x
,y
)
1 1 P(x,y)
d(C,P) = r
(x − x
) +
1
2
(y − y
) =
1
2
r2](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-51-320.jpg)
![Vetores e Coordenadas 1
Vetores e Coordenadas
Segmentos orientados, vetores e a sua
norma
Segmentos orientados equipolentes
Dois segmentos orientados são equipolentes quando têm a mesma direção,
sentido e comprimento.
💡 Exemplo:
Dado um paralelogramo [ABCD] os segmentos [A,D] e [B,C] são
segmentos orientados equipolentes.
Vetor
Um vetor é caraterizado por uma direção, um sentido e um comprimento, e
podem ser:
Colineares: Se tiverem a mesma direção;
Simétricos: Se tiverem a mesma direção, comprimento e sentidos opostos
v](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-53-320.jpg)









![Distâncias e Conjuntos no Espaço 2
Retas paralelas aos eixos coordenados
Já as retas paralelas aos eixos coordenados terão 2 coordenadas previamente definidas.
Podem ser paralelas ao eixo:
, a reta terá como vetor diretor e equação:
, a reta terá como vetor diretor e equação:
Z, a reta terá como vetor diretor e equação:
Distância entre 2 pontos no espaço
A distância entre 2 pontos e no espaço é calculada como no plano,
apenas com a adição da terceira coordenada:
💡 Exemplo:
Encontra a distância entre o ponto A(1,4,8) e o ponto B(-1,7,1).
Plano mediador de um segmento de reta
O plano mediador do segmento de reta
(pontos
) pode ser calculado
da mesma forma que a mediatriz, mais uma vez adicionando a terceira coordenada:
Todos os pontos contidos no plano mediador são equidistantes a e
.
X (1,0,0)
v
y = a ∧ z = b
Y (0,1,0)
v
x = a ∧ z = b
(0,0,1)
v
x = a ∧ y = b
P
(x
,y
,z
)
1 1 1 1 P
(x
,y
,z
)
2 2 2 2
d(P
,P
) =
1 2
(x
− x
) + (y
− y
) + (z
− z
)
2 1
2
2 1
2
2 1
2
d(A,B) = =
(−1 − 1) + (7 − 4) + (1 − 8)
2 2 2
62
[AB] A(a
,a
,a
)eB(b
,b
,b
)
1 2 3 1 2 3
(x − a
) +
1
2
(y − a
) +
2
2
(z − a
) =
3
2
(x − b
) +
1
2
(y − b
) +
2
2
(z − b
)
3
2
A B](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-63-320.jpg)
![Distâncias e Conjuntos no Espaço 3
💡 Exemplo:
Dado o segmento de reta [AB], com A(1,5,3) e B(4,7,2), determine a equação do plano
mediador:
Superfície esférica e esfera
Mais uma vez podemos relacionar a superfície esférica com o seu equivalente no plano, a
circunferência. A esfera conterá também o interior da superfície esférica(assim como o círculo no
plano continha o interior da circunferência).
As suas equações reduzidas são dadas por:
Superfície Esférica:
Esfera:
💡 Exemplo:
Determine a equação de uma superfície esférica de centro
e raio
.
(x − 1) +
2
(y − 5) +
2
(z − 3) =
2
(x − 4) +
2
(y − 7) +
2
(z − 2) ↔
2
x −
2
2x + 1 + y −
2
10y + 25 + z −
2
6z + 9 = x −
2
8x + 16 + y −
2
14y + 49 + z −
2
4z + 4 ↔
4y + 6x − 2z = 32
(x − x
) +
1
2
(y − y
) +
1
2
(z − z
) =
1
2
r2
(x − x
) +
1
2
(y − y
) +
1
2
(z − z
) ≤
1
2
r2
C(1,−3,2) 1
Come
amos por representar a equa o reduzida da superf cie esf rica :
c
c c
c
a
~ ı
ˊ e
ˊ
(x − 1) +
2
(y − (−3)) +
2
(z − 2) =
2
1 ↔
x −
2
2x + 1 + y −
2
6y + 9 + z −
2
4z + 4 = 1 ↔
x +
2
y +
2
z −
2
2x + 6y − 4z + 13 = 0](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-64-320.jpg)





![Vetores no Espaço e Produto Escalar 5
Circunferência e Superfície Esférica
Sejam 2 pontos A e B, a circunferência ou respetiva superfície esférica de
diâmetro pode ser obtida pela expressão:
💡 Exemplo:
Encontrar a circunferência de diâmetro [AB] sendo A(1,2) e B(-1,0):
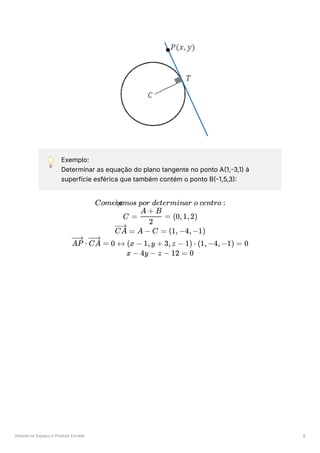
Reta ou plano tangente a uma circunferência ou superfície
esférica
Dados uma circunferência ou superfície esférica de centro C que contém o
ponto T, a reta ou(respetivamente) o plano tangente no ponto T é dado por:
M = =
2
A + B
(
,
,
) =
2
1 − 1
2
0 + 2
2
4 + 8
(0,1,6)
=
AB B − A = (−2,−2,4)
=
MP P − M = (x,y,z) − (0,1,6) = (x,y − 1,z − 6)
⋅
MP =
AB 0 ↔ (x,y − 1,z − 6) ⋅ (−2,−2,4) ↔
−2x − 2y + 4z − 22 = 0 ↔ −x − y + 2z − 11 = 0
[AB]
⋅
AP =
BP 0
(x − 1,y − 2) ⋅ (x + 1,y) = 0
x +
2
y −
2
2y − 1 = 0
⋅
TP =
CT 0](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-70-320.jpg)


![Resolução de Triângulos 1
Resolução de Triângulos
Razões Trigonométricas de um Ângulo Agudo
Considere o triângulo retângulo em
:
Define-se:
💡 Exemplo:
Dado um triângulo retângulo, cuja hipotenusa mede
e no qual um dos ângulos internos seja de
→ O cateto adjacente a esse ângulo mede
→ O cateto oposto a esse ângulo mede
É de notar que o Teorema de Pitágoras se verifica:
[ABC] A
sin α =
BC
AB
cosα =
BC
AC
tan α =
AC
AB
2 m 30º :
2 ⋅ cos30º = 2 =
2
3
3
2 ⋅ sin 30º = 2 =
2
1
1
1 +
2
=
3
2
1 + 3 = 4 = 22](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-76-320.jpg)
![Resolução de Triângulos 2
Lei dos Senos
Para qualquer triângulo
:
💡 Exemplo:
Esta relação permite mostrar que um triângulo isósceles, que tem
dois lados iguais, também tem dois ângulos iguais. Suponhamos
lados
e com ângulos opostos, respetivamente, e
.
Suponhamos ainda
, ou seja, que o triângulo é isósceles.
Então, a lei dos senos lê:
Poderá parecer que o segundo caso nos provou errados: existe um
caso em que
. No entanto, recordemos que:
Ou seja, o triângulo em que
não existe. Logo, um triângulo isósceles tem sempre
dois ângulos iguais.
[ABC]
=
BC
sin(α)
=
CA
sin(β)
AB
sin(γ)
A,B C α,β γ
A = B
=
A
sin(α)
⟺
B
sin(β)
=
A
sin(α)
⟹
A
sin(β)
α = β ∨ α = 180º − β
α =
β
α + β + γ = 180º ⟺ 180º − β + β + γ = 180º ⟺ γ = 0
α = 180º − β](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-77-320.jpg)
![Resolução de Triângulos 3
Para qualquer triângulo
:
💡 Exemplo:
Suponhamos
e
. Podemos encontrar o comprimento em
função do ângulo
, através da lei dos cossenos! A fórmula fica:
Abaixo encontra-se um gráfico desta função para
. Repara que os valores mínimo e máximo são de e
,
respetivamente. Consegues explicar porquê?
[ABC]
=
BC
2
+
AC
2
−
AB
2
2 cosα
AC AB
=
AC
2
+
AB
2
−
BC
2
2 cosβ
AB BC
=
AB
2
+
AC
2
−
BC
2
2 cosγ
AC BC
=
AB 3 =
BC 2 AC
β
=
AC ⟺
9 + 4 − 2 ⋅ 3 ⋅ 2 cosβ =
AC
13 − 12 cosβ
β ∈]0,180º[ 1 5](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-78-320.jpg)
![Ângulos Generalizados, Fórmulas Trigonométricas 1
Ângulos Generalizados,
Fórmulas Trigonométricas
Ângulos Generalizados
Dado e
, define-se o ângulo generalizado como o par
ordenado que satisfaz:
se
se
α ∈ [−360º,360º] n ∈ N
(α,n)
n ≥ 0, α ∈ [0º,360º]
n ≤ 0, α ∈ [−360º,0º]](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-79-320.jpg)




![A Circunferência Trigonométrica 1
A Circunferência
Trigonométrica
A Circunferência Trigonométrica é um objeto matemático útil para o cálculo do
seno, cosseno e tangente de ângulos que não se encontram no intervalo
,
e define-se como o conjunto:
Seno
Dado um ângulo
, desenhar uma semirreta com inclinação
, que passe na
origem
[0, ]
2
π
S
=
1 {(x,y) ∈ R :
2
x +
2
y =
2
1}
θ θ](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-84-320.jpg)








![Equações e Inequações Trigonométricas 6
💡 Exemplo:
Voltemos duas equações acima, e modifiquemos ligeiramente a
expressão. Além disso, procuremos apenas soluções no intervalo
:
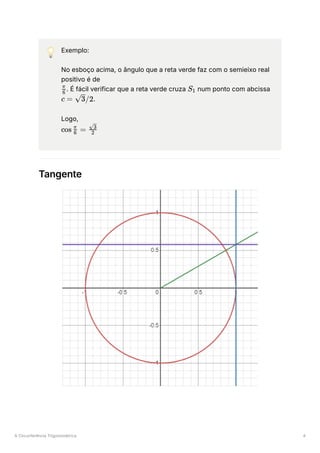
Do exercício anterior, já sabemos as soluções para a igualdade. Na
figura abaixo, podemos ver como utilizar a circunferência
trigonométrica para encontrar a solução da inequação, que está
assinalada a laranja:
Nota: não esquecer que, embora a tangente não admita argumentos
como e
, é importante lembrar que a equação original admite.
[0,2π[
sin (x) >
2
3 cos (x) ⟺
2
>
cos x
2
sin x
2
3 ⟺ tan x >
2
3 ⟺
⟺ tan x >
∨
3 tan x < −
3
S =] , [ ∪ ] , [
3
π
3
2π
3
4π
3
5π
2
π
2
3π](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-94-320.jpg)

![Funções Trigonométricas 1
Funções Trigonométricas
Funções Trigonométricas e os seus
Gráficos
Função Seno
A função seno é uma função real de variável real, que a cada valor de
associa o valor
:
A função seno é contínua e infinitamente diferenciável (ou seja, é
) em
(a função seno é
periódica)
(a função seno é ímpar)
Os limites não existem
A função seno tem máximos absolutos para
A função seno tem mínimos absolutos para
A função seno tem zeros para
Função Cosseno
x
sin (x)
D =
f R
D =
f
′
[−1,1]
C∞
R
sin(x + 2π) = sin(x),∀
x ∈ R 2π−
sin (−x) = − sin (x)
lim sin (x)
x⟶±∞
x = +
2
π
k2π, k ∈ Z
x = +
2
3π
k2π, k ∈ Z
x = kπ, k ∈ Z](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-96-320.jpg)
![Funções Trigonométricas 2
A função cosseno é uma função real de variável real, que a cada valor de
associa o valor
:
A função cosseno é contínua e infinitamente diferenciável (ou seja, é
)
em
(a função cosseno é
periódica)
(a função seno é ímpar)
Os limites não existem
A função seno tem máximos absolutos para
A função seno tem mínimos absolutos para
A função seno tem zeros para
Função Tangente
A função tangente é uma função real de variável real, que a cada valor de
associa o valor
:
x
cos(x)
D =
f R
D =
f
′
[−1,1]
C∞
R
cos(x + 2π) = cos(x),∀
x ∈ R 2π−
cos(−x) = cos(x)
lim
cos(x)
x⟶±∞
x = k2π, k ∈ Z
x = π + k2π, k ∈ Z
x = +
2
π
k2π, k ∈ Z
x
tan (x)](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-97-320.jpg)




![Sucessões de Números Reais 4
💡 Exemplo:
Pode-se provar por indução que
.
É imediato que a proposição é válida para
, já que
. Por isso, só é preciso provar
que se a proposição é válida para
, é válida para
:
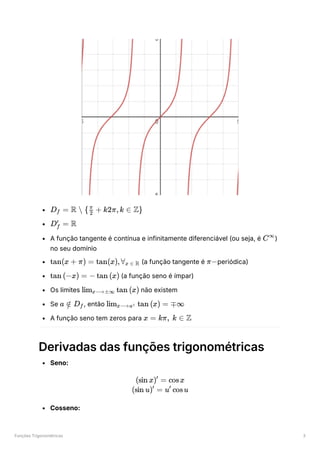
Progressão Aritmética
Dadas constantes reais e
, chama-se progressão aritmética de termo inicial
e razão à sucessão tal que:
Uma progressão aritmética tem a propriedade de que
, ou
seja, a diferença entre termos consecutivos é constante.
O termo geral de uma progressão aritmética de termo inicial e razão
,
:
A soma dos N primeiros termos de uma progressão aritmética é:
k =
∑k=1
n
2
n(n+1)
n = 1 k =
∑k=1
1
1 =
2
1(1+1)
n n + 1
k =
∑k=1
n
⟺
2
n(n+1)
(k) +
∑k=1
n
n + 1 =
+
2
n(n+1)
n + 1 ⟺
k =
∑k=1
n+1
+
2
n(n+1)
⟺
2
2(n+1)
k =
∑k=1
n+1
=
2
(n+2)(n+1)
□
2
(n+1)[(n+1)+1]
r a
a r u
n
{
u = a
1
u = u + r,
n+1 n ∀ n ∈ N
u
−
n+1 u
=
n r
a r u
n
u
=
n a + (n − 1) × r
u ≡
n=1
∑
N
n S =
N
×
2
(u + u
)
1 N
N](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-103-320.jpg)









![Derivadas e Aplicações 2
Se é diferenciável em
, então é contínua em
, de outro modo o limite
divergiria
Aos pontos tais que
, chamam-se pontos críticos de
💡 Exemplo:
Consideremos a função
. A derivada de em
,
, é dada pelo
limite:
A reta tangente ao gráfico de
em tem, portanto, equação:
Função Derivada
Dada uma função real de variável real
, a sua função derivada tem
domínio é diferenciável em
, e a cada faz
corresponder o valor
.
Se a função for contínua, diz-se que a função é continuamente
diferenciável, ou de classe
, e escreve-se
.
y = f(x
) +
0 f (x
)(x −
′
0 x
)
0
f x
0 x
0
x ∈ D
f f (x) =
′
0 f
f(x) = x +
2
x + 1 f x = 1 f (1)
′
lim
=
h⟶0 h
f(1+h)−f(1)
lim =
h⟶0 h
[(1+h) +1+h+1]−3
2
lim =
h⟶0 h
h +3h
2
= lim
h + 3 =
h⟶0 3
f x = 1
y = f(1) + f (1)(x −
′
1) = 3 + 3(x − 1) = 3x ⟺ y = 3x
f(x) f (x)
′
D =
f′ {x ∈ D :
f f x} x ∈ D
f′
f (x)
′
f (x)
′
f
C1
f ∈ C1](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-113-320.jpg)
![Derivadas e Aplicações 3
💡 Exemplo:
Consideremos a função
. A função derivada de
,
, obtém-se através
do limite:
Portanto,
. A reta tangente ao gráfico de em cada ponto
tem, nesse caso, equação:
Abaixo encontra-se uma animação com o gráfico da reta tangente em
função de
(representado por
).
f(x) = x +
2
x + 1 f f (x)
′
lim =
h⟶0 h
f(x+h)−f(x)
lim
=
h⟶0 h
[(x+h) +x+h+1]−x −x−1
2 2
= lim =
h⟶0 h
x +2hx+h +x+h+1−x −x−1
2 2 2
lim =
h⟶0 h
2hx+h +h
2
lim 2x + h + 1 =
h⟶0
= 2x + 1
f (x) =
′
2x + 1 f x
0
y = f(x
) +
0 f (x
)(x −
′
0 x
) =
0 x +
0
2
x +
0 1 + (2x +
0 1)(x −
x
) ⟹
0
⟹ y = x +
0
2
x +
0 1 + 2x
x +
0 x − 2x −
0
2
x ⟹
0 y = (1 +
2x
)x +
0 (1 − x
)
0
2
x
0 a](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-114-320.jpg)
![Derivadas e Aplicações 5
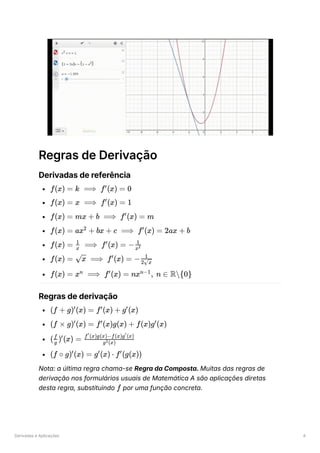
💡 Exemplos:
→ Tentemos calcular a derivada da função
:
Tivemos de utilizar as regras da composta e da potência.
→ Tentemos agora calcular a derivada da função
Tivemos de utilizar a regra do produto.
Teorema de Lagrange
Seja uma função diferenciável no intervalo aberto
, e contínua no
intervalo fechado
. Então:
Monotonia de uma Função Diferenciável
Seja uma função real de variável real contínua no intervalo fechado e
diferenciável no intervalo aberto
. Então:
f(x) =
1+x2
1
f (x) =
′
( ) =
1+x2
1 ′
((1 + x ) ) =
2 −
2
1
′
− ⋅
2
1
(1 + x ) (1 +
2 −
2
3
x ) =
2 ′
− ⋅
2
1
(1+x )
2
2
3
2x
f (x) =
′
−
(1+x )
2
2
3
x
f(x) = (x +
2
1)
x
f (x) =
′
((x +
2
1)
) =
x ′
(x +
2
1) +
′
x (x +
2
1)(
) =
x ′
2x +
x
2
x
x +1
2
f (a,b)
[a,b]
∃ :
c∈(a,b) f (c) =
′
b − a
f(b) − f(a)
f [a,b]
(a,b)](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-116-320.jpg)
![Derivadas e Aplicações 6
é estritamente crescente em
é estritamente decrescente em
é constante em
Determinação de extremos
Se for diferenciável em
, e for um extremo local de
, então
.
Se for crescente em e decrescente em
, então tem um
máximo relativo no ponto
Se for decrescente em e crescente em
, então tem um
mínimo relativo no ponto
∀
,f (x) >
x∈(a,b)
′
0 ⟹ f [a,b]
∀
,f (x) <
x∈(a,b)
′
0 ⟹ f [a,b]
∀
,f (x) =
x∈(a,b)
′
0 ⟹ f [a,b]
f x ∈
0 (a,b) x
0 f
f (x
) =
′
0 0
f [a,x
]
0 [x
,b]
0 f
x
0
f [a,x
]
0 [x
,b]
0 f
x
0](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-117-320.jpg)




![Derivadas e Aplicações 12
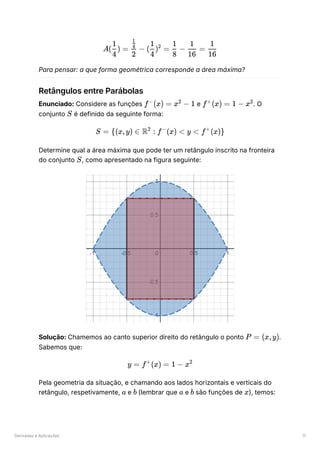
Então, a área do retângulo é, aplicando as restrições do problema,
, e dada pela seguinte expressão:
Estudamos agora a função quanto à monotonia:
0
Concluímos que a área máxima ocorre para
, ou seja:
Logo, a área máxima é
.
Boatos e Rumores
Enunciado: Sabe-se que a velocidade com que um rumor se espalha numa
população de pessoas é proporcional ao produto de pessoas que já ouviu o
rumor pelo número de pessoas que ainda não o ouviu, com constante de
proporcionalidade que depende da população em causa (será tanto maior
quanto mais mexeriqueiras foram as pessoas).
Determine quantas pessoas já ouviram o rumor, na altura em que a velocidade
com que ele se espalha é máxima.
Solução: Chamemos ao número de pessoas que já ouviu o boato
, ao número
de pessoas que ainda não o ouviu
, e à velocidade com que este se propaga
. O enunciado diz que
{
a(x) = 2x
b(x) = 2 ⋅ (1 − x )
2
A(a,b)
A(x)
A(x) = a(x) ⋅ b(x) = 2x ⋅ 2(1 − x ) =
2
4(x − x )
3
A(x) = 4(x − x )
3
A (x) =
′
0 ⟺ 4(1 − 3x ) =
2
0 ⟺ x =
2
⟹
3
1
x =
,(x >
3
3
0)
[0, [
3
3
3
3
[ , 1]
3
3
A (x)
′
+ −
A(x) ↗ Max ↘
x =
3
3
{
a( ) = 2
3
3
3
3
b( ) = 2 ⋅ (1 − ( ) ) = 2 ⋅ (1 − ) =
3
3
3
3 2
3
1
3
4
A( ) =
3
3
a( ) ⋅
3
3
b( ) =
3
3
2 ⋅
3
3
=
3
4
9
8
3
P
C
p
p
ˉ v
=
p ⋅
p
ˉ
v
C ⟺ v(p,
) =
p
ˉ C ⋅ p
p
ˉ](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-123-320.jpg)




![Limites, Continuidade e Assíntotas 4
Uma função é contínua num conjunto se for contínua em todos os pontos de
, e diz-se contínua se for contínua em todo o seu domínio.
💡 Exemplo:
A função
tem limites laterais diferentes quando
, logo não é
prolongável por continuidade a este ponto, isto é, não existe nenhum valor
tal que possamos definir uma função contínua da seguinte forma:
Operações com Funções Contínuas
Sejam e duas funções contínuas num ponto
. Então são contínuas em
:
, se
, com
Se for contínua em
, e for contínua em
:
é contínua em
Teorema de Bolzano(-Cauchy)
Seja uma função real de variável real, contínua num intervalo fechado
.
Então, para qualquer contido no intervalo de extremos e
, existe pelo
menos um tal que
.
Corolário do Teorema de Bolzano
Se é contínua no intervalo fechado
, e
, então existe pelo
menos um tal que
.
A ⊂ D
f
A
f(x) =
x
∣x∣
x ⟶ 0
k
f (x) =
#
{
f(x),
k,
x = 0
x = 0
f g a a
f + g
f − g
f × g
g
f
g(a) =
0
fr
r > 0
f a g f(a)
g ∘ f a
f [a,b]
k ∈ R f(a) f(b)
c f(c) = k
f [a,b] f(a) × f(b) < 0
c ∈ (a,b) f(c) = 0](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-128-320.jpg)

![Limites, Continuidade e Assíntotas 6
Note-se que pode estar definida em
, mas ser descontínua neste ponto.
💡 Exemplo:
O gráfico da função
tem uma assíntota vertical no ponto
, já que o limite
. Neste caso, tem assíntota aos dois lados, mas para
infinitos diferentes.
Assíntotas Não Verticais ao Gráfico de uma
Função
Dada uma função real de variável real
, diz-se que a equação é uma
assíntota não vertical ao gráfico de em se:
Os valores de e são dados pelos seguintes limites, caso eles existam e sejam
finitos (caso contrário, a função não tem assíntota não vertical em
:
No caso
, diz-se que a assíntota é horizontal, e neste caso
.
f a
f(x) =
x
e−x
x = 0
lim
f(x) =
x⟶0± ±∞
f y = mx + b
f ±∞
[f(x) −
f⟶±∞
lim (mx + b)] = 0
m b
±∞
{
m = lim
x⟶±∞ x
f(x)
b = lim
(f(x) − mx)
x⟶±∞
m = 0 lim f(x) =
x⟶∞ b](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-130-320.jpg)












![Espaços de probabilidades e Definição de Laplace 5
Propriedades da função Probabilidade
Probabilidade de um acontecimento contrário:
Probabilidade do conjunto vazio:
A probabilidade dum acontecimento está sempre entre 0 e 1:
A probabilidade dum acontecimento pode ser dada por:
Se
:
P =
84
65
P( ) =
A 1 − P(A)
P(Ø) = 0
∀A ∈ P(E),P(A) ∈ [0,1]
P(A) = P(A ∩ B) + P(A ∩ )
B
A ⊂ B
P(BA) = P(B) − P(A)
P(A) ≤ P(B)](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-143-320.jpg)





















![Representação Geométrica 2
Ao eixo
, o eixo vertical, chama-se o eixo imaginário.
Ao eixo
, o eixo horizontal, chama-se o eixo real.
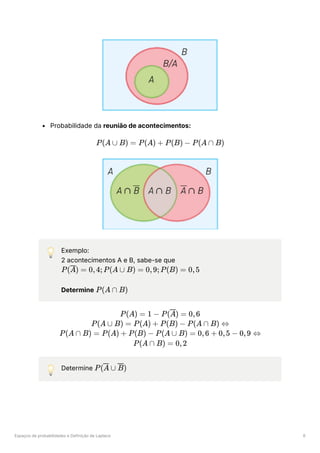
Argumento de um Número Complexo
Seja o afixo do número complexo
.
Define-se o argumento de
,
, como o ângulo formado entre o eixo real
e o segmento
. Como este ângulo pode ter muitos valores, chama-se o
argumento principal de a se e só se
. Nesse caso,
:
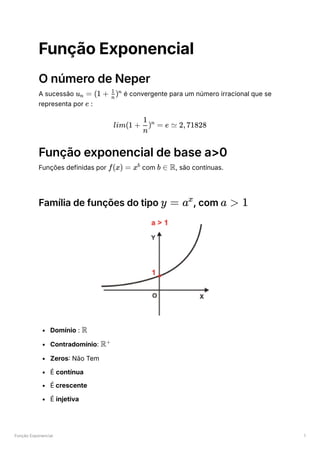
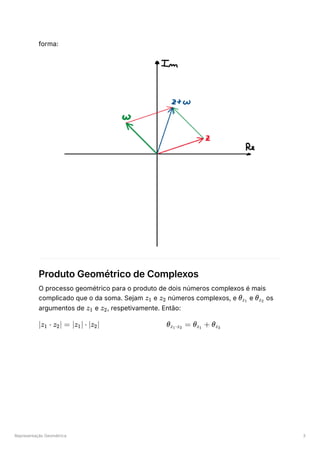
Soma Geométrica de Complexos
O processo geométrico para a soma de dois números complexos é idêntico ao
da soma de vetores em
: dados
, representa-se da seguinte
(0,y)
(x,0)
∣∣(a,b)∣∣ =
=
a + b
2 2 ∣z∣
P z = x + iy
z arg z θ
OP
z θ θ = arg z ∧ θ ∈ ] − π,π]
θ = arctan
x
y
R2
z,w ∈ C z + w](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-167-320.jpg)

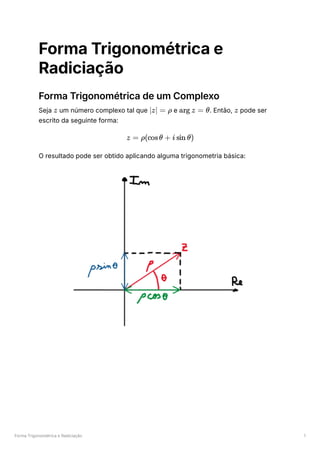







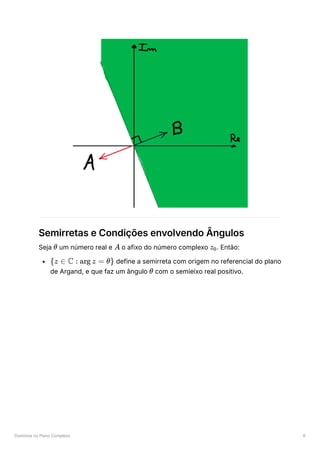
![Domínios no Plano Complexo 3
Retas e Semiplanos
Sejam e os afixos de dois números complexos distintos, e
,
respetivamente. Então:
define, no plano complexo, a mediatriz do
segmento de reta
.
A B z
1 z
2
{z ∈ C : ∣z − z
∣ =
1 ∣z − z
∣}
2
[AB]](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-180-320.jpg)
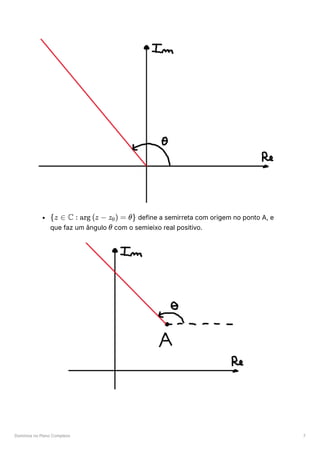
![Domínios no Plano Complexo 4
define, no plano complexo, o conjunto dos
pontos mais próximos de (ou a uma igual distância entre e
), ou seja,
o semiplano definido pela mediatriz do segmento de reta que contém
o ponto
.
{z ∈ C : ∣z − z
∣ ≤
1 ∣z − z
∣}
2
A A B
[AB]
A](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-181-320.jpg)
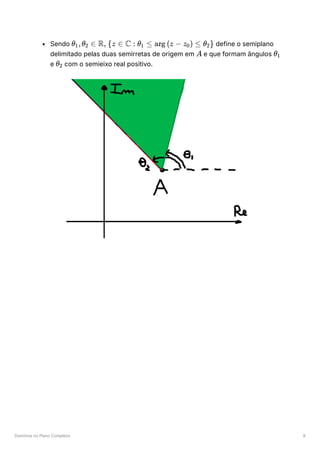
![Domínios no Plano Complexo 5
define, no plano complexo, o conjunto dos
pontos mais próximos de
, ou seja, o semiplano definido pela mediatriz do
segmento de reta que contém o ponto (mas não a própria
mediatriz).
{z ∈ C : ∣z − z
∣ >
1 ∣z − z
∣}
2
B
[AB] B](https://image.slidesharecdn.com/teoricamat-240521214151-6fbf4570/85/teorica-completa-de-matematica-A-do-secundario-182-320.jpg)