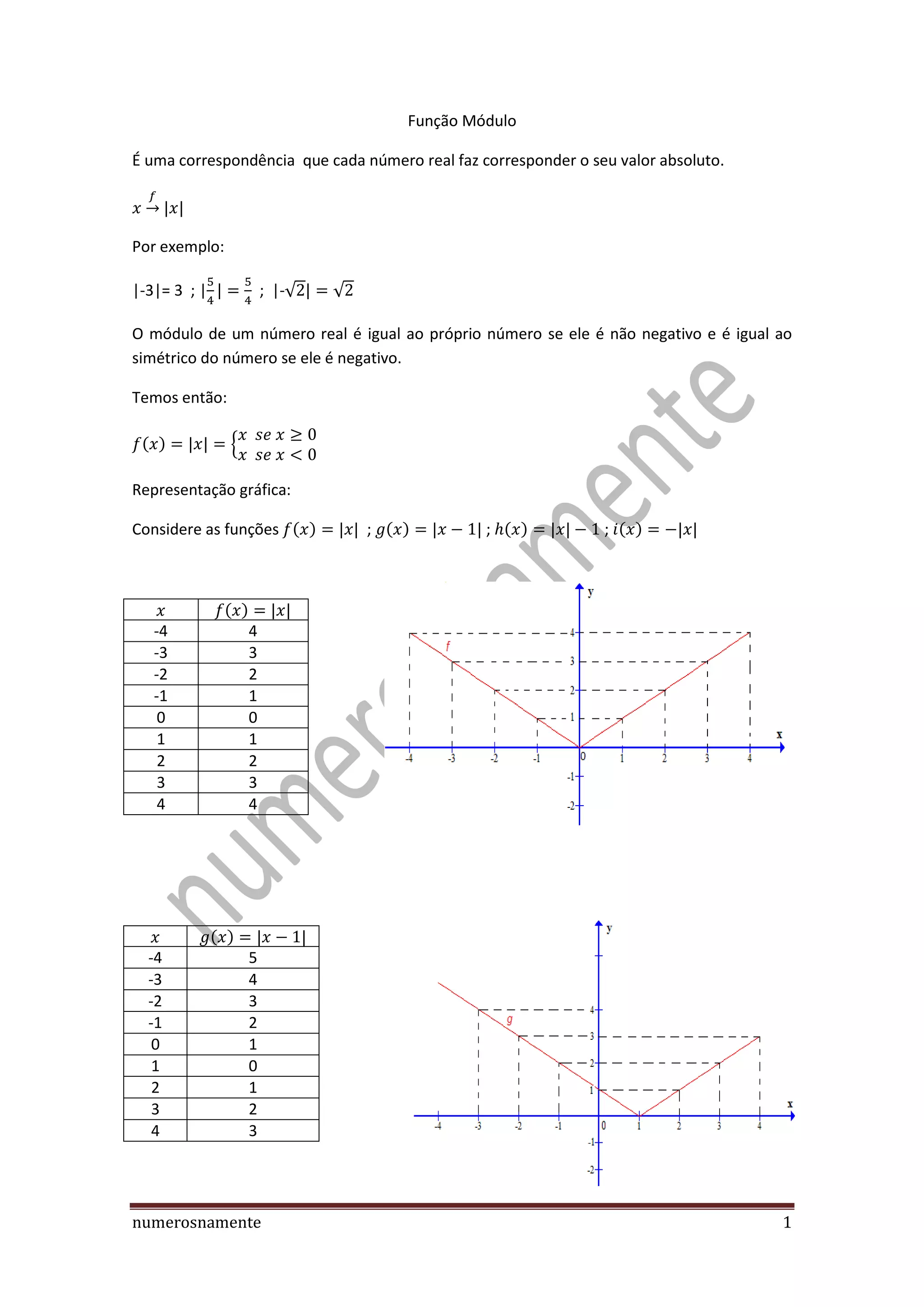
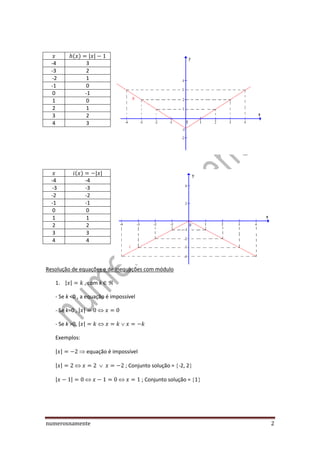
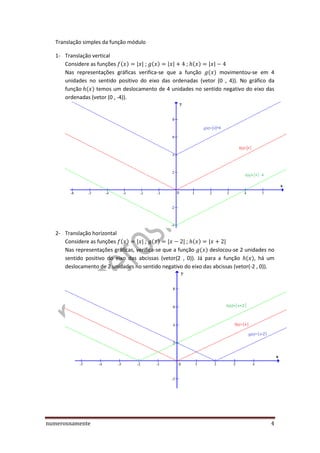
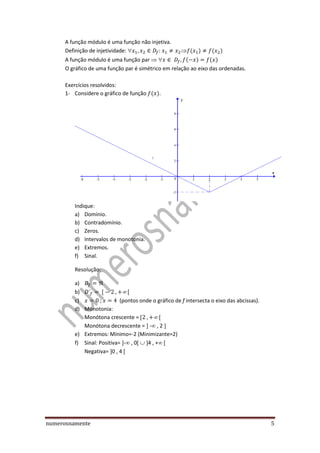
O documento apresenta os conceitos e propriedades da função módulo, incluindo: (1) sua definição como correspondendo ao valor absoluto de um número real; (2) resolução de equações e inequações envolvendo módulo; (3) translação da função módulo; (4) função módulo não ser injetiva por ser par. Exemplos ilustram os conceitos apresentados.

1. numerosnamente 1
Função Módulo
É uma correspondência que cada número real faz corresponder o seu valor absoluto.
→
Por exemplo:
|-3|= 3 ; | ; |-√ √
O módulo de um número real é igual ao próprio número se ele é não negativo e é igual ao
simétrico do número se ele é negativo.
Temos então:
( ) {
Representação gráfica:
Considere as funções ( ) ; ( ) ; ( ) ; ( )
( )
-4 4
-3 3
-2 2
-1 1
0 0
1 1
2 2
3 3
4 4
( )
-4 5
-3 4
-2 3
-1 2
0 1
1 0
2 1
3 2
4 3

2. numerosnamente 2
Resolução de equações e de inequações com módulo
1. , com k
- Se k <0 , a equação é impossível
- Se k=0 ,
- Se k >0,
Exemplos:
 equação é impossível
; Conjunto solução = -2, 2
; Conjunto solução = 1
( )
-4 3
-3 2
-2 1
-1 0
0 -1
1 0
2 1
3 2
4 3
( )
-4 -4
-3 -3
-2 -2
-1 -1
0 0
1 1
2 2
3 3
4 4

3. numerosnamente 3
2. , com k
- Se , a condição é impossível
- Se
Exemplos:
 a condição é impossível
Conjunto solução =
- -1 3 + 
3. , com k
- Se , a condição é universal e o conjunto solução é
- Se  
- Se
Exemplos:
, a condição é universal ; Conjunto solução =
; Conjunto solução: 
Conjunto solução:  
- -3 1 +

4. numerosnamente 4
Translação simples da função módulo
1- Translação vertical
Considere as funções ( ) ; ( ) ; ( )
Nas representações gráficas verifica-se que a função ( ) movimentou-se em 4
unidades no sentido positivo do eixo das ordenadas (vetor (0 , 4)). No gráfico da
função ( ) temos um deslocamento de 4 unidades no sentido negativo do eixo das
ordenadas (vetor (0 , -4)).
2- Translação horizontal
Considere as funções ( ) ; ( ) ; ( )
Nas representações gráficas, verifica-se que a função ( ) deslocou-se 2 unidades no
sentido positivo do eixo das abcissas (vetor(2 , 0)). Já para a função ( ), há um
deslocamento de 2 unidades no sentido negativo do eixo das abcissas (vetor(-2 , 0)).

5. numerosnamente 5
A função módulo é uma função não injetiva.
Definição de injetividade:   ( ) ( )
A função módulo é uma função par   ( ) ( )
O gráfico de uma função par é simétrico em relação ao eixo das ordenadas.
Exercícios resolvidos:
1- Considere o gráfico de função ( ).
Indique:
a) Domínio.
b) Contradomínio.
c) Zeros.
d) Intervalos de monotonia.
e) Extremos.
f) Sinal.
Resolução:
a)
b) 
c) (pontos onde o gráfico de f intersecta o eixo das abcissas).
d) Monotonia:
Monótona crescente = 
Monótona decrescente = - , 2
e) Extremos: Mínimo=-2 (Minimizante=2)
f) Sinal: Positiva= - , 0 4 , +
Negativa= 0 , 4

6. numerosnamente 6
2- Considere a função ( )
a) Indique o domínio.
b) Resolva ( )
c) Resolva ( )
Resolução:
a)
b)
;  
c)
;
3- Determine o conjunto solução da equação:
Resolução:
 
4- Determine o conjunto solução da inequação:
Resolução:
; Conjunto solução:
5- Considere a função ( )
a) Escreva a função g sem usar módulos.
b) Calcule ( ) ( ) ( )
c) Calcule ( ) ; ( ) ;  ( )  ( )
Resolução:
a) ( ) {
( )
( )
{
b) ( ) ( )
( ) ( )
( ) ( )
c) ( ) ( ) ( )
( ) ( )
 ( ) (  )   ( ) ( ( ) ) 