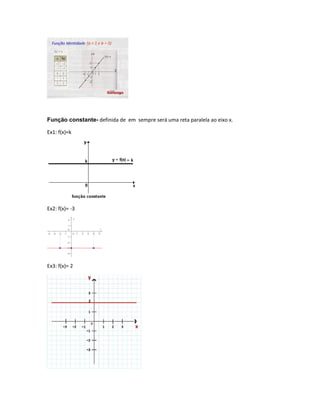
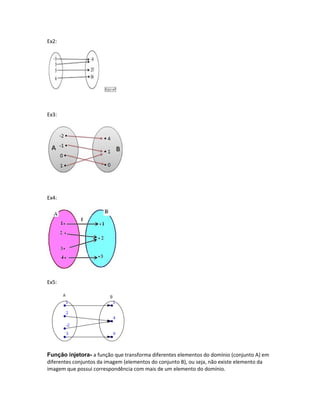
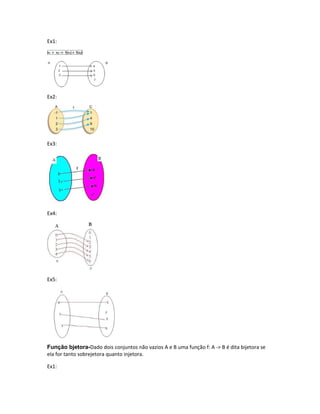
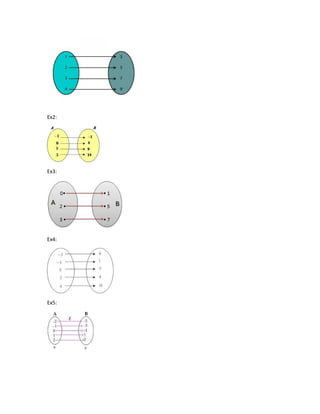
O documento descreve diferentes tipos de funções polinomiais e suas propriedades, incluindo grau de uma função, função identidade, função constante, função modular, função composta, função sobrejetora, função injetora e função bijetora. Exemplos ilustram cada tipo de função.

1. PARTE 7
Função polinomial- Toda função na forma P(x) = anxn + an-1xn-1 + ... + a2x2 + a1x + a0 é
considerada uma função polinomial, onde p(x) está em função do valor de x.
Ex1: g(x) = 4x4 + 10x2 – 5x + 2.
Ex2: f(x) = -9x6 + 12x3 - 23x2 + 9x – 6.
EX3: h(x) = -3x3 + 9x2 – 5x + 6.
EX4: p(x) = 2x3 + 2x2 – 5x + 1.
Ex5: k(x) = 2x3 + 5x2 + 2x - 9.
Grau de uma função- O grau de um polinômio é expresso através do maior expoente natural
entre os monômios que o formam.
Ex1:g(x) = 4x4 + 10x2 – 5x + 2. grau: 4
Ex2:f(x) = -9x6 + 12x3 - 23x2 + 9x – 6. grau: 6
Ex3: h(x) = -3x3 + 9x2 – 5x + 6. grau: 3
Ex4:p(x) = 2x3 + 2x2 – 5x + 1. grau: 3
Ex5: k(x) = 2x3 + 5x2 + 2x - 9. grau: 3
Função identidade- Uma função f de em recebe
o nome de FUNÇÃO IDENTIDADE
quando associa a cada elemento x E R o próprio x.
Ex1:
Ex2:

2. Ex3:
Ex4:
Ex5:

3. Função constante- definida de em sempre será uma reta paralela ao eixo x.
Ex1: f(x)=k
Ex2: f(x)= -3
Ex3: f(x)= 2

4. Ex4: f(x)= 4
EX5: f(x)=0
Funções definidas por mais de uma- Uma função f pode ser definida por várias sentenças
abertas, cada uma das quais está ligada
a um domínio D, contido no domínio da f.
Ex1:

5. Ex2:
Ex3:
Ex4:
Ex5:

6. Modulo- Chamamos a distância de um ponto da reta à origem (distância do ponto até o zero)
de módulo ou valor absoluto.
Ex1: |4| = 4
Ex2:|-2| = 2
Ex3:|3| = 3
Ex4:|-7| = 7
Ex5:|0| = 0
Função modular- Estabelecemos uma função através da relação entre duas grandezas (duas
incógnitas), sendo que uma incógnita será dependente e essa terá que estar relacionada com
apenas um valor que será a incógnita independente. Seguindo essa definição, será considerada
função modular toda função onde essa incógnita independente estiver dentro de módulos.
Ex1:f(x) = |x -1|
Ex2:f(x) = |x – 3| + 2
Ex3:f(x) = x2/|x|
Ex4:f(x) = |2x2 – 4x|
Ex5: f(x) = |x2 – 3x|
PARTE 8
Função composta- temos que f: A → B e g: B → C, denomina a formação da função composta

7. de g com f, h: A → C. Dizemos função g composta com a função f, representada por gof.
Ex1:Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
g o f
(g o f)(x) = g(f(x))
g(x) = x² + 5
g(4x) = (4x)² + 5
g(4x) = 16x² + 5
(g o f)(x) = g(f(x)) = 16x² + 5
Ex2:Ao considerarmos as funções f(x) = 4x e g(x) = x² + 5, determinaremos:
f o g
(f o g)(x) = f(g(x))
f(x) = 4x
f(x² + 5) = 4 * (x² + 5)
f(x² + 5) = 4x² + 20
(f o g)(x) = f(g(x)) = 4x² + 20
Ex3:Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(g o f)(x) = g(f(x))
g(x) = 4x² – 1
g(x + 2) = 4 * (x + 2)² – 1
g(x + 2) = 4 * (x + 2) * (x + 2) – 1
g(x + 2) = 4 * (x² + 2x + 2x + 4) – 1
g(x + 2) = 4 * (x² + 4x + 4) – 1
g(x + 2) = 4x² + 16x + 16 – 1

8. g(x + 2) = 4x² + 16x + 15
(g o f)(x) = g(f(x)) = 4x² + 16x + 15
Ex4:Vamos determinar g(f(x)) e f(g(x)), em relação às funções f(x) = x + 2 e g(x) = 4x² – 1.
(f o g)(x) = f(g(x))
f(x) = x + 2
f(4x² – 1) = (4x² – 1) + 2
f(4x² – 1) = 4x² – 1 + 2
f(4x² – 1) = 4x² + 1
(f o g)(x) = f(g(x)) = 4x² + 1
Ex5: Dadas as leis das funções f e g:
f(x) = 2x
g(x) = x – 14.
Obter (f ο g)(x)
(f ο g)(x) = f(g(x)) = 2g(x) = 2(x – 14) = 2x – 28.
Função sobrejetora- Uma função é dita sobrejetora quando o contradomínio da função for
igual ao conjunto imagem. Em outras palavras uma função é sobrejetora quando todo elemento
de B é imagem de pelo menos um elemento de A.
Ex1:

9. Ex2:
Ex3:
Ex4:
Ex5:
Função injetora- a função que transforma diferentes elementos do domínio (conjunto A) em
diferentes conjuntos da imagem (elementos do conjunto B), ou seja, não existe elemento da
imagem que possui correspondência com mais de um elemento do domínio.

10. Ex1:
Ex2:
Ex3:
Ex4:
Ex5:
Função bjetora-Dado dois conjuntos não vazios A e B uma função f: A -> B é dita bijetora se
ela for tanto sobrejetora quanto injetora.
Ex1:

11. Ex2:
Ex3:
Ex4:
Ex5: