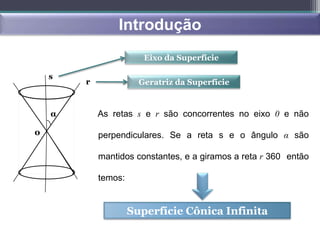
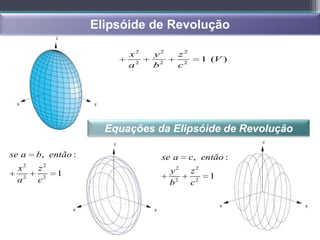
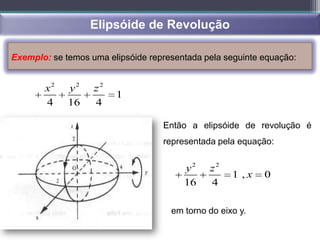
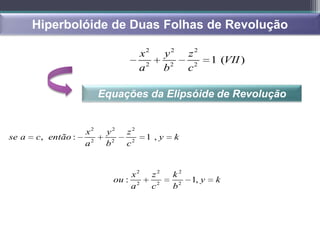
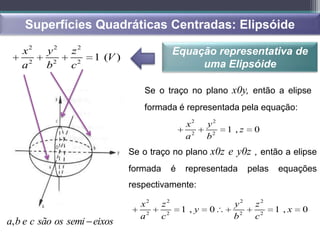
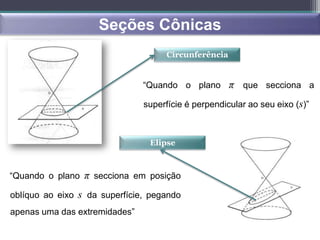
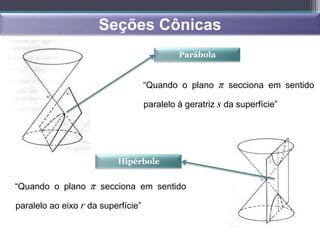
- Superfícies quadráticas, cônicas, cilíndricas, esféricas e de rotação são introduzidas. - Superfícies quadráticas podem ser centradas ou não centradas e incluem elipsóides, hiperbóides e parabóides. - Seções cônicas incluem circunferências, elipses, parábolas e hipérboles. - Superfícies cilíndricas são definidas por uma diretriz e geratrizes paralelas.

1. Superfícies
GET 003 – Geometria Analítica e Álgebra Linear
Prof. Kátia Dionísio de Oliveira - FAMAT / UFU
Maio - 2012

2. SUMÁRIO
 Superfícies:
• Quadráticas
• Cônicas
• Cilíndricas
• Esféricas
• De Rotação

3. Introdução
Eixo da Superfície
s
r Geratriz da Superfície
α As retas s e r são concorrentes no eixo 0 e não
0 perpendiculares. Se a reta s e o ângulo α são
mantidos constantes, e a giramos a reta r 360 então
temos:
Superfície Cônica Infinita

4. Seções Cônicas
Circunferência
“Quando o plano π que secciona a
superfície é perpendicular ao seu eixo (s)”
Elipse
“Quando o plano π secciona em posição
oblíquo ao eixo s da superfície, pegando
apenas uma das extremidades”

5. Seções Cônicas
Parábola
“Quando o plano π secciona em sentido
paralelo à geratriz s da superfície”
Hipérbole
“Quando o plano π secciona em sentido
paralelo ao eixo r da superfície”

6. Superfícies Quadráticas: Introdução
Nesta parte da matéria estudaremos as superfícies que podem ser
representadas por equações do tipo:
ax 2 by 2 cz 2 2dxy 2exz 2 fyz mx ny pz q 0 I
a, b, c, d , e ou f 0
e representam uma superfície quadrática. Por sua vez se esta superfície
for seccionada por um plano π, já vimos que a curva de interseção
formará uma cônica. E a interseção da superfície com um plano é
denominada de traço na superfície no plano.

7. Superfícies Quadráticas: Introdução
Exemplo: se temos um plano e a coordenada z é 0, então a cônica
formada é representada pela seguinte equação:
ax 2 by 2 2dxy mx ny q 0
a, b, d , m, n 0 plano x0 z
“Por outro lado se as coordenadas forem alteradas por movimentos de
rotação ou translação da superfície, a equação I pode ser reescrita da
seguinte maneira”:

8. Superfícies Quadráticas: Introdução
Ax2 By 2 Cz 2 D (II ) Quadrática Centrada
Ax 2 By 2 Rz 0
Ax 2 Ry Cz 2 0 ( III )
2 2
Quadráticas Não Centradas
Rx By Cz 0
“O objetivo é esboçar um gráfico a partir do conhecimento das equações
quadráticas:
Quadráticas Centradas
Quadráticas Não Centradas

9. Superfícies Quadráticas Centradas: Introdução
Ax2 By 2 Cz 2 D (II ) “Se nenhum dos coeficientes da equação
II for 0, então a equação ao lado poderá
ser reescrita da seguinte maneira:”
Forma Canônica ou Padrão x2 y2 z2
1 ( IV )
de Superfície Quadrática a2 b2 c2
“Neste caso, somente existem apenas três tipos de combinações de sinais
nesta equação o que permitem concluir apenas existência de três
superfícies. Por outro lado, se todos os coeficientes fossem negativos, não
haveria lugar geométrico”.

10. Superfícies Quadráticas Centradas: Elipsóide
x2 y2 z2 Equação representativa de
1 (V )
a2 b2 c2 uma Elipsóide
Se o traço no plano x0y, então a elipse
formada é representada pela equação:
x2 y2
1 ,z 0
a2 b2
Se o traço no plano x0z e y0z , então a elipse
formada é representada pelas equações
respectivamente:
x2 z2 y2 z2
1 ,y 0 1 ,x 0
a2 c2 b2 c2
a, b e c são os semi eixos

11. Elipsóide de Revolução
x2 y2 z2
1 (V )
a2 b2 c2
Equações da Elipsóide de Revolução
se a b, então : se a c, então :
x2 z2 y2 z2
1 1
a2 c2 b2 c2

12. Elipsóide de Revolução
Exemplo: se temos uma elipsóide representada pela seguinte equação:
x2 y2 z2
1
4 16 4
Então a elipsóide de revolução é
representada pela equação:
y2 z2
1 ,x 0
16 4
em torno do eixo y.

13. Elipsóide de Revolução
O traço do plano x0z é a circunferência representada pela equação:
x2 z2
1, y 0
4 4
Então o lugar geométrico Se a b c, então :
representa uma superfície esférica x2 y2 z2 a2
de centro (0, 0, 0) raio a
Se o centro da elipsóide é
2 2 2
x h y k z l
1 representado pela coordenada (h, k, l)
a2 b2 c2
e seus eixos forem paralelos ao eixo
2 2 2
x h y k z l a2 das coordenadas, então:

14. Superfícies Quadráticas Centradas:
Hiperbolóide de uma Folha
x2 y2 z2 Equação representativa de
1 (VI ) uma Hiperbolóide de 1 Folha
a2 b2 c2
x2 y2 z2
1
a2 b2 c2
x2 y2 z2
1
a2 b2 c2

15. Superfícies Quadráticas Centradas:
Hiperbolóide de uma Folha
x2 y2 Se o traço no plano x0y, é a elipse
1 ,z 0
a2 b2 representada pela equação:
Se o traço no plano x0z, e y0z são as hipérboles representadas pelas
respectivas equações:
x 2
z2 y2 z2
1 ,y 0 1 ,x 0
a2 c2 b2 c2

16. Hiperbolóide de Revolução
x2 y2 z2
1 (VI )
a2 b2 c2
Equações da Elipsóide de Revolução
x2 y2
se a b, então : 2 1 ,z 0
a b2
ou : x2 y2 a2 , z 0

17. Superfícies Quadráticas Centradas:
Hiperbolóide de duas Folhas
x2 y2 z2 Equação representativa de
1 (VII ) uma Hiperbolóide de 2 Folhas
a2 b2 c2
x2 y2 z2
1
a2 b2 c2
x2 y2 z2
1
a2 b2 c2

18. Superfícies Quadráticas Centradas:
Hiperbolóide de duas Folhas
Se o traço no plano x0y e y0z, é a elipse representada pelas respectivas
equações:
y 2
x2 y2 z2
1 ,z 0 1 ,x 0
b2 a2 b2 c2

19. Hiperbolóide de Duas Folhas de Revolução
x2 y2 z2
1 (VII )
a2 b2 c2
Equações da Elipsóide de Revolução
x2 y2 z2
se a c, então : 1 ,y k
a2 b2 c2
x2 z2 k2
ou : 2 1, y k
a c2 b2

20. Superfícies Quadráticas Não Centradas: Introdução
Ax 2 By 2 Rz 0 “Se nenhum dos coeficientes da
Ax 2 Ry Cz 2 0 ( III ) equação III for 0, então a equação
Rx By 2 Cz 2 0 ao lado poderá ser reescrita da
seguinte maneira:”
x2 y2 x2 z2 y2 z2
cz; by; ax (VIII )
a2 b2 a2 c2 b2 c2
“Neste caso, somente existem apenas 2 tipos de combinações de sinais
nesta equação o que permitem concluir apenas existência de dois
superfícies”.

21. Superfícies Quadráticas Não Centradas:
Parabolóide Elíptica
“Se na equação anterior dois coeficientes tiverem sinais iguais então a
equação abaixo:”
x2 y2 Equação representativa de
cz
a2 b2 uma Parabolóide Elíptica
Se o traço do plano x0y é a origem (0, 0, 0) e
os traços nos planos x0z e y0y são as
parábolas representadas pelas equações
abaixo, respectivamente:
x 2 y2
cz , y 0 cz , x 0
a2 b2

22. Superfícies Quadráticas Não Centradas:
Parabolóide Elíptica e Hiperbólico
x2 y2
Se na equação cz , a=b, então a parabolóide é de
a2 b2
revolução e pode ser gerado pela rotação da parábola representada
pela equação abaixo: y2
2
cz , x 0
b
Se na equação x2 y2 x2 z 2 y2 z2
cz; by; ax (VIII )
a2 b 2 2
a c 2
b2 c2
Tiverem sinais contrários então caracteriza-se uma equação
PARABOLÓIDE HIPERBÓLICA
x2 y2
cz
a2 b2

23. Superfícies Quadráticas Não Centradas:
Parabolóide Hiperbólico
As equações abaixo representam 0y e 0x, respectivamente as
parábolas representadas pelas equações abaixo, respectivamente:
z2 x2 z2 y2
by ax
c2 a2 c2 b2

24. Exercícios (2,0 pontos em dupla)
1) Faça um esboço do gráfico da seguinte equação e dê nome a
2
superfície: 4 x y2 25z 2 100
2) Faça um esboço do gráfico da seguinte equação e dê nome a
superfície: 4 x2 25 y 2 z2 100
3) Faça um esboço do gráfico da seguinte equação e dê nome a
superfície: 3 y2 12 z 2 16 x
4) Faça um esboço do gráfico da seguinte equação e dê nome a
superfície: 3 y2 12 x 2 16 z

25. Superfícies Cilíndricas
Definição: Dado um subconjunto S
¡ , 3
contido em tal que reúne retas paralelas S W
a uma reta W não situada no plano da
curva. Este subconjunto pode ser
considerado uma superfície cilíndrica se
existir uma curva C pela qual as retas C
paralelas de S passem. Neste contexto,
C é diretriz de S , cujas retas paralelas
são chamadas de geratrizes da
superfície cilíndrica.

26. Superfícies Cilíndricas
Exemplo: Um cilindro quadrático pode ser definido como um conjunto
de pontos do espaço, cujas coordenadas satisfaçam a seguinte equação:
f ( x, y ) 0
em que a equação acima representa uma cônica no plano XY. Por outro
lado se fixarmos, um sistema de coordenadas e supondo que:
f ( x, y , z ) 0
C é definido por :
g ( x, y , z ) 0
 
v m, n, p 0 é um vetor diretor da reta W

27. Superfícies Cilíndricas
Então, P S se somente se Q Î C e l Î ¡ de modo
que: 
 
PQ v
(x X , y Y , z Z ) m, n, p
W
Logo:
x X m
y Y n
z Z p

28. Superfícies Cilíndricas
Como: f ( x, y, z ) 0
C é definido por :
g ( x, y, z ) 0
f (X m, Y n, Z p) 0
g( X m, Y n, Z p) 0
Se pudéssemos eliminar λ, chegaríamos a um equação do tipo:
f ( x, y, z ) 0
g ( x, y, z ) 0
Ou seja, existe um valor de λ que satisfaz o sistema descrito anteriormente

29. Exercícios (3,0 pontos em dupla)
1) Ache uma equação da superfície cilíndrica de diretriz :
x2 y2 z2 4
C :
z 0
cujas as geratrizes são paralelas à reta W:
x
y 1
z 2

30. 2) Ache uma equação da superfície cilíndrica de geratrizes paralelas ao

vetor v 2, 1,1 e circunscrita à superfície esférica:
x2 y2 z2 1
3) Verifique que uma relação do tipo F(x,y) = 0 é equação de uma
superfície cilíndrica S de diretriz:
e geratrizes paralelas a Oz. Represente
F ( x, y ) 0 no plano Oxy os pontos (x, y, 0) tais que
C:
z 0
F(x,y) = 0 e trace as retas que passam
por eles e são paralelas a Oz. A
superfície S é a reunião dessas retas.