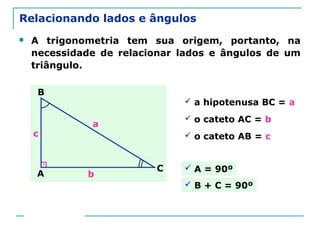
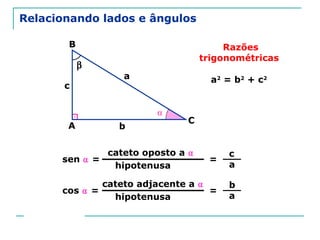
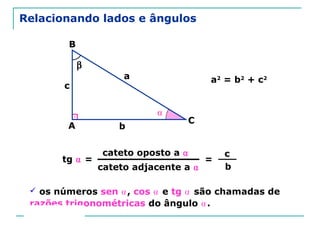
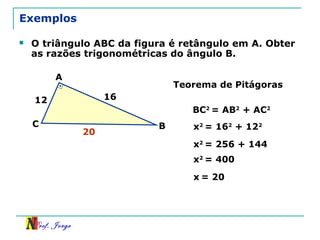
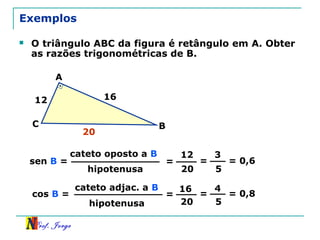
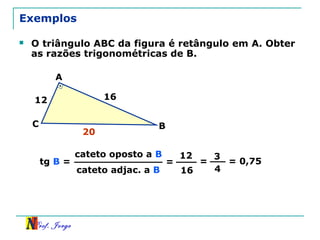
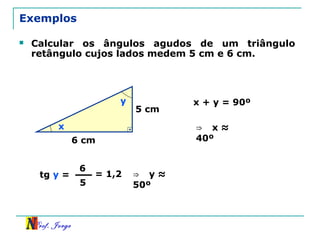
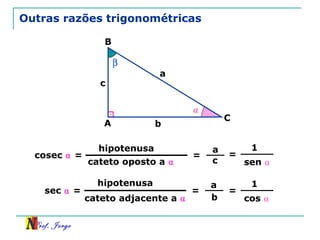
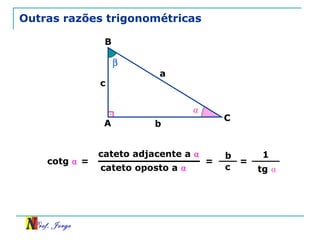
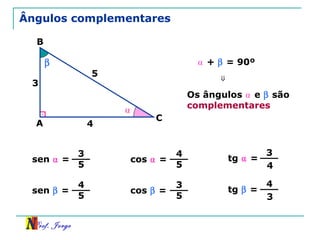
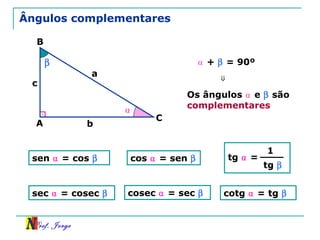
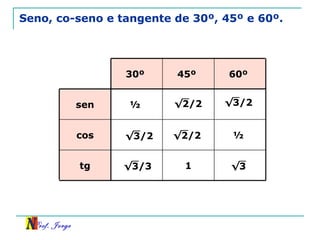
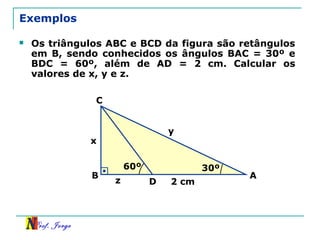
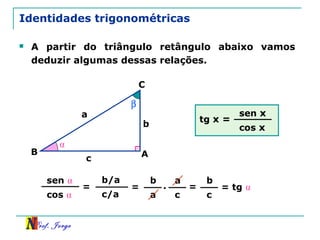
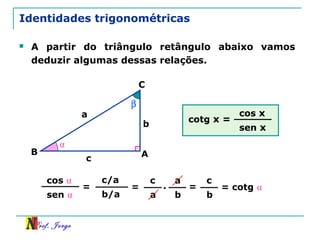
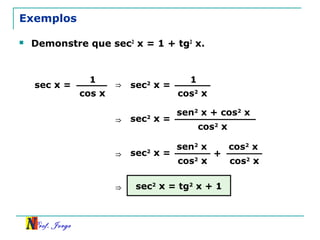
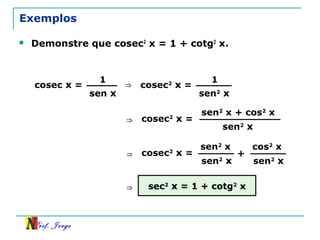
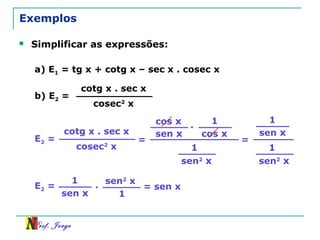
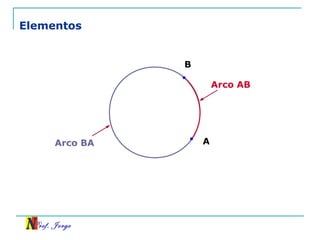
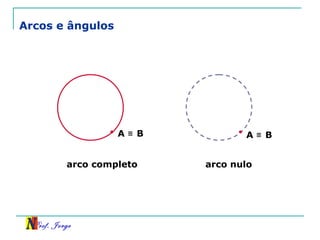
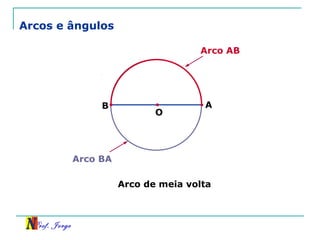
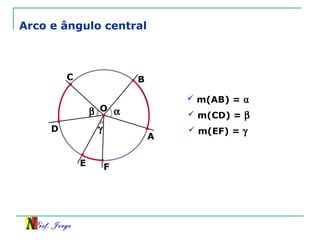
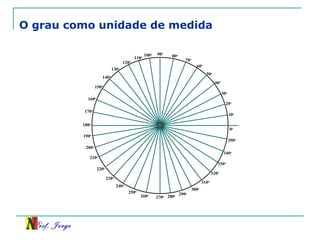
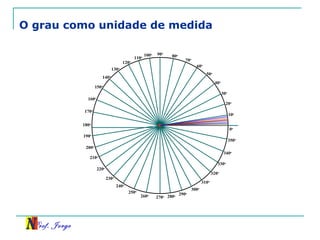
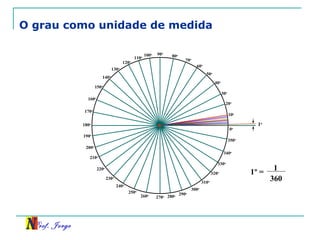
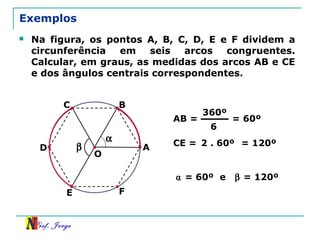
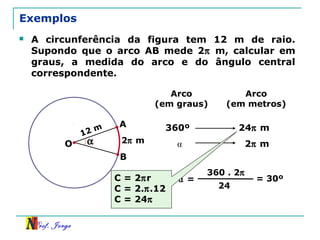
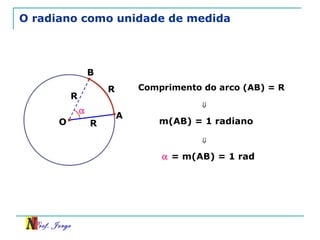
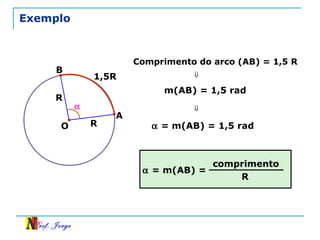
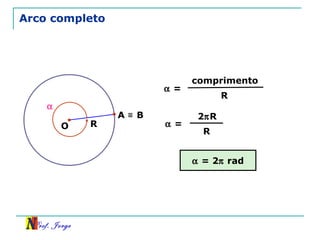
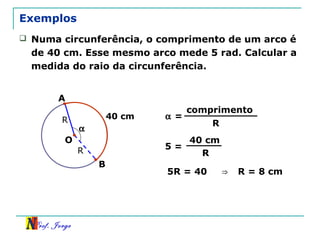
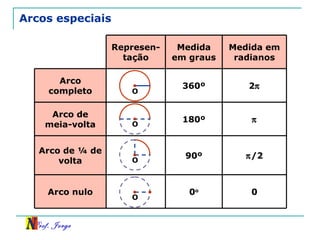
O documento discute trigonometria em triângulos retângulos. Explica como a trigonometria relaciona os lados e ângulos de um triângulo retângulo, introduzindo as razões trigonométricas seno, cosseno e tangente. Também apresenta identidades trigonométricas e exemplos de cálculos envolvendo triângulos retângulos e suas razões.

1. Prof. Jorge
Trigonometria no
Triângulo Retângulo

2. Prof. Jorge
 Contexto historico
Surgimento da Trigonomia
Qual ferramenta utilizada na
Trigonometria?

3. Prof. Jorge
Relacionando lados e ângulos
 A trigonometria tem sua origem, portanto, na
necessidade de relacionar lados e ângulos de um
triângulo.
 a hipotenusa BC = a
A
B
C
a
b
c
 o cateto AC = b
 o cateto AB = c
 A = 90º
 B + C = 90º

4. Prof. Jorge
Relacionando lados e ângulos
A
B
C
a
b
c
a2
= b2
+ c2
⍺
cateto oposto a ⍺
hipotenusa
=sen ⍺ =
c
a
cateto adjacente a ⍺
hipotenusa
=cos ⍺ =
b
a
β
Razões
trigonométricas

5. Prof. Jorge
Relacionando lados e ângulos
A
B
C
a
b
c
a2
= b2
+ c2
⍺
cateto oposto a ⍺
=tg ⍺ =
c
bcateto adjacente a ⍺
β
 os números sen ⍺, cos ⍺ e tg ⍺ são chamadas de
razões trigonométricas do ângulo ⍺.

6. Prof. Jorge
Exemplos
 O triângulo ABC da figura é retângulo em A. Obter
as razões trigonométricas do ângulo B.
12 16
A
BC
Teorema de Pitágoras
BC2
= AB2
+ AC2
x2
= 162
+ 122
x2
= 256 + 144
x2
= 400
x = 20
20

7. Prof. Jorge
Exemplos
 O triângulo ABC da figura é retângulo em A. Obter
as razões trigonométricas de B.
cateto oposto a B
hipotenusa
sen B = =
12
20
=
3
5
= 0,6
cateto adjac. a B
hipotenusa
cos B = =
16
20
=
4
5
= 0,8
12 16
A
BC
20

8. Prof. Jorge
Exemplos
 O triângulo ABC da figura é retângulo em A. Obter
as razões trigonométricas de B.
cateto oposto a B
cateto adjac. a B
tg B = =
12
16
=
3
4
= 0,75
12 16
A
BC
20

9. Prof. Jorge
Exemplos
 Calcular os ângulos agudos de um triângulo
retângulo cujos lados medem 5 cm e 6 cm.
5 cm16
6 cm
x
y
tg y =
6
5
= 1,2 ⇒ y ≈
50º
x + y = 90º
⇒ x ≈
40º

10. Prof. Jorge
Outras razões
trigonométricas

11. Prof. Jorge
β
Outras razões trigonométricas
A
B
C
a
b
c
⍺
cateto oposto a ⍺
hipotenusa
=cosec ⍺ =
a
c
cateto adjacente a ⍺
hipotenusa
=sec ⍺ =
a
b
=
1
sen ⍺
=
1
cos ⍺

12. Prof. Jorge
β
Outras razões trigonométricas
A
B
C
a
b
c
⍺
cateto oposto a ⍺
=cotg ⍺ =
b
c
cateto adjacente a ⍺
=
1
tg ⍺

13. Prof. Jorge
Seno, co-seno e tangente de
ângulos complementares

14. Prof. Jorge
β
Ângulos complementares
A
B
C
5
4
3
⍺ + β = 90º
⍺
tg ⍺ =
3
4
⇒
Os ângulos ⍺ e β são
complementares
sen ⍺ =
3
5
cos ⍺ =
4
5
tg β =
4
3
sen β =
4
5
cos β =
3
5

15. Prof. Jorge
β
Ângulos complementares
A
B
C
a
b
c
⍺ + β = 90º
⍺
tg ⍺ =
1
tg β
⇒
Os ângulos ⍺ e β são
complementares
sen ⍺ = cos β cos ⍺ = sen β
sec ⍺ = cosec β cosec ⍺ = sec β cotg ⍺ = tg β

16. Prof. Jorge
1 cm
2 cm
t
Exemplo
 No triângulo retângulo da figura, temos:
I. sen t = ½ II. sec t =
√5
2
III. tg t = 2
A(s) afirmativa(s) verdadeira(s) é(são):
a) I b) II c) III d) II e III e) I, II e III

17. Prof. Jorge
Seno, co-seno e tangente
de 30º, 45º e 60º.

18. Prof. Jorge
Seno, co-seno e tangente de 30º, 45º e 60º.
1tg
½cos
½sen
60º45º30º
√2/2
√2/2
√3/2
√3/2
√3/3 √3

19. Prof. Jorge
Exemplos
 A partir dos dados apresentados na figura,
determinar as medidas indicadas por x e y.
x
16
y
30º
sen 30º =
x
12
12 cm
⇒ x = 12 . 1/2 ⇒ x = 6 cm
cos 30º =
y
12
⇒ x = 12 . √3/2 ⇒ x = 6 √3 cm

20. Prof. Jorge
Exemplos
 Os triângulos ABC e BCD da figura são retângulos
em B, sendo conhecidos os ângulos BAC = 30º e
BDC = 60º, além de AD = 2 cm. Calcular os
valores de x, y e z.
30º
AB
C
D
x
y
z 2 cm
60º

21. Prof. Jorge
Identidades
trigonométricas

22. Prof. Jorge
Identidades trigonométricas
 Ferramentas de grande aplicabilidade sendo
utilizadas para:
 Obter uma razão trigonométrica, para um dado
ângulo, a partir de outra razão cujo valor seja
conhecido.
 Simplificar expressões extensas envolvendo várias
relações trigonométricas para um mesmo ângulo.

23. Prof. Jorge
Identidades trigonométricas
 A partir do triângulo retângulo abaixo vamos
deduzir algumas dessas relações.
β
A
C
B
a
c
b
⍺
b2
+ c2
= a2 (: a2
)
b2
a2
+
c2
a2
=
a2
a2
b
a
+
c
a
= 1
2 2
sen
⍺
+ cos ⍺ = 1
2 2
⇒ sen2
x + cos2
x = 1

24. Prof. Jorge
b/a
c/a
Identidades trigonométricas
 A partir do triângulo retângulo abaixo vamos
deduzir algumas dessas relações.
β
A
C
B
a
c
b
⍺
sen ⍺
cos ⍺
= =
b
a
.
a
c
=
b
c
= tg ⍺
tg x =
sen x
cos x

25. Prof. Jorge
c/a
b/a
Identidades trigonométricas
 A partir do triângulo retângulo abaixo vamos
deduzir algumas dessas relações.
β
A
C
B
a
c
b
⍺
cos ⍺
sen ⍺
= =
c
a
.
a
b
=
c
b
= cotg ⍺
cotg x =
cos x
sen x

26. Prof. Jorge
Identidades trigonométricas - Resumo
1) sen2
x + cos2
x = 1  Relação fundamental
2) tg x =
sen x
cos x
3) cotg x =
cos x
sen x
 (cos x ≠ 0)
 (sen x ≠ 0)=
1
tg x
4) sec x =
1
cos x
5) cosec x =
1
sen x
 (cos x ≠ 0)
 (sen x ≠ 0)

27. Prof. Jorge
Exemplos
 Demonstre que sec2
x = 1 + tg2
x.
sec x =
1
cos x
⇒ sec2
x =
1
cos2
x
⇒ sec2
x =
sen2
x + cos2
x
cos2
x
⇒ sec2
x =
sen2
x
cos2
x
+
cos2
x
cos2
x
⇒ sec2
x = tg2
x + 1

28. Prof. Jorge
Exemplos
 Demonstre que cosec2
x = 1 + cotg2
x.
cosec x =
1
sen x
⇒ cosec2
x =
1
sen2
x
⇒ cosec2
x =
sen2
x + cos2
x
sen2
x
⇒ cosec2
x =
sen2
x
sen2
x
+
cos2
x
sen2
x
⇒ sec2
x = 1 + cotg2
x

29. Prof. Jorge
Exemplos
 Sabendo-se que o seno de um ângulo agudo é
igual a 3/5, determine o co-seno, tangente, co-
tangente, secante e a co-secante desse ângulo.
sen2
x + cos2
x
⇒ 3
5
+
2
cos2
x = 1
⇒ 9
25
+ cos2
x = 1
⇒
9
25
–cos2
x = 1 =
25 – 9
25
⇒ cos x =
=
16
25
± 4/5 ⇒ cos x = 4/5

30. Prof. Jorge
Exemplos
 Sabendo-se que o seno de um ângulo agudo é
igual a 3/5, determine o co-seno, tangente, co-
tangente, secante e a co-secante desse ângulo.
tg x =
sen x
cos x
=
3
5
4
5
=
3
4
cotg x =
1
tg x
=
1
3
4
=
4
3

31. Prof. Jorge
Exemplos
 Sabendo-se que o seno de um ângulo agudo é
igual a 3/5, determine o co-seno, tangente, co-
tangente, secante e a co-secante desse ângulo.
sec x =
1
cos x
=
1
4
5
=
5
4
cosec x =
1
sen x
=
1
3
5
=
5
3

32. Prof. Jorge
Exemplos
 Simplificar as expressões:
a) E1 = tg x + cotg x – sec x . cosec x
b) E2 =
cotg x . sec x
cosec2
x
E1 = tg x + cotg x – sec x . cosec x
E1 =
sen x
cos x
+
cos x
sen x
–
1
cos x
1
sen x
.
E1 =
sen2
x
sen x . cos x
+ cos2
x – 1
=
sen x . cos x
1 – 1
= 0

33. Prof. Jorge
cos x
sen x
1
cos x
1
sen2
x
Exemplos
 Simplificar as expressões:
a) E1 = tg x + cotg x – sec x . cosec x
b) E2 =
cotg x . sec x
cosec2
x
E2 =
cotg x . sec x
cosec2
x
=
.
=
1
sen x
1
sen2
x
E2 =
1
sen x
. sen2
x
1
= sen x

34. Prof. Jorge
Ângulos e arcos na
circunferência

35. Prof. Jorge
O
Circunferência
A
B
C
D
E
P
r
r
r
r
r
r

36. Prof. Jorge
Elementos
B
A
BA
O O
Corda AB Diâmetro AB

37. Prof. Jorge
Elementos
A
B
Arco AB
Arco BA

38. Prof. Jorge
Arcos e ângulos
A B≡ A B≡
arco completo arco nulo

39. Prof. Jorge
Arcos e ângulos
AB
Arco de meia volta
O
Arco AB
Arco BA

40. Prof. Jorge
Arco e ângulo central
A
B
O
C
α
D
E F
γ
β
 m(AB) = ⍺
 m(CD) = β
 m(EF) = γ

41. Prof. Jorge
0o
10o
20o
30o
40o
50o
60o
70o
80o90o
100o
110o
120o
130o
140o
150o
160o
170o
180o
190o
200o
210o
220o
230o
240o
250o
260o
270o 280o 290o
300o
310o
320o
330o
340o
350o
O grau como unidade de medida

42. Prof. Jorge
0o
10o
20o
30o
40o
50o
60o
70o
80o90o
100o
110o
120o
130o
140o
150o
160o
170o
180o
190o
200o
210o
220o
230o
240o
250o
260o
270o 280o 290o
300o
310o
320o
330o
340o
350o
O grau como unidade de medida

43. Prof. Jorge
0o
10o
20o
30o
40o
50o
60o
70o
80o90o
100o
110o
120o
130o
140o
150o
160o
170o
180o
190o
200o
210o
220o
230o
240o
250o
260o
270o 280o 290o
300o
310o
320o
330o
340o
350o
1o
1º =
360
1
O grau como unidade de medida

44. Prof. Jorge
Exemplos
 Na figura, os pontos A, B, C, D, E e F dividem a
circunferência em seis arcos congruentes.
Calcular, em graus, as medidas dos arcos AB e CE
e dos ângulos centrais correspondentes.
A
B
O
C
α
D
E F
β
AB =
360º
6
= 60º
CE = 2 . 60º = 120º
⍺ = 60º e β = 120º

45. Prof. Jorge
Exemplos
 A circunferência da figura tem 12 m de raio.
Supondo que o arco AB mede 2π m, calcular em
graus, a medida do arco e do ângulo central
correspondente.
A
B
O α 2π m
12 m
Arco
(em graus)
2π m
⍺ =
360 . 2π
24
Arco
(em metros)
360º 24π m
⍺
= 30ºC = 2πr
C = 2.π.12
C = 24π

46. Prof. Jorge
O radiano como unidade de medida
A
R
O R
α
R
B
Comprimento do arco (AB) = R
⇓
m(AB) = 1 radiano
⇓
α = m(AB) = 1 rad

47. Prof. Jorge
Exemplo
A
R
O R
α
1,5R
B
Comprimento do arco (AB) = 1,5 R
⇓
m(AB) = 1,5 rad
⇓
α = m(AB) = 1,5 rad
α = m(AB) =
comprimento
R

48. Prof. Jorge
Arco completo
α =
comprimento
R
α =
2πR
R
R
A B≡
O
α
α = 2π rad

49. Prof. Jorge
9
cm
Exemplos
B
10,8 cm
 A circunferência da figura tem raio igual a 9 cm e o
comprimento do arco AB assinalado é 10,8 cm.
Calcular, em radianos, a medida de AB.
O
A
α =
comprimento
R
α =
10,8 cm
9 cm
= 1,2 rad

50. Prof. Jorge
4 cm
Exemplos
B
30º
 O arco AB da figura tem medida de 30º e o raio da
circunferência é de 4 cm. Calcular, em cm, o
comprimento do arco AB.
O
A
ângulo
x
x =
2 π.4.30
360
comprimento
360º 2π R
30º
2 π
3
= ≈ 2, 1 cm

51. Prof. Jorge
R
Exemplos
B
40 cm
 Numa circunferência, o comprimento de um arco é
de 40 cm. Esse mesmo arco mede 5 rad. Calcular a
medida do raio da circunferência.
O
A
R
α =
comprimento
R
5 =
40 cm
R
5R = 40
α
⇒ R = 8 cm

52. Prof. Jorge
Arcos especiais
00o
Arco nulo
π/290º
Arco de ¼ de
volta
π180º
Arco de
meia-volta
2π360º
Arco
completo
Medida em
radianos
Medida
em graus
Represen-
tação
O
O
O
O

53. Prof. Jorge
Transformando unidades
As medidas de um arco em graus e radianos são
proporcionais. Por isso podemos transformar uma
unidade em outra por uma regra de três.
180º correspondem a π rad

54. Prof. Jorge
2
π5
Exemplos
 Transformar 72º em radianos.
180º π rad
72º x
x =
72 .
π180
= rad

55. Prof. Jorge
5.180
Exemplos
 Exprimir rad em graus.
π rad equivale a 180º.
x =
4
=
5π
4
225º
5.π
4
=