Baixado 81 vezes
Carregado porErenilson Marinho
Trigonometria triangulo retangulo
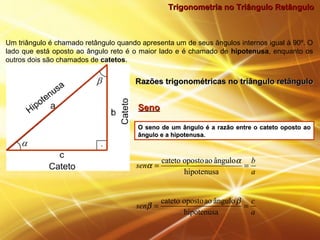
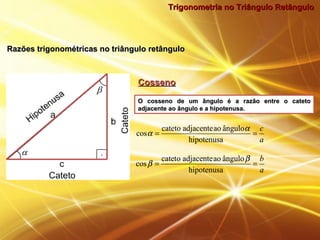
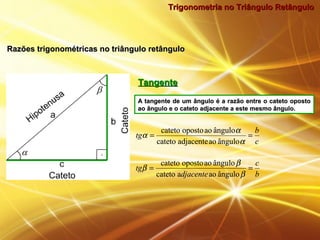
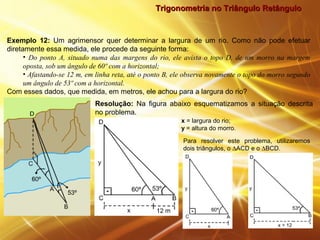
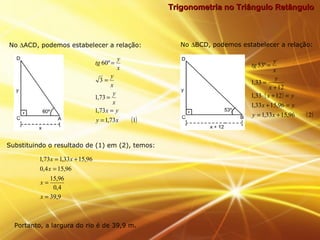
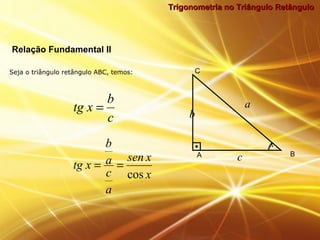
O documento discute trigonometria no triângulo retângulo, definindo seno, cosseno e tangente em termos das razões entre os catetos e a hipotenusa. Ele também apresenta exemplos numéricos ilustrando o uso destas definições para calcular medidas desconhecidas em problemas envolvendo triângulos retângulos.
Mais conteúdo relacionado
Semelhante a Trigonometria triangulo retangulo
Trigonometria triangulo retangulo
- 1. Matemática - TrigonometriaMatemática- Trigonometria Trigonometria no Triângulo Retângulo.Trigonometria no Triângulo Retângulo.
- 2. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Um triângulo é chamado retângulo quando apresenta um de seus ângulos internos igual à 90º. O lado que está oposto ao ângulo reto é o maior lado e é chamado de hipotenusa, enquanto os outros dois são chamados de catetos. Razões trigonométricas no triângulo retânguloRazões trigonométricas no triângulo retângulo SenoSeno O seno de um ângulo é a razão entre o cateto oposto aoO seno de um ângulo é a razão entre o cateto oposto ao ângulo e a hipotenusa.ângulo e a hipotenusa. a b sen == hipotenusa ânguloaoopostocateto α α a c sen == hipotenusa ânguloaoopostocateto β β a b sen == hipotenusa ânguloaoopostocateto α α a c sen == hipotenusa ânguloaoopostocateto β β
- 3. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo CossenoCosseno O cosseno de um ângulo é a razão entre o catetoO cosseno de um ângulo é a razão entre o cateto adjacente ao ângulo e a hipotenusa.adjacente ao ângulo e a hipotenusa. a c == hipotenusa ânguloaoadjacentecateto cos α α a b == hipotenusa ânguloaoadjacentecateto cos β β a c == hipotenusa ânguloaoadjacentecateto cos α α a b == hipotenusa ânguloaoadjacentecateto cos β β Razões trigonométricas no triângulo retânguloRazões trigonométricas no triângulo retângulo
- 4. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Razões trigonométricas no triângulo retânguloRazões trigonométricas no triângulo retângulo TangenteTangente A tangente de um ângulo é a razão entre o cateto opostoA tangente de um ângulo é a razão entre o cateto oposto ao ângulo e o cateto adjacente a este mesmo ângulo.ao ângulo e o cateto adjacente a este mesmo ângulo. c b tg == α α α ânguloaoadjacentecateto ânguloaoopostocateto b c djacente tg == β β β ânguloaoacateto ânguloaoopostocateto c b tg == α α α ânguloaoadjacentecateto ânguloaoopostocateto b c djacente tg == β β β ânguloaoacateto ânguloaoopostocateto
- 5. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Valores Notáveis Tabela dos valores trigonométricos de ângulos notáveis. x 30º 45º 60º sen x cos x tg x 2 1 2 2 2 3 2 3 2 2 2 1 3 3 1 3
- 6. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Exemplo 01: Queremos encostar uma escada de 8 m de comprimento em uma parede, de modo que ela forme um ângulo de 60º com o solo. A que distância da parede devemos apoiar a escada no solo? Resolução: Na figura abaixo esquematizamos a situação descrita no problema. Podemos perceber um triângulo retângulo de hipotenusa igual a 8 cm, um ângulo de 60º e o lado x que queremos calcular. Como o lado x representa o cateto adjacente ao ângulo de 60º, então: 4 82 82 1 8 º60cos = = = = x x x x Logo, o ponto de apoio da escada no solo deve ficar a 4 metros da parede.
- 7. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Exemplo 12: Um agrimensor quer determinar a largura de um rio. Como não pode efetuar diretamente essa medida, ele procede da seguinte forma: • Do ponto A, situado numa das margens do rio, ele avista o topo D, de um morro na margem oposta, sob um ângulo de 60º com a horizontal; • Afastando-se 12 m, em linha reta, até o ponto B, ele observa novamente o topo do morro segundo um ângulo de 53º com a horizontal. Com esses dados, que medida, em metros, ele achou para a largura do rio? Resolução: Na figura abaixo esquematizamos a situação descrita no problema. x = largura do rio; y = altura do morro. Para resolver este problema, utilizaremos dois triângulos, o ∆ACD e o ∆BCD.
- 8. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo ( )173,1 73,1 73,1 3 º60 xy yx x y x y x y tg = = = = = ( ) ( )296,1533,1 96,1533,1 1233,1 12 33,1 º53 += =+ =+⋅ + = = xy yx yx x y x y tg 9,39 4,0 96,15 96,154,0 96,1533,173,1 = = = += x x x xx No ∆ACD, podemos estabelecer a relação: No ∆BCD, podemos estabelecer a relação: Substituindo o resultado de (1) em (2), temos: Portanto, a largura do rio é de 39,9 m.
- 9. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Seja o triângulo retângulo ABC, sabemos pelo Teorema de Pitágoras que: Relação Fundamental I 222 acb =+ 1cos 1 1 22 22 2 2 2 2 2 2 2 22 =+ = + =+ = + xxsen a c a b a c a b a a a cb b A B C x a c
- 10. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Seja o triângulo retângulo ABC, temos: Relação Fundamental II c b xtg = x xsen a c a b xtg cos == b A B C x a c
- 11. Trigonometria no TriânguloRetânguloTrigonometria no Triângulo Retângulo Seja o triângulo retângulo ABC, temos: Ângulos Complementares βα β α cos cos =⇒ = = sen a b a b sen αβ βα −= =+ º90 º90 b A B C α a c β Assim, ( ) ( )αααα −=−= º90cosº90cos senousen Podemos perceber, também, que: ( )αβ α β α − ==⇒ = = º90 11 tgtg tg b c tg c b tg ou ( ) 1º90 =−⋅ αα tgtg