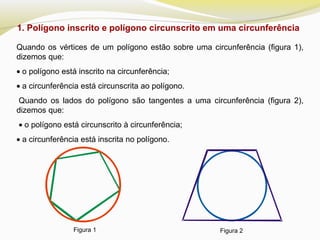
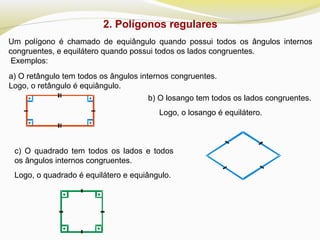
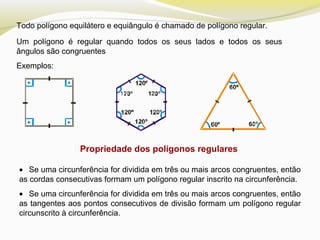
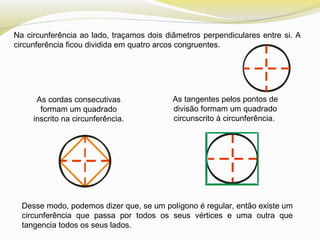
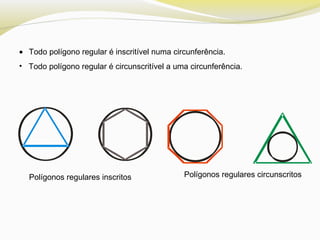
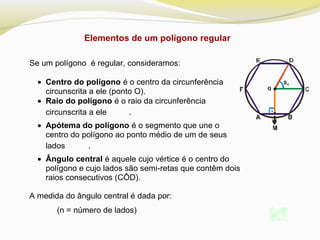
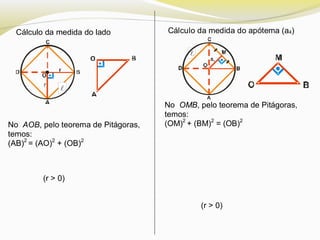
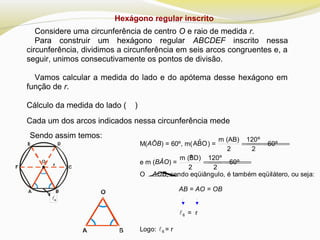
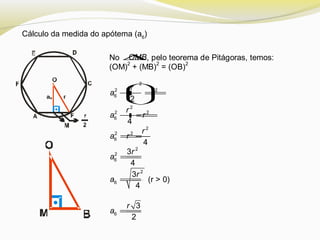
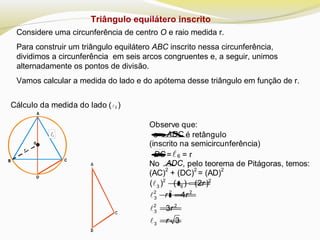
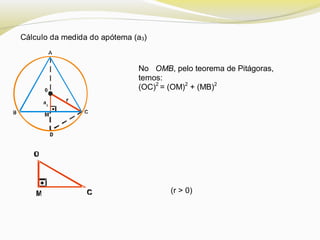
O documento discute polígonos regulares, definindo-os como polígonos equiláteros e equiângulos. Ele explica que polígonos regulares podem ser inscritos ou circunscritos em uma circunferência e fornece fórmulas para calcular o lado e a apótema de polígonos regulares como quadrados, hexágonos e triângulos equiláteros em termos do raio da circunferência.

1. Polígonos RegularesPolígonos Regulares

2. Figura 1 Figura 2
1. Polígono inscrito e polígono circunscrito em uma circunferência
Quando os vértices de um polígono estão sobre uma circunferência (figura 1),
dizemos que:
• o polígono está inscrito na circunferência;
• a circunferência está circunscrita ao polígono.
Quando os lados do polígono são tangentes a uma circunferência (figura 2),
dizemos que:
• o polígono está circunscrito à circunferência;
• a circunferência está inscrita no polígono.

3. 2. Polígonos regulares
Um polígono é chamado de equiângulo quando possui todos os ângulos internos
congruentes, e equilátero quando possui todos os lados congruentes.
Exemplos:
a) O retângulo tem todos os ângulos internos congruentes.
Logo, o retângulo é equiângulo.
b) O losango tem todos os lados congruentes.
Logo, o losango é equilátero.
c) O quadrado tem todos os lados e todos
os ângulos internos congruentes.
Logo, o quadrado é equilátero e equiângulo.

4. Todo polígono equilátero e equiângulo é chamado de polígono regular.
Um polígono é regular quando todos os seus lados e todos os seus
ângulos são congruentes
Exemplos:
Propriedade dos polígonos regulares
• Se uma circunferência for dividida em três ou mais arcos congruentes, então
as cordas consecutivas formam um polígono regular inscrito na circunferência.
• Se uma circunferência for dividida em três ou mais arcos congruentes, então
as tangentes aos pontos consecutivos de divisão formam um polígono regular
circunscrito à circunferência.

5. Na circunferência ao lado, traçamos dois diâmetros perpendiculares entre si. A
circunferência ficou dividida em quatro arcos congruentes.
As cordas consecutivas
formam um quadrado
inscrito na circunferência.
As tangentes pelos pontos de
divisão formam um quadrado
circunscrito à circunferência.
Desse modo, podemos dizer que, se um polígono é regular, então existe um
circunferência que passa por todos os seus vértices e uma outra que
tangencia todos os seus lados.

6. • Todo polígono regular é inscritível numa circunferência.
• Todo polígono regular é circunscritível a uma circunferência.
Polígonos regulares inscritos Polígonos regulares circunscritos

7. Se um polígono é regular, consideramos:
• Centro do polígono é o centro da circunferência
circunscrita a ele (ponto O).
• Raio do polígono é o raio da circunferência
circunscrita a ele .
• Apótema do polígono é o segmento que une o
centro do polígono ao ponto médio de um de seus
lados .
• Ângulo central é aquele cujo vértice é o centro do
polígono e cujo lados são semi-retas que contêm dois
raios consecutivos (CÔD).
A medida do ângulo central é dada por:
(n = número de lados)
e
Elementos de um polígono regular

8. 3. Relações métricas nos polígonos regulares
Estudaremos a seguir como calcular a medida do lado e a medida do
apótema de um polígono regular inscrito em uma circunferência em
função da medida do raio.
Quadrado inscrito
Considere uma circunferência de centro O e raio de
medida r.
Para construir um quadrado ABCD inserido nessa
circunferência, traçamos dois diâmetros perpendiculares
entre si ( e ), determinando o vértices do quadrado.
Vamos calcular a medida do lado e do apótema desse
quadrado em função de r.

9. Cálculo da medida do lado Cálculo da medida do apótema (a4)
No AOB, pelo teorema de Pitágoras,
temos:
(AB)2
= (AO)2
+ (OB)2
(r > 0)
No OMB, pelo teorema de Pitágoras,
temos:
(OM)2
+ (BM)2
= (OB)2
(r > 0)



10. Hexágono regular inscrito
Considere uma circunferência de centro O e raio de medida r.
Para construir um hexágono regular ABCDEF inscrito nessa
circunferência, dividimos a circunferência em seis arcos congruentes e, a
seguir, unimos consecutivamente os pontos de divisão.
Vamos calcular a medida do lado e do apótema desse hexágono em
função de r.
Cálculo da medida do lado ( )
Cada um dos arcos indicados nessa circunferência mede
Sendo assim temos:

M(AÔB) = 60º, m( ˆABO) =
m (AB) 120º
60º
2 2
==
e m (BÂO) =
»m (BD) 120º
60º
2 2
==
O ∆AOB, sendo eqüiângulo, é também eqüilátero, ou seja:
AB = AO = OB
6 = r
Logo: 6 = r

11. Cálculo da medida do apótema (a6
)
No ∆OMB, pelo teorema de Pitágoras, temos:
(OM)
2
+ (MB)
2
= (OB)
2
2
2 2
6
2
r
a r

+ =

2
2 2
6
4
r
a r+=
2
2 2
6
4
r
a r=−
2
2
6
3
4
r
a =
2
6
3
4
r
a = (r > 0)
6
3
2
r
a =

12. Triângulo equilátero inscrito
Considere uma circunferência de centro O e raio medida r.
Para construir um triângulo equilátero ABC inscrito nessa circunferência,
dividimos a circunferência em seis arcos congruentes e, a seguir, unimos
alternadamente os pontos de divisão.
Vamos calcular a medida do lado e do apótema desse triângulo em função de r.
Cálculo da medida do lado ( 3 )

Observe que:
•o ∆ADC é retângulo
(inscrito na semicircunferência)
•DC =6 = r
No ∆ADC, pelo teorema de Pitágoras, temos:
(AC)
2
+ (DC)
2
= (AD)
2
2 2
3 6( ) ( ) (2 )r+= 
2 2 2
3
2 2
3
4
3
r r
r
+=
=


3 3r=

13. Cálculo da medida do apótema (a3)
No OMB, pelo teorema de Pitágoras,
temos:
(OC)2
= (OM)2
+ (MB)2
(r > 0)