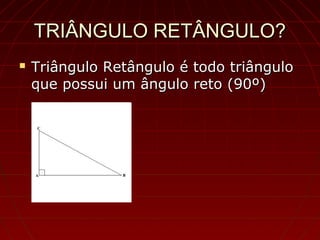
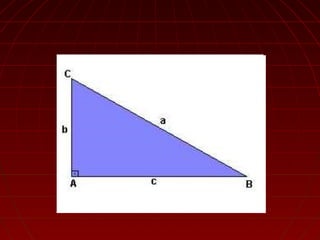
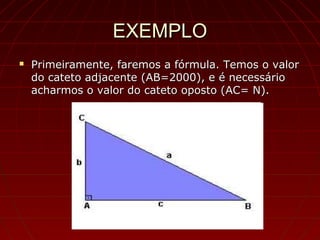
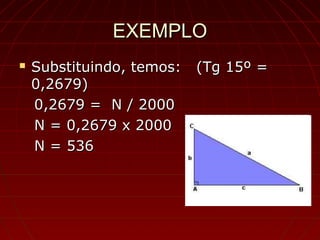
O documento explica os conceitos básicos da trigonometria, incluindo a etimologia da palavra, o que é um triângulo retângulo e seus elementos, o Teorema de Pitágoras, as razões trigonométricas, valores dos ângulos e uma demonstração de como resolver problemas usando trigonometria.

1. TRIGONOMETRIATRIGONOMETRIA

2. ETMOLOGIAETMOLOGIA
 Tri = 3Tri = 3
 Gono = ânguloGono = ângulo
 Metria = medidaMetria = medida
Ou seja, a partir da trigonometria,Ou seja, a partir da trigonometria,
“descobrimos” os valores dos“descobrimos” os valores dos
ângulos ou lados do triânguloângulos ou lados do triângulo
retângulo.retângulo.

3. TRIÂNGULO RETÂNGULO?TRIÂNGULO RETÂNGULO?
 Triângulo Retângulo é todo triânguloTriângulo Retângulo é todo triângulo
que possui um ângulo reto (90º)que possui um ângulo reto (90º)

4. ELEMENTOS DO TRIÂNGULOELEMENTOS DO TRIÂNGULO
RETÂNGULORETÂNGULO
 O triângulo retângulo é compostoO triângulo retângulo é composto
por: catetos (2 lados que formam opor: catetos (2 lados que formam o
ângulo reto) e hipotenusa (ladoângulo reto) e hipotenusa (lado
oposto ao ângulo reto e o maior ladooposto ao ângulo reto e o maior lado
do triângulo).do triângulo).

5. TEOREMA DE PITÁGORASTEOREMA DE PITÁGORAS
 O Teorema de Pitágoras é umaO Teorema de Pitágoras é uma
expressão usada quando possuímosexpressão usada quando possuímos
o valor de dois lados do triânguloo valor de dois lados do triângulo
retângulo, e precisamos saber oretângulo, e precisamos saber o
valor do terceiro lado.valor do terceiro lado.

6. TEOREMA DE PITÁGORASTEOREMA DE PITÁGORAS
 É expresso pela fórmula:É expresso pela fórmula:
(Hipotenusa) = (cateto1)² +(Hipotenusa) = (cateto1)² +
(cateto2)²(cateto2)²

7. RAZÕES TRIGONOMÉTRICASRAZÕES TRIGONOMÉTRICAS
 SENO= cateto oposto / hipotenusaSENO= cateto oposto / hipotenusa
 COSSENO = CatetoCOSSENO = Cateto
adjacente/hipotenusaadjacente/hipotenusa
 TANGENTE = cateto oposto /TANGENTE = cateto oposto /
adjacenteadjacente

8. VALORES DOS ÂNGULOSVALORES DOS ÂNGULOS
 Nos livros didáticos ou apostilas deNos livros didáticos ou apostilas de
matemática, é comum encontrarmosmatemática, é comum encontrarmos
uma tabela com o valor de cadauma tabela com o valor de cada
ângulo. Lá, encontraremos, porângulo. Lá, encontraremos, por
exemplo, que o valor da tangente deexemplo, que o valor da tangente de
45º, que é 1.45º, que é 1.

9. EXEMPLOEXEMPLO
 Suponhamos que no seguinteSuponhamos que no seguinte
triângulo ABC, o valor de AB sejatriângulo ABC, o valor de AB seja
2000, o ângulo2000, o ângulo
ABC seja 15º, e seja necessárioABC seja 15º, e seja necessário
descobrir o valor de AC. Comodescobrir o valor de AC. Como
resolveríamos este problema?resolveríamos este problema?

11. EXEMPLOEXEMPLO
 Primeiramente, faremos a fórmula. Temos o valorPrimeiramente, faremos a fórmula. Temos o valor
do cateto adjacente (AB=2000), e é necessáriodo cateto adjacente (AB=2000), e é necessário
acharmos o valor do cateto oposto (AC= N).acharmos o valor do cateto oposto (AC= N).

12. EXEMPLOEXEMPLO
 Substituindo, temos: (Tg 15º =Substituindo, temos: (Tg 15º =
0,2679)0,2679)
0,2679 = N / 20000,2679 = N / 2000
N = 0,2679 x 2000N = 0,2679 x 2000
N = 536N = 536

13. SENO E COSSENO DESENO E COSSENO DE
ÂNGULOS COMPLEMENTARESÂNGULOS COMPLEMENTARES
 Dois ângulos são complementaresDois ângulos são complementares
quando, somados, são iguais a 90º.quando, somados, são iguais a 90º.
PROPRIEDADE: o seno de ânguloPROPRIEDADE: o seno de ângulo
agudo é igual ao cosseno de seuagudo é igual ao cosseno de seu
complemento. O cosseno de umcomplemento. O cosseno de um
ângulo agudo é igual ao seno do seuângulo agudo é igual ao seno do seu
complemento.complemento.

14. SENO E COSSENO DESENO E COSSENO DE
ÂNGULOS COMPLEMENTARESÂNGULOS COMPLEMENTARES
 Sendo assim:Sendo assim:
 Sen30º Cos60º = complementares,Sen30º Cos60º = complementares,
pois somam 90ºpois somam 90º
 Sen60º=Cos30ºSen60º=Cos30º
 Cos25º=Sen65ºCos25º=Sen65º

15. Obrigado, espero que tenhamObrigado, espero que tenham
compreendido.compreendido.
 Profº.: Ronoaldo Silva CavalcanteProfº.: Ronoaldo Silva Cavalcante
 EEIEFM PEDRO POTI - Aldeia SãoEEIEFM PEDRO POTI - Aldeia São
Francisco, Baia da Traição –PBFrancisco, Baia da Traição –PB