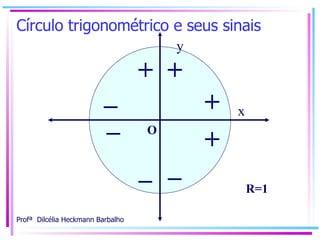
O documento fornece uma introdução à trigonometria, começando com o desenho de uma circunferência dividida em quadrantes. Explica como medir ângulos em graus e radianos e como isso está relacionado à medida da circunferência. Introduz o círculo trigonométrico e define os eixos de seno e cosseno.

1. TRIGONOMETRIA SEM MISTÉRIOS Profª Dilcélia Heckmann Barbalho

2. Trigonometria sem mistérios Oficina apresentada na semana da Matemática na Fundação Universidade Federal de Rondônia - UNIR

3. Objetivos desta oficina Desmistificar a trigonometria Reconhecer e calcular o seno , cosseno , tangente , cotangente, secante e a cosecante de qualquer ângulo dado Desenhar algumas das funções trigonométricas estudadas Reconhecer algumas das relações trigonométricas Tirar boas notas nas provas de Física...

4. Tenha em mãos Papel tamanho A4 – branco; Régua de 30 cm; Lápis ou Lapiseira (grafite); Borracha; Compasso; Calculadora (opcional).

5. Histórico Nasceu por volta de 300 aC. entre os egípcios e babilônios para solucionar problemas de distâncias e astronomia Desenvolveu-se graças aos gregos e aos indianos Atualmente, causa muita dor de cabeça aos jovens brasileiros para solucionar problemas de matemática e física...

6. Trigonos  grego – triangular metria  grego – medida Iremos estudar as medidas de triângulos, então vamos desenhar uma circunferência e inscrever nela triângulos Obteremos as medidas dos lados e dos ângulos envolvidos, ou seja, tudo o que for possível obter de um triângulo

7. Circunferência Traçar uma reta de 20cm, marcando o ponto central, origem (O) Desenhar uma circunferência com 10cm de raio, sobre a reta Encontrar a perpendicular à reta dada e que passe pelo ponto (O) O

8. Circunferência Desenhar um arco de circunferência acima e um abaixo da circunfe-rência principal. Ponta seca do compasso em A e depois em B, com abertura maior do que o raio de 10cm Traçar a perpendicular utilizando as duas intersecções dos arcos como pontos da reta O A B

9. Circunferência Assim dividimos a circunferência em quatro partes iguais Nomeamos as divisões como quadrantes Contamos as divisões seguindo a orientação convencionada, anti-horária como positiva: I, II, III e IV (primeiro, segundo, terceiro e quarto quadrantes). O I II III IV

10. Circunferência Observar que: Uma circunferência possui 360 graus (360°) e como a dividimos em quatro partes iguais, teremos em cada quadrante 90 graus: No I quadrante teremos ângulos de 0 o até 90 o no II quadrante de  90 o até 180 o e assim por diante...

11. Circunferência Observar que: O comprimento de uma circunferência é dado pela seguinte fórmula: C = 2  . R Se o raio da circunferência for R=1 (unidade) teremos que C = 2  . R  C=2  . 1  C=2  Sendo C => o arco de 360°, então 360° = C  360°= 2  e  = 180° pois  = 360°/2 Agora também podemos expressar os ângulos utilizando outra unidade de medida –– o radiano (rad), além do conhecido grau

12. Circunferência Então: 90° = 180°/2 como 180°=  teremos que  /2 = 3,14159.../2 = 1,57079...radianos 60° = 180°/3 como 180°=  teremos que  /3 = 3,14159.../3 =1,04719...radianos 45° = 180°/4 como 180°=  teremos que  /4 = 3,14159.../4 = 0,78539...radianos ...

13. Circunferência Dividimos em 2 partes, então temos 2/2 = 1 da circunferência, que vale 2  , logo: 180° = ½ . 2  =  360° = 2/2 .2  = 2  540° = 3/2 .2  = 3  ... 1/2 1/2

14. Circunferência Dividimos em 4 partes, então temos 4/4 = 1 da circunferência, a qual vale 2  : 90° = (1/4).2  =  /2 180° = (2/4).2  =  270° = (3/4).2  = 3  /2 360° = (4/4).2  = 2  360° + 90° = 450°= (5/4).2  = 5  /2 1/4 1/4 1/4 1/4

15. Circunferência Dividimos em 8 partes, então temos 8/8 = 1 da circunferência, a qual vale 2  : 45° = (1/8). 2  =  /4 90° = (2/8).2  =  /2 180° = (4/8).2  =  270° = (6/8).2  = 3  /2 360° = (4/4).2  = 2  E assim por diante... 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8

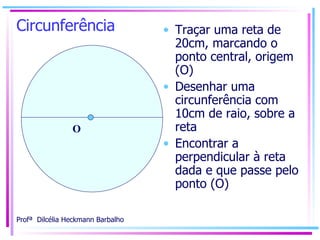
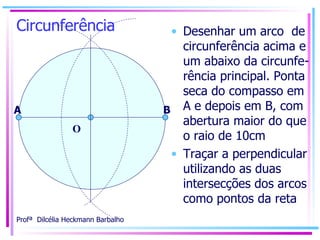
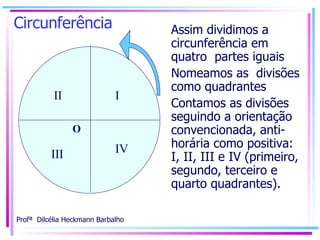
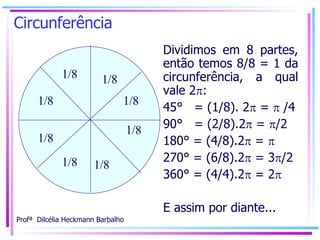
16. Circunferência  Círculo trigonométrico A circunferência passará a ser um círculo trigonométrico... R = 10cm, representará R=1 (unidade) [ 10cm equivale a 1 unidade neste círculo] Nomearemos o eixo “x” ( dentro da circunferência ) de cosseno: x = cos   = ângulo qualquer Nomearemos o eixo “y” ( dentro da circunferência ) de seno: y = sen   = ângulo qualquer

17. Círculo trigonométrico e seus sinais x y O R=1 + + + + – – – –

18. Agora já sabemos dividir a circunferência, encontrar os ângulos e transformar graus em radianos Vamos fazer uma pequena pausa para dar o próximo passo