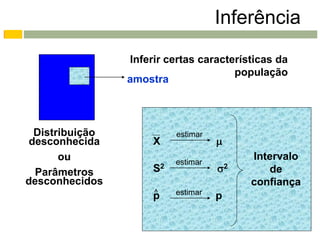
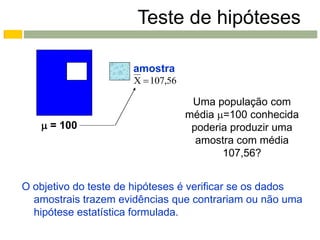
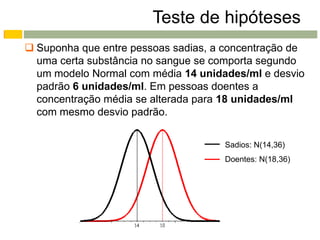
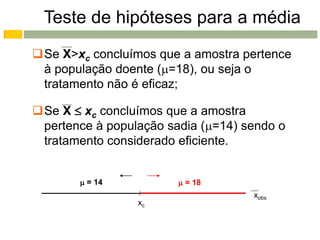
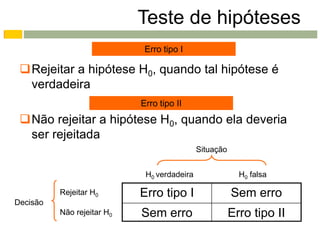
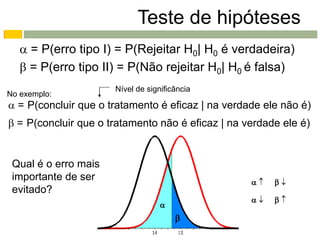
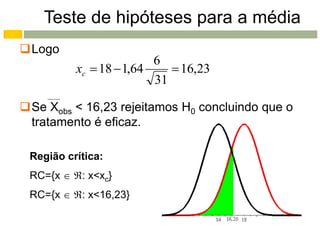
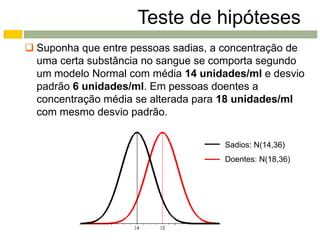
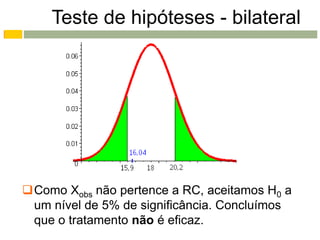
Este documento apresenta os conceitos e procedimentos básicos para a realização de testes de hipóteses unilaterais e bilaterais para a média populacional. Inicialmente, define as hipóteses nula e alternativa e discute os tipos de erros possíveis. Em seguida, explica como determinar a região crítica para os diferentes tipos de teste e como tomar a decisão final baseada na estimativa amostral e na região crítica.