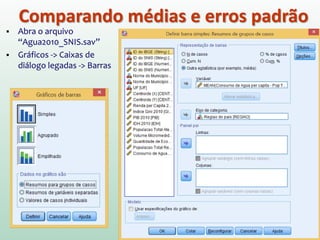
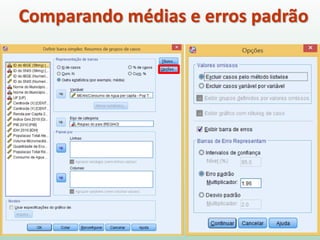
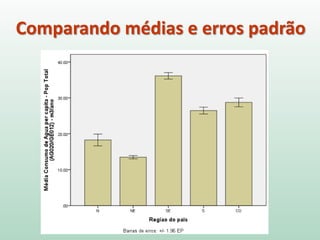
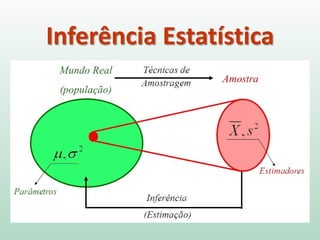
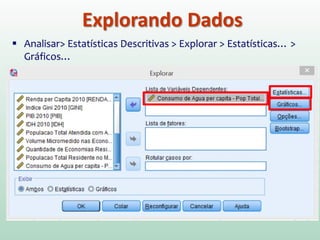
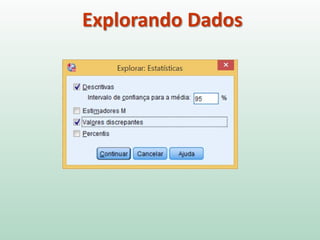
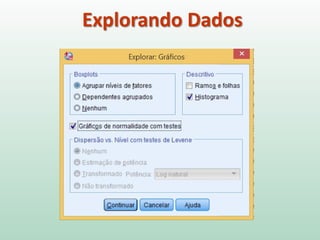
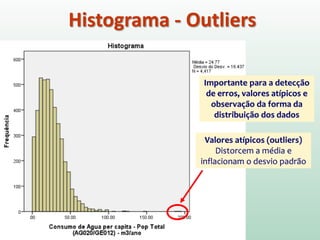
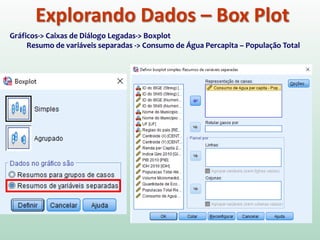
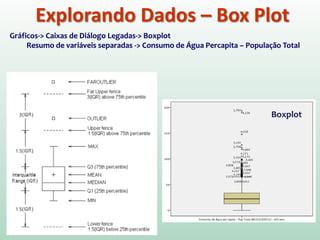
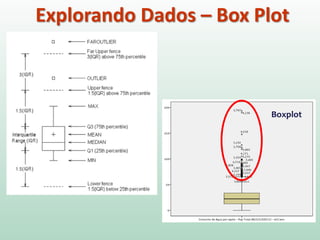
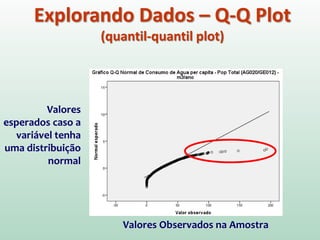
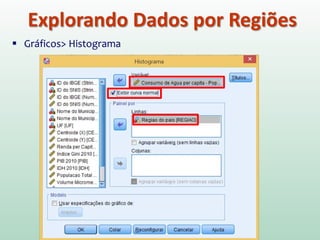
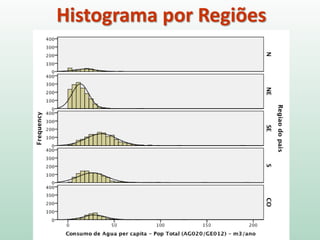
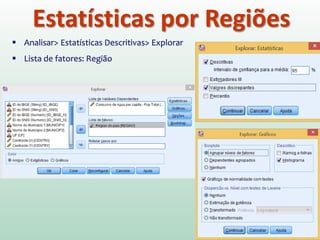
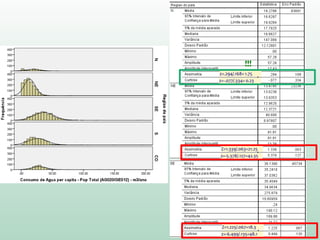
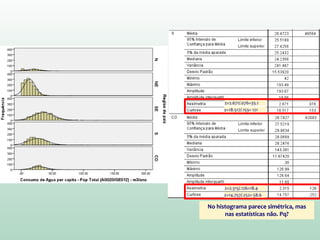
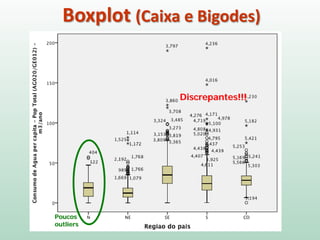
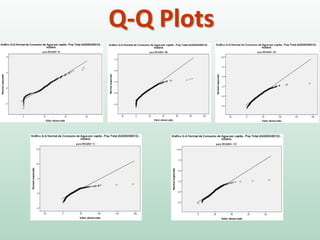
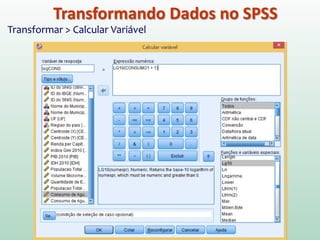
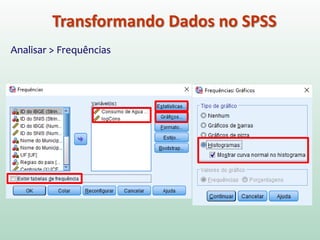
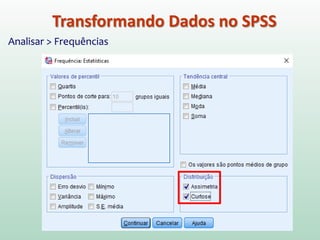
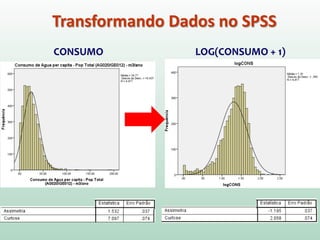
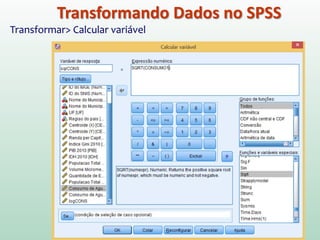
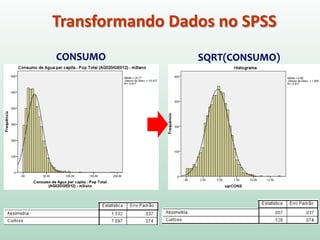
Este documento fornece instruções sobre análise exploratória de dados no SPSS, incluindo estatísticas descritivas, gráficos como caixas e bigodes e Q-Q plots, e transformações de dados para corrigir problemas de normalidade. O objetivo é explorar os dados amostrais para entender a distribuição da população e tirar conclusões estatísticas.

1. Análise Exploratória
de Dados no SPSS
Gráficos e Estatísticas Descritivas
Vitor Vieira Vasconcelos
Flávia da Fonseca Feitosa
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Junho de 2017

2. O que nós vimos na aula passada
 Distribuição Amostral
 Erro padrão da Média
 Intervalos de Confiança
 Distribuição t
 Comparação de Intervalos de Confiança (SPSS)

3. Conteúdo
 Inferência estatística
 Normalidade de dados
 Gráficos de caixas e bigodes (boxplot)
 Valores discrepantes (outliers)
 Gráficos Q-Q
 Transformações de dados

5. Leitura de Referência
Capítulo 1 – p. 47-59
Capítulo 3
Explorando Dados
(p. 85 – 124)

6. Comparando médias e erros padrão
 Abra o arquivo
“Agua2010_SNIS.sav”
 Gráficos -> Caixas de
diálogo legadas -> Barras

7. Comparando médias e erros padrão

8. Comparando médias e erros padrão

9. Comparando médias e erros padrão

10. Método científico para tirar conclusões sobre os
parâmetros da população a partir da coleta,
tratamento e análise dos dados de uma amostra
recolhida dessa população.
Inferência Estatística

11. Inferência Estatística

12. PARAMÉTRICA: Admite que a distribuição da
população tem uma forma matemática
conhecida, embora contendo um ou mais
parâmetros desconhecidos.
NÃO-PARAMÉTRICA: Pretende-se conhecer a
forma da distribuição
Inferência Estatística

13. PARAMÉTRICA: Admite que a distribuição da
população tem uma forma matemática
conhecida, embora contendo um ou mais
parâmetros desconhecidos.
Inferência Estatística
Em muitos casos, uma distribuição normal.

14. Normalidade dos Dados
Assume-se que os dados foram obtidos de uma ou
mais populações normais.
Pesquisadores verificam suas amostras
(histograma e outros testes) e se a amostra
assemelha-se a uma normal, assume-se que a
população também o é.

15. Explorando Dados no SPSS
1. Distribuição dos Escores e Valores Atípicos
(verificação da normalidade dos dados)
2. Corrigindo problemas nos dados
3. Transformando dados

16. Explorando Dados
 Analisar> Estatísticas Descritivas > Explorar > Estatísticas… >
Gráficos…

17. Explorando Dados

18. Explorando Dados

19. Explorando Dados
Positivamente assimétrica
Leptocúrtica
A Distribuição é Normal?
Converter assimetria e curtose em
escores-z
Uma distribuição normal deverá ter
assimetria e curtose nulas. Será possível que a distribuição
da população assemelhe-se a uma normal?

20. Explorando Dados
Positivamente assimétrica
Leptocúrtica
A Distribuição é Normal?
zs=(1.532-0)/0.037=41.4
zk=(7.097-0)/0.074=95.9
Curtose e
Assimetria
Significativa
Converter assimetria e curtose em
escores-z
Uma distribuição normal deverá ter
assimetria e curtose nulas. Será possível que a distribuição
da população assemelhe-se a uma normal?

21. Histograma - Outliers
Valores atípicos (outliers)
Distorcem a média e
inflacionam o desvio padrão
Importante para a detecção
de erros, valores atípicos e
observação da forma da
distribuição dos dados

22. Diagrama de Caixas e Bigodes
(boxplot)

23. Explorando Dados – Box Plot
Gráficos-> Caixas de Diálogo Legadas-> Boxplot
Resumo de variáveis separadas -> Consumo de Água Percapita – População Total

24. Explorando Dados – Box Plot
Boxplot
Gráficos-> Caixas de Diálogo Legadas-> Boxplot
Resumo de variáveis separadas -> Consumo de Água Percapita – População Total

25. Explorando Dados – Box Plot
Boxplot

27. Outliers – Valores Discrepantes

28. Explorando Dados – Q-Q Plot
(quantil-quantil plot)
Valores Observados na Amostra
Valores
esperados caso a
variável tenha
uma distribuição
normal

29. Explorando Dados por Regiões
 Gráficos> Histograma

30. Histograma por Regiões

31. Estatísticas por Regiões
 Analisar> Estatísticas Descritivas> Explorar
 Lista de fatores: Região

32. z=.294/.168= 1.75
z=-.077/.334= 0.23
Z=1.339/.063=21.25
z=-5.378/.127=42.35
Z=1.225/.067=18.3
z=-6.499/.135=48.1
!!!

33. z=2.671/.076=35.1
z=18.517/.153= 121
z=2.315/.126=18.4
z=14.757/.252= 58.6
No histograma parece simétrica, mas
nas estatísticas não. Pq?

34. Boxplot (Caixa e Bigodes)
Discrepantes!!!
Poucos
outliers

35. Q-Q Plots

36. CORRIGINDO PROBLEMAS NOS
DADOS

37. Observou algum erro de digitação
que gostaria de corrigir?
 Vá para o editor de dados, em “ir para o caso”
 Edite o valor desejado

38. Reduzindo o Impacto de Outliers
1. Remover o caso
Só deve ser feito se tiver uma boa razão para acreditar que esse
valor não é representante da população.
2. Transformar os dados
Deverá ser feito no caso de termos uma distribuição não normal.
Costumam reduzir o impacto de outliers.
3. Substituir o valor
 O próximo escore mais alto adicionado de 1
 Inverter o valor do escore-z (adicionar o triplo do desvio
padrão à média e substituir o valor atípico por esse)
 A média mais dois desvios padrão (variação do método acima)

39. Transformação dos Dados
Para corrigir problemas relacionados à não-normalidade da
distribuição ou valores atípicos (outliers)
a. Transformação logaritmica (log(Xi))
Tomar o logaritmo de um conjunto de números “esmaga” a cauda direita da
distribuição. É uma boa maneira de reduzir uma assimetria positiva.
Atenção: Não podemos obter logaritmo de zero ou valores negativos. Se tiver
zero nos dados, faça log(Xi+1)

40. Transformação dos Dados
Para corrigir problemas relacionados à não-normalidade da
distribuição ou valores atípicos (outliers)
b. Transformação por radiciação (sqr(Xi))
Tomar a raiz quadrada de valores grandes tem efeito maior do que extrair a
raiz de efeitos pequenos. Útil para dados com assimetria positiva.
Problemas com números negativos.
Somar um valor aos elementos (X + a) para não ter mais números negativos.
c. Transformação recíproca (1/Xi)
Dividir 1 por cada escore reduz o impacto dos grandes valores. A variável
transformada terá um limite inferior de zero (grandes valores ficarão
próximos de zero.
Atenção: Este tipo de transformação reverte os escores (valores grandes se
tornarão pequenos e vice-versa)
Para desinverter, utilizar a fómula: 1/(Xmáximo – X)

41. Transformando Dados no SPSS
Transformar > Calcular Variável

42. Transformando Dados no SPSS
Analisar > Frequências

43. Transformando Dados no SPSS
Analisar > Frequências

44. Transformando Dados no SPSS
CONSUMO LOG(CONSUMO + 1)

45. Transformando Dados no SPSS
Transformar> Calcular variável

46. Transformando Dados no SPSS
CONSUMO SQRT(CONSUMO)

47. Transformando Dados no SPSS
Vocês podem usar o comando “Transformar >
Calcular Variável” para realizar as mais
diversas transformações nos dados!
Por exemplo: Normalizar os dados, calcular
taxas e proporções, etc.

48. PARTE II
Realizar análises exploratórias sobre
os dados do trabalho do curso!!!
Para importar um arquivo .csv ou .dbf para o SPSS, vá em:
Arquivo> Abrir> Dados…
DICA: Vocês podem importar o arquivo .dbf que compõe o
arquivo vetorial (shapefile)

49. Atividade
Utilizando os dados que pretende usar no trabalho final da disciplina,
cada integrante do grupo escolherá ao menos uma variável e fará as
atividades a seguir.
a. Calcule as estatísticas descritivas de uma variável de sua escolha.
Explique cada uma delas.
b. Apresente o histograma, box-plot e Q-Q Plot. Explique.
c. Realize alguma(s) transformação(ões) em uma ou mais variáveis
selecionadas (ex: log, raiz quadrada…). Explique qual se
aproximou mais da distribuição normal.
d. Se houver grupos distintos (bairros, distritos), repita os itens (a) e
(b) para cada grupo. Compare intervalos de confiança da média
de uma variável de interesse. Há sobreposições? O que isso
significa? Interprete!
Já estamos elaborando o trabalho final da disciplina!!!