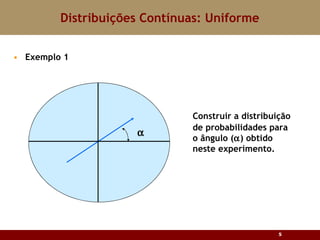
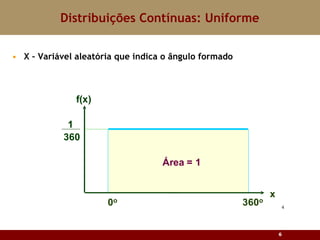
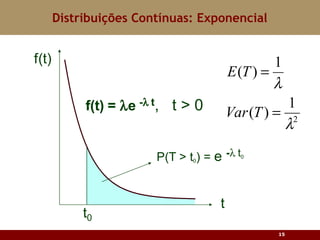
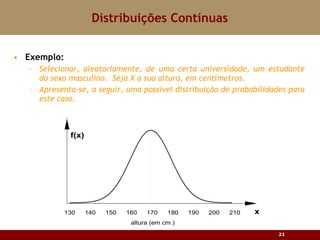
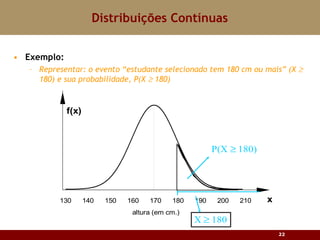
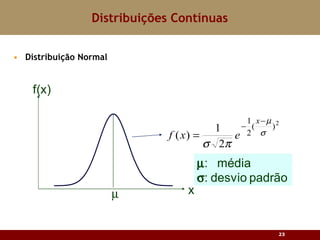
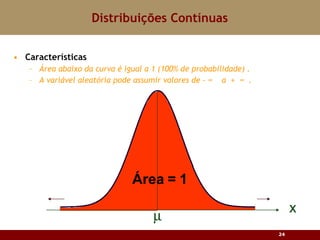
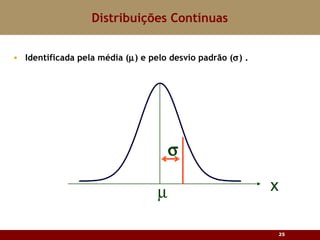
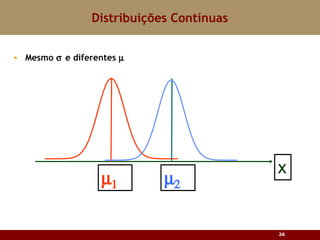
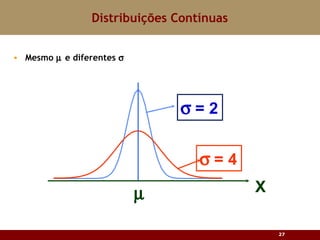
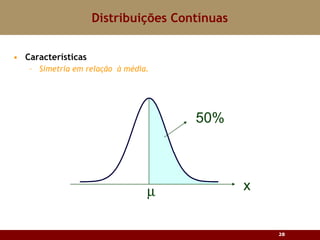
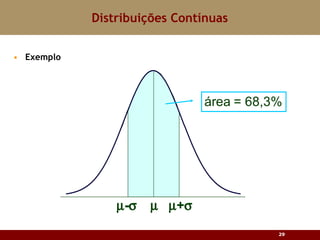
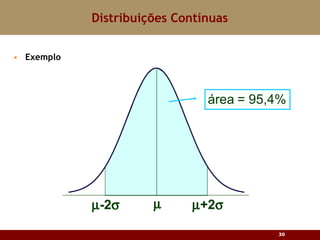
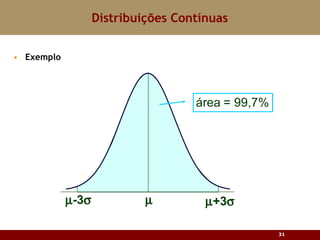
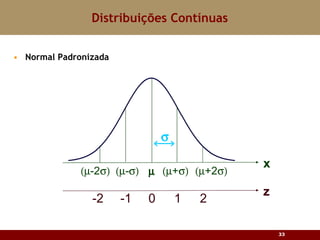
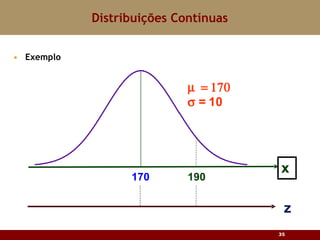
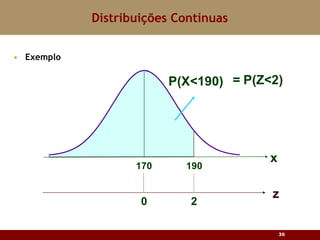
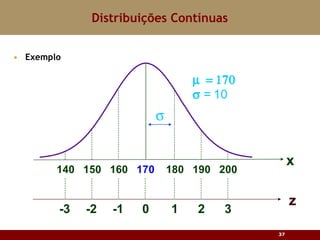
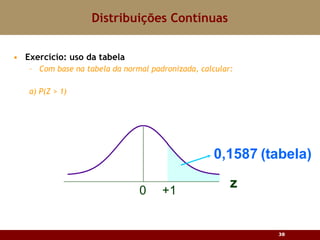
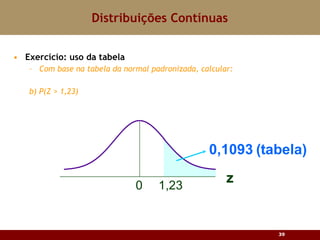
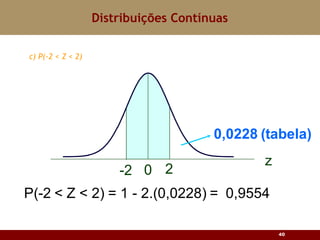
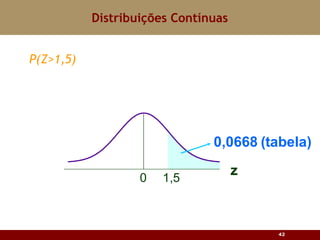
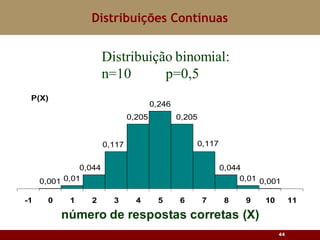
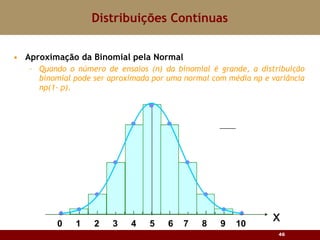
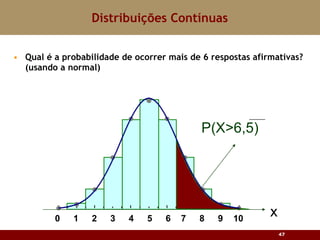
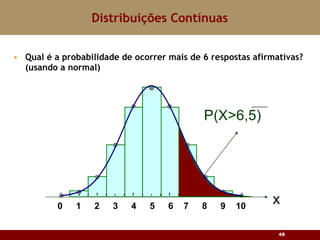
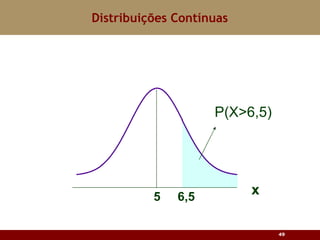
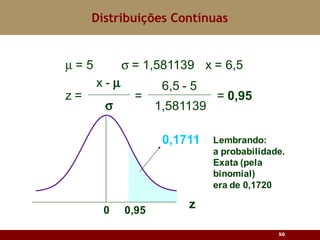
Este documento discute vários tipos de distribuições de probabilidade contínuas, incluindo uniforme, exponencial e normal. Ele fornece exemplos e explicações sobre como modelar variáveis aleatórias usando essas distribuições, calcular probabilidades e aproximar a binomial pela normal.

1. Rio de Janeiro, 04 de Abril de 2011. ESTATÍSTICA: Distribuições Contínuas Anderson Guimarães de Pinho

3. Distribuições Contínuas A distribuição de probabilidades, ou modelo probabilístico, indica, para uma variável aleatória, quais são os resultados que podem ocorrer e qual é a probabilidade de cada resultado acontecer.

9. Distribuições Contínuas: Uniforme

15. Distribuições Contínuas: Exponencial

16. Distribuições Contínuas: Exponencial

44. Distribuições Contínuas

49. Distribuições Contínuas

50. Distribuições Contínuas

51. “ Obrigado” Anderson Guimarães de Pinho “ É mais pela educação que pela instrução que se transformará a humanidade. ” Alan Kardec