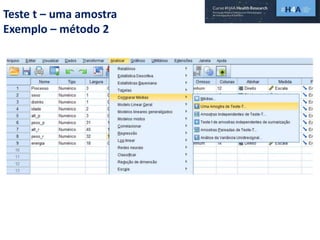
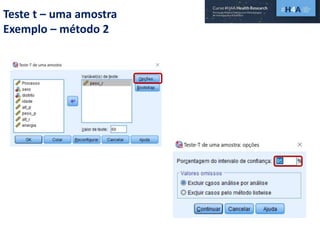
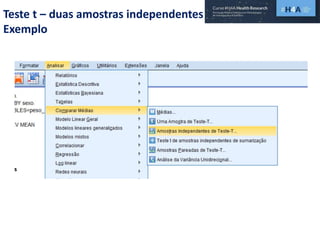
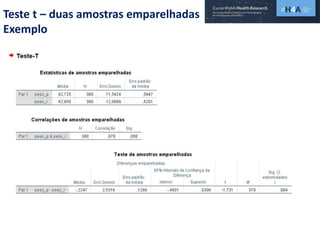
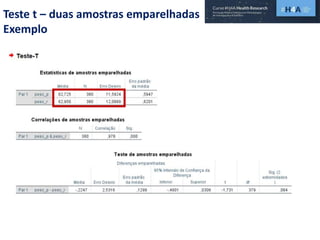
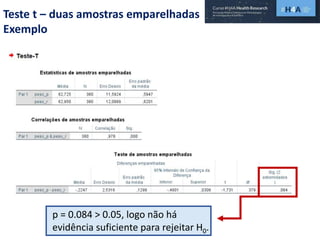
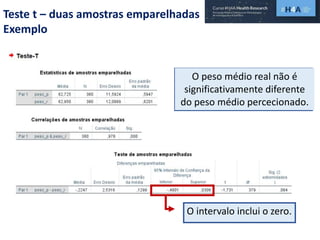
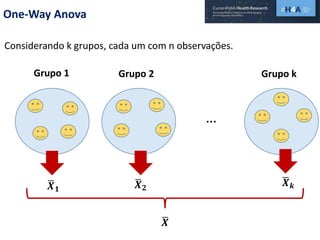
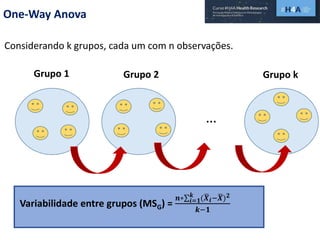
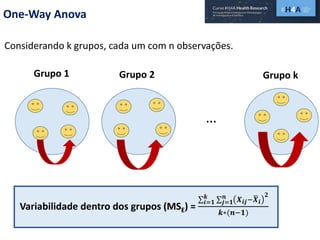
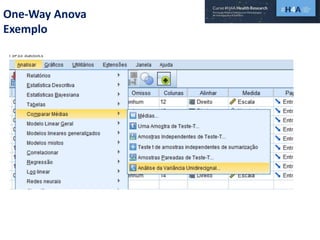
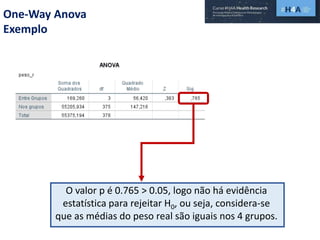
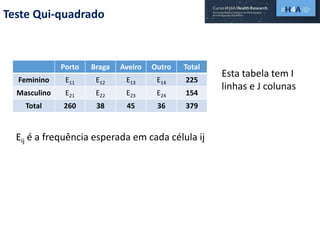
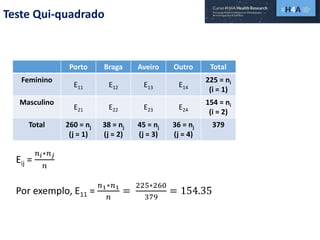
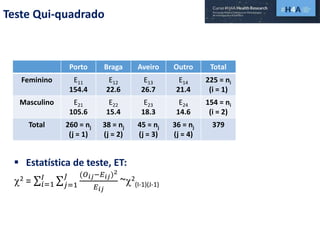
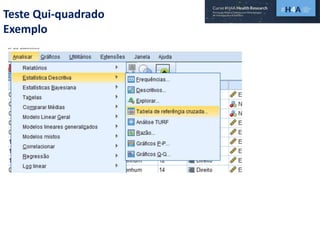
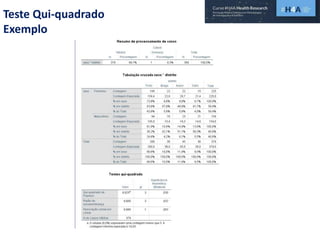
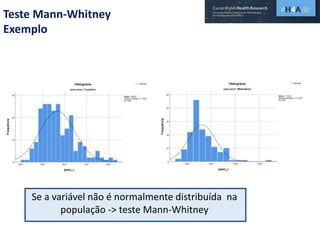
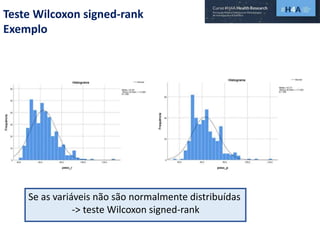
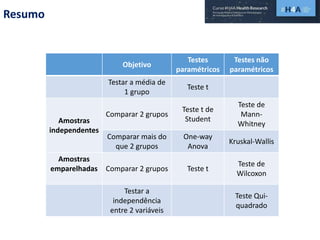
Este documento discute procedimentos estatísticos para testes de hipóteses, incluindo: 1) escolha entre testes paramétricos e não paramétricos dependendo do tamanho e distribuição das amostras; 2) formulação de hipóteses nulas e alternativas; 3) cálculo e interpretação de estatísticas de teste como o teste t. Exemplos ilustram como aplicar esses procedimentos para testar diferenças entre médias em diferentes tipos de amostras.

1. Andreia Teixeira e Carlos Martins
7 de setembro de 2019

2. Sumário
 Inferência estatística. Procedimentos a considerar na
realização dos testes.
 Hipótese nula, escolha do teste, nível de significância,
distribuição amostral e região de rejeição.
 Testes de hipóteses paramétricos para diferentes tipos de
amostras.
 Testes de hipóteses não paramétricos para diferentes tipos
de amostras.
 Exemplos e exercícios com o SPSS e interpretação de dados
em artigos científicos.

3. Inferência estatística
 Muitas vezes recolhemos uma amostra para tirar conclusões
sobre a população de onde retiramos a amostra.
 O conjunto de métodos que nos permite usar a informação da
amostra para tirar conclusões sobre a população é designado por
Inferência Estatística.
 O teorema do limite central é um resultado fundamental na
Estatística e é a base de muitos métodos de inferência.

4. Inferência estatística
Teorema do limite central:
A distribuição das médias de amostras de tamanho n, obtidas de
uma população com média  e desvio-padrão , converge para
uma distribuição normal com média  e desvio-padrão dado por
/ 𝑛.
Erro padrão da média

5. Distribuição Normal
Caraterísticas:
 Forma de “sino”.
 Simétrica em torno do valor médio.
 A média, a mediana e a moda são iguais.
 A amplitude inter-quartil é igual a 1.33*.
 A variável aleatória X tem amplitude infinita.
X~N(, 2)

6. Procedimentos a considerar na
realização dos testes
Os testes de hipóteses apresentam 5 etapas:
1. Definição de hipóteses e escolha do nível de significância.
2. Identificação da estatística de teste e respetiva distribuição.
3. Definição da regra de decisão (região de rejeição).
4. Cálculo da estatística de teste e tomada de decisão.
5. Conclusão.

7. Procedimentos a considerar na
realização dos testes
Seja X uma população com função densidade de probabilidade
f(x|θ), onde θ é um parâmetro desconhecido, sobre o qual se
pretende efetuar um teste de hipóteses.

8. Hipóteses
Seja X uma população com função densidade de probabilidade
f(x|θ), onde θ é um parâmetro desconhecido, sobre o qual se
pretende efetuar um teste de hipóteses.
Hipótese estatística: suposição relativa a um parâmetro
desconhecido da população (θ).

9. Hipóteses
Hipótese estatística: suposição relativa a um parâmetro
desconhecido da população (θ).
Teste bilateral:
H0: θ = θ0
H1: θ ≠ θ0
Teste unilateral à esquerda:
H0: θ = θ0
H1: θ < θ0
Teste unilateral à direita:
H0: θ = θ0
H1: θ > θ0

10. Tipos de erros que podem ocorrer
num teste de hipóteses
Decisão
tomada
Situação real
H0 verdadeira H1 verdadeira
Rejeitar H0 Erro tipo I Decisão
correta
Não rejeitar
H0
Decisão
correta
Erro tipo II
α = P(cometer erro tipo I) = P(Rejeitar H0|H0 é verdadeira)
β = P(cometer erro tipo II) = P(Não rejeitar H0|H1 é verdadeira)
Potência do teste, η = 1-β = P(Rejeitar H0|H1 é verdadeira)

11. Nível de significância: α
Decisão
tomada
Situação real
H0 verdadeira H1 verdadeira
Rejeitar H0 Erro tipo I = α Decisão
correta
Não rejeitar
H0
Decisão
correta
Erro tipo II
α = P(cometer erro tipo I) = P(Rejeitar H0|H0 é verdadeira)
α = 1%, 5%, 10%,…

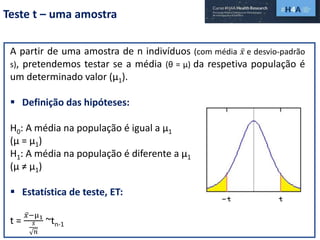
12. Região crítica, RC
Região crítica do teste: região de rejeição de H0.
Teste bilateral:
H0: θ = θ0
H1: θ ≠ θ0
RC = ]-∞, c1[ U ]c2, + ∞[
Teste unilateral à esquerda:
H0: θ = θ0
H1: θ < θ0
RC = ]-∞, c[
Teste unilateral à direita:
H0: θ = θ0
H1: θ > θ0
RC = ]c, + ∞[

13. Testes de hipóteses
Método 1
1. Formulação da hipótese nula H0 e da hipótese alternativa H1.
2. Atribuição do nível de significância α.
3. Determinação do valor crítico c e, consequentemente, da RC
para a estatística de teste sob H0.
4. Tomada de decisão com base no valor observado da estatística
de teste sob H0.

14. Testes de hipóteses
Método 2
1. Formulação da hipótese nula H0 e da hipótese alternativa H1.
2. Atribuição do nível de significância α.
3. Cálculo do valor p (p-value):
 Teste unilateral à esquerda: valor p = P(ET ≤ ETobs|H0)
 Teste unilateral à direita: valor p = P(ET ≥ ETobs|H0)
 Teste bilateral: valor p = P(|ET| ≥ |ETobs||H0)
4. Tomada de decisão:
 Se valor p < α, rejeita-se H0
 Se valor p ≥ α, não se rejeita H0

15. Testes paramétricos
Os testes paramétricos:
 exigem que a(s) amostra(s) tenha(m) distribuição normal,
especialmente se tiverem uma dimensão inferior a 30.
 em amostras de dimensão superior a 30, a distribuição aproxima-
se da distribuição normal, sendo possível aplicar os testes
paramétricos.

16. Testes paramétricos – escolha do teste
 Teste t – uma amostra
 Teste t – duas amostras independentes
 Teste t – duas amostras emparelhadas
 One-way Anova

17. Teste t – uma amostra
A partir de uma amostra de n indivíduos (com média 𝑥 e desvio-padrão
s), pretendemos testar se a média (θ = µ) da respetiva população é
um determinado valor (µ1).
 Definição das hipóteses:
H0: A média na população é igual a µ1
(µ = µ1)
H1: A média na população é diferente a µ1
(µ ≠ µ1)
 Estatística de teste, ET:
t =
𝑥−µ1
𝑠
𝑛
~tn-1

18. Teste t – uma amostra
Exemplo
 Retirou-se uma amostra de 380 pacientes de uma clínica de
nutrição X.
 Suponhamos que esta amostra é representativa dos pacientes da
clínica X. Pretende-se verificar se o peso real médio dos
pacientes é de 60 kgs.

19. Teste t – uma amostra
Exemplo
Nesta amostra, o peso real médio é
de 62.95 kgs e o desvio-padrão é de
12.09 kgs.

20. Teste t – uma amostra
Exemplo
Nesta amostra, o peso real médio é
de 62.95 kgs e o desvio-padrão é de
12.09 kgs.
 Definição das hipóteses:
H0: A média do peso real na população é 60 kgs
(µpeso_r = 60)
H1: A média do peso real na população é diferente de 60 kgs
(µpeso_r ≠ 60)
 Pressuposto: vamos assumir que a variável peso real é
normalmente distribuída.

21. Teste t – uma amostra
Exemplo
 Estatística de teste, ET:
t =
𝑥−µ1
𝑠
𝑛
=
62.95−60
12.09
380
=4.76 ~t379
 Nível de significância: α = 5%
Observação:
Neste módulo, vamos considerar sempre um nível de
significância de 5%.

22. Teste t – uma amostra
Exemplo – método 1

23. Teste t – uma amostra
Exemplo – método 1
 Definição das hipóteses:
H0: A média do peso real na população é 60 kgs
(µpeso_r = 60)
H1: A média do peso real na população é diferente de 60 kgs
(µpeso_r ≠ 60)
 Estatística de teste, ET:
t =
𝑥−µ1
𝑠
𝑛
=
62.95−60
12.09
380
=4.76 ~t379
 Nível de significância: α = 5%
-1.96 1.96
4.76

24. Teste t – uma amostra
Exemplo – método 1
Pergunta: qual a conclusão do teste de hipótese?
A) Rejeita-se H0.
B) Não se rejeita H0.

26. Teste t – uma amostra
Exemplo – método 1
Pergunta: qual a conclusão do teste de hipótese?
A) Rejeita-se H0.
B) Não se rejeita H0.
Existe evidência estatística suficiente para rejeitar H0.

27. Teste t – uma amostra
Exemplo – método 2
 Definição das hipóteses:
H0: A média do peso real na população é 60 kgs
(µpeso_r = 60)
H1: A média do peso real na população é diferente de 60 kgs
(µpeso_r ≠ 60)
 Estatística de teste, ET:
t =
𝑥−µ1
𝑠
𝑛
=
62.95−60
12.09
380
=4.76 ~t379
 Nível de significância: α = 5%
 Cálculo do valor p (SPSS):

28. Teste t – uma amostra
Exemplo – método 2

29. Teste t – uma amostra
Exemplo – método 2

30. Teste t – uma amostra
Exemplo – método 2
 Cálculo do valor p (SPSS): p < 0.001
 Interpretação do valor p (SPSS):
Como p < 0.05, há evidência suficiente para rejeitar H0.

31. Teste t – uma amostra
Exemplo – método 2
Não contém o zero!
Com 95% de confiança, é possível
dizer que o peso médio real está
entre 61.73 kgs e 64.17 kgs.

32. Teste t – duas amostras independentes
Consideremos duas amostras independentes de indivíduos, A e B,
provenientes de duas populações.
A amostra A tem n1 indivíduos, média 𝑥 𝐴 e desvio-padrão sA.
A amostra B tem n2 indivíduos, média 𝑥 𝐵 e desvio-padrão sB.
Com base nestas duas amostras, pretendemos testar se a média das
duas populações são iguais.
 Pressupostos:
- As duas amostras seguem uma distribuição normal
- Variâncias populacionais iguais

33. Teste t – duas amostras independentes
 Definição das hipóteses:
H0: µA = µB (ou µA - µB = 0)
H1: µA ≠ µB (ou µA - µB ≠ 0)
 Estatística de teste, ET:
t =
( 𝑥 𝐴− 𝑥 𝐵)−(µ 𝐴−µ 𝐵)
𝑠𝑝∗
1
𝑛 𝐴
+
1
𝑛 𝐵
~tnA+nB-2
sp é uma estimativa agrupada dos dois
desvios-padrões (sA e sB).

34. Teste t – duas amostras independentes
 Pressupostos:
As duas amostras seguem uma distribuição normal
Variâncias populacionais iguais
Teste de Levene
 Definição das hipóteses:
H0: 2
A = 2
B
H1: 2
A ≠ 2
B
Se as variâncias nos dois grupos
não forem iguais, não é possível
calcular sp e recorre-se a uma
forma modificada do teste t.
O SPSS incorpora no teste t, o
teste de Levene.

35. Teste t – duas amostras independentes
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso real médio das mulheres é igual ao dos homens.

36. Teste t – duas amostras independentes
Exemplo
Nesta amostra, o peso real médio das
mulheres é de 56.67 kgs e o desvio-
padrão é de 7.91 kgs. O peso real
médio dos homens é de 72.16 kgs e o
desvio-padrão é de 11.24 kgs.
 Definição das hipóteses:
H0: µM = µH
H1: µM ≠ µH
 Pressupostos: vamos assumer que as amostras são normalmente
distribuídas.

37. Teste t – duas amostras independentes
Exemplo

38. Teste t – duas amostras independentes
Exemplo

39. Teste t – duas amostras independentes
Exemplo
 O valor p para o teste de Levene é < 0.001. Logo, para um nível de
significância de 5%, rejeita-se a igualdade das variâncias entre os
dois grupos.

40. Teste t – duas amostras independentes
Exemplo
 O valor p para o teste t é < 0.001. Logo, para um nível de
significância de 5%, rejeita-se a igualdade das médias do peso
entre os dois grupos (homens vs mulheres).

41. Teste t – duas amostras independentes
Exemplo
Não contém o zero!
A média do peso das mulheres é
significativamente inferior à dos
homens.

42. Teste t – duas amostras emparelhadas
Consideremos duas amostras emparelhadas de indivíduos, A e B, e
suponhamos que se pretende testar se as médias populacionais dos
dois grupos são iguais.
 Pressupostos:
- As amostras seguem uma distribuição normal (ou a variável da
diferença é normalmente distribuída)
 Definição das hipóteses:
H0: µA = µB (ou µA - µB = 0)
H1: µA ≠ µB (ou µA - µB ≠ 0)
 Estatística de teste, ET:
t =
𝑚é𝑑𝑖𝑎 𝑑𝑎𝑠 𝑑𝑖𝑓𝑒𝑟𝑒𝑛ç𝑎𝑠
𝑒𝑟𝑟𝑜 𝑝𝑎𝑑𝑟ã𝑜 𝑑𝑎𝑠 𝑑𝑖𝑓𝑒𝑟𝑒𝑛ç𝑎𝑠
~tn-1

43. Teste t – duas amostras emparelhadas
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso percecionado médio é igual ao peso real médio.

44. Teste t – duas amostras emparelhadas
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso percecionado médio é igual ao peso real médio.
 Definição das hipóteses:
H0: µpeso_r = µpeso_p
H1: µpeso_r ≠ µpeso_p

45. Teste t – duas amostras emparelhadas
Exemplo

46. Teste t – duas amostras emparelhadas
Exemplo

47. Teste t – duas amostras emparelhadas
Exemplo

48. Teste t – duas amostras emparelhadas
Exemplo

49. Teste t – duas amostras emparelhadas
Exemplo
p = 0.084 > 0.05, logo não há
evidência suficiente para rejeitar H0.

50. Teste t – duas amostras emparelhadas
Exemplo
O peso médio real não é
significativamente diferente
do peso médio percecionado.
O intervalo inclui o zero.

51. One-Way Anova
Consideremos mais do que duas amostras independentes de
indivíduos e, suponhamos que se pretende testar se as médias
populacionais dos grupos são iguais.
 Pressupostos:
- As amostras seguem uma distribuição normal
- As variâncias entre os grupos são iguais (Teste de Levene)
 Definição das hipóteses:
H0: µ1 = µ2 = µ3 = … = µk
H1: Existe pelo menos um par i, j para o qual µi ≠ µj (1 ≤ i, j ≤ k)
 Estatística de teste, ET:
F =
𝑉𝑎𝑟𝑖𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒 𝑒𝑛𝑡𝑟𝑒 𝑔𝑟𝑢𝑝𝑜𝑠 (𝑀𝑆𝐺)
𝑉𝑎𝑟𝑖𝑎𝑏𝑖𝑙𝑖𝑑𝑎𝑑𝑒 𝑑𝑒𝑛𝑡𝑟𝑜 𝑑𝑜𝑠 𝑔𝑟𝑢𝑝𝑜𝑠 (𝑀𝑆𝐸)
~Fk-1, n-k

52. One-Way Anova
…
Grupo 1 Grupo 2 Grupo k
Considerando k grupos, cada um com n observações.
𝑿 𝟏 𝑿 𝟐
𝑿 𝒌
𝑿

53. One-Way Anova
…
Grupo 1 Grupo 2 Grupo k
Variabilidade entre grupos (MSG) =
𝒏∗ 𝒊=𝟏
𝒌
( 𝑿 𝒊− 𝑿) 𝟐
𝒌−𝟏
Considerando k grupos, cada um com n observações.

54. One-Way Anova
…
Grupo 1 Grupo 2 Grupo k
Variabilidade dentro dos grupos (MSE) =
𝒊=𝟏
𝒌
𝒋=𝟏
𝒏
𝑿 𝒊𝒋− 𝑿 𝒊
𝟐
𝒌∗(𝒏−𝟏)
Considerando k grupos, cada um com n observações.

55. One-Way Anova
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso real médio é igual nos diferentes distritos.

56. One-Way Anova
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso real médio é igual nos diferentes distritos.
 Definição das hipóteses:
H0: µpeso_r(Porto) = µpeso_r(Braga) = µpeso_r(Aveiro) = µpeso_r(Outro)
H1: Existe, pelo menos, um par de distritos X, Y para os quais
µpeso_r(X) ≠ µpeso_r(Y)
X, Y {Porto, Braga, Aveiro, Outro}

57. One-Way Anova
Exemplo

58. One-Way Anova
Exemplo

59. One-Way Anova
Exemplo

60. One-Way Anova
Exemplo
O valor p é 0.837 > 0.05, logo não há evidência
estatística para rejeitar H0, ou seja, considera-se
que as variâncias são iguais nos 4 grupos.

61. One-Way Anova
Exemplo

62. One-Way Anova
Exemplo
Pergunta: qual a conclusão do teste da Anova?
A) Rejeita-se H0.
B) Não se rejeita H0.

64. One-Way Anova
Exemplo
Pergunta: qual a conclusão do teste da Anova?
A) Rejeita-se H0.
B) Não se rejeita H0.

65. One-Way Anova
Exemplo
O valor p é 0.765 > 0.05, logo não há evidência
estatística para rejeitar H0, ou seja, considera-se
que as médias do peso real são iguais nos 4 grupos.

66. Verificação da assunção
da normalidade – análise visual
A verificação da assunção da normalidade pode ser realizada apenas
por análise visual do histograma da variável na amostra (ou em cada
um dos grupos em análise, se for o caso).

67. Verificação da assunção
da normalidade – testes
A verificação da assunção da normalidade pode ser realizada através
de testes:
 Kolmogorov-Smirnov (amostras de dimensão > 30)
 Shapiro-Wilk (amostras de dimensão ≤ 30)
 Definição das hipóteses:
H0: A amostra provém de uma distribuição Normal
H1: A amostra não provém de uma distribuição Normal
A utilidade destes testes é muito limitada!

68. Verificação da assunção
da normalidade – testes

69. Verificação da assunção
da normalidade – testes

70. Verificação da assunção
da normalidade – testes

71. Verificação da assunção
da normalidade – testes

72. Verificação da assunção
da normalidade – testes
O valor p < 0.001 <
0.05, logo há
evidência estatística
para rejeitar H0, ou
seja, considera-se que
a amostra não provém
de uma distribuição
normal.

73. Verificação da assunção
da normalidade – testes
O teste K-S é muito
sensível em amostras
grandes. Obtém-se
valores p significativos
para pequenos
desvios à
normalidade.

74. Testes não paramétricos
Os testes não paramétricos são utilizados quando:
 as variáveis são qualitativas com escala de medida nominal ou
ordinal.
 as variáveis são quantitativas mas não cumprem os pressupostos
dos testes paramétricos (normalidade dos dados e/ou
homogeneidade das variâncias).

75. Testes não paramétricos
 Uma vantagem dos testes não paramétricos é a simplicidade do
ponto de vista do cálculo e a aplicabilidade a pequenas amostras
(frequentes em estudos pilotos ou em estudos de doenças raras).
 A desvantagem destes testes é que não são tão potentes quanto
os testes paramétricos, ou seja, com os testes não paramétricos
não se encontram tantas diferenças entre os dados, quando
essas diferenças realmente existem.

76. Testes não paramétricos –
escolha do teste
 Teste Qui-quadrado
 Teste de Mann-Whitney
 Teste de Wilcoxon
 Teste de Kruskal-Wallis

77. Teste Qui-quadrado
É também possível construir testes de hipóteses envolvendo apenas
variáveis categóricas.
No modulo IV, a relação entre duas variáveis categóricas foi
observada através de tabelas cruzadas.

78. Teste Qui-quadrado
Relembrar…
A relação entre
a variável sexo e
a variável
distrito

79. Teste Qui-quadrado
Relembrar…
A relação entre
a variável sexo e
a variável
distrito

80. Teste Qui-quadrado
Relembrar…
A relação entre
a variável sexo e
a variável
distrito
Parece existir uma relação entre as variáveis.

81. Teste Qui-quadrado
 Definição das hipóteses:
H0: A variável sexo e a variável distrito são independentes
H1: A variável sexo e a variável distrito não são independentes

82. Teste Qui-quadrado
Porto Braga Aveiro Outro Total
Feminino O11 O12 O13 O14 225
Masculino O21 O22 O23 O24 154
Total 260 38 45 36 379
Esta tabela tem I
linhas e J colunas
Oij é a frequência observada em cada célula ij

83. Teste Qui-quadrado
Porto Braga Aveiro Outro Total
Feminino O11
166
O12
22
O13
22
O14
15
225
Masculino O21
94
O22
16
O23
23
O24
21
154
Total 260 38 45 36 379
Esta tabela tem I
linhas e J colunas
Oij é a frequência observada em cada célula ij

84. Teste Qui-quadrado
Porto Braga Aveiro Outro Total
Feminino E11 E12 E13 E14 225
Masculino E21 E22 E23 E24 154
Total 260 38 45 36 379
Esta tabela tem I
linhas e J colunas
Eij é a frequência esperada em cada célula ij

85. Teste Qui-quadrado
Porto Braga Aveiro Outro Total
Feminino
E11 E12 E13 E14
225 = ni
(i = 1)
Masculino
E21 E22 E23 E24
154 = ni
(i = 2)
Total 260 = nj
(j = 1)
38 = nj
(j = 2)
45 = nj
(j = 3)
36 = nj
(j = 4)
379
Eij =
𝑛 𝑖∗𝑛 𝑗
𝑛
Por exemplo, E11 =
𝑛1∗𝑛1
𝑛
=
225∗260
379
= 154.35

86. Teste Qui-quadrado
Porto Braga Aveiro Outro Total
Feminino E11
154.4
E12
22.6
E13
26.7
E14
21.4
225 = ni
(i = 1)
Masculino E21
105.6
E22
15.4
E23
18.3
E24
14.6
154 = ni
(i = 2)
Total 260 = nj
(j = 1)
38 = nj
(j = 2)
45 = nj
(j = 3)
36 = nj
(j = 4)
379
 Estatística de teste, ET:
2 = 𝑖=1
𝐼
𝑗=1
𝐽 (𝑂 𝑖𝑗−𝐸 𝑖𝑗)2
𝐸 𝑖𝑗
~2
(I-1)(J-1)

87. Teste Qui-quadrado
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se a
variável sexo e a variável distrito são independentes.
 Definição das hipóteses:
H0: A variável sexo e a variável distrito são independentes
H1: A variável sexo e a variável distrito não são independentes

88. Teste Qui-quadrado
Exemplo

89. Teste Qui-quadrado
Exemplo

90. Teste Qui-quadrado
Exemplo

91. Teste Qui-quadrado
Exemplo

92. Teste Qui-quadrado
Exemplo

93. Teste Qui-quadrado
Exemplo

94. Teste Qui-quadrado
Exemplo
O valor p = 0.030 <
0.05, logo há
evidência estatística
para rejeitar H0, ou
seja, considera-se que
as variáveis sexo e
distrito não são
independentes.

95. Teste Qui-quadrado
 Pressupostos:
Não existir mais do que 20% dos valores esperados menores que 5.

96. Teste Qui-quadrado
Exemplo
 Pressupostos:
Não existir mais do que 20% dos valores esperados menores que 5.
Em tabelas 2*2, se
este pressuposto não
for satisfeito -> teste
exato de Fisher.

97. Teste Mann-Whitney
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso real médio das mulheres é igual ao dos homens.

98. Teste Mann-Whitney
Exemplo

99. Teste Mann-Whitney
Exemplo

100. Teste Mann-Whitney
Exemplo
Se a variável não é normalmente distribuída na
população -> teste Mann-Whitney

101. Teste Mann-Whitney
Exemplo
 Definição das hipóteses:
H0: Não há diferenças no peso real nos dois grupos
H1: Existem diferenças no peso real nos dois grupos

102. Teste Mann-Whitney
Exemplo

103. Teste Mann-Whitney
Exemplo

104. Teste Mann-Whitney
Exemplo
Estatística de teste
O valor p < 0.001 < 0.05,
logo há evidência estatística
para rejeitar H0, ou seja,
existem diferenças no peso
real entre os homens e as
mulheres.

105. Teste Wilcoxon signed-rank
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso percecionado médio é igual ao peso real médio.

106. Teste Wilcoxon signed-rank
Exemplo

107. Teste Wilcoxon signed-rank
Exemplo

108. Teste Wilcoxon signed-rank
Exemplo
Se as variáveis não são normalmente distribuídas
-> teste Wilcoxon signed-rank

109. Teste Wilcoxon signed-rank
Exemplo
 Definição das hipóteses:
H0: Não há diferenças entre o peso real e o peso percecionado
H1: Existem diferenças entre o peso real e o peso percecionado

110. Teste Wilcoxon signed-rank
Exemplo
Pergunta: no teste t de amostras emparelhadas (teste
paramétrico) não se verificou evidência estatística para rejeitar H0.
Então, é possível concluir que o resultado do teste de Wilcoxon
será:
A) Rejeita-se H0.
B) Não se rejeita H0.
C) Nada se pode concluir.

112. Teste Wilcoxon signed-rank
Exemplo
Pergunta: no teste t de amostras emparelhadas (teste
paramétrico) não se verificou evidência estatística para rejeitar H0.
Então, é possível concluir que o resultado do teste de Wilcoxon
será:
A) Rejeita-se H0.
B) Não se rejeita H0.
C) Nada se pode concluir.

113. Teste Wilcoxon signed-rank
Exemplo

114. Teste Wilcoxon signed-rank
Exemplo

115. Teste Wilcoxon signed-rank
Exemplo
O valor p = 0.307 > 0.05, logo
não há evidência estatística
para rejeitar H0, ou seja, não
existem diferenças
significativas entre o peso real
e o peso percecionado.

116. Teste Kruskal-Wallis
Exemplo
Pretendemos verificar, nos pacientes da clínica de nutrição X, se o
peso real médio é igual nos diferentes distritos.

117. Teste Kruskal-Wallis
Exemplo

118. Teste Kruskal-Wallis
Exemplo

119. Teste Kruskal-Wallis
Exemplo

120. Teste Kruskal-Wallis
Exemplo
Se as variáveis não são normalmente distribuídas
-> teste Kruskal-Wallis
 Definição das hipóteses:
H0: Não há diferenças no peso real nos quatro grupos
H1: Existem diferenças no peso real, pelo menos, entre dois grupos

121. Teste Kruskal-Wallis
Exemplo

122. Teste Kruskal-Wallis
Exemplo

123. Teste Kruskal-Wallis
Exemplo
O valor p = 0.598 > 0.05, logo
não há evidência estatística
para rejeitar H0, ou seja, não
existem diferenças
significativas do peso real nos 4
distritos.

124. Resumo
Objetivo
Testes
paramétricos
Testes não
paramétricos
Testar a média de
1 grupo
Teste t
Amostras
independentes
Comparar 2 grupos
Teste t de
Student
Teste de
Mann-
Whitney
Comparar mais do
que 2 grupos
One-way
Anova
Kruskal-Wallis
Amostras
emparelhadas Comparar 2 grupos Teste t
Teste de
Wilcoxon
Testar a
independência
entre 2 variáveis
Teste Qui-
quadrado

125. Exemplos em publicações
Exemplo 1

126. Exemplos em publicações
Exemplo 1

127. Exemplos em publicações
Exemplo 1

128. Exemplos em publicações
Exemplo 1

129. Exemplos em publicações
Exemplo 1

130. Exemplos em publicações
Exemplo 1

131. Exemplos em publicações
Exemplo 1

132. Exemplos em publicações
Exemplo 1

133. Exemplos em publicações
Exemplo 2

134. Exemplos em publicações
Exemplo 2

135. Exemplos em publicações
Exemplo 2

136. Exemplos em publicações
Exemplo 2

137. Exemplos em publicações
Exemplo 2

138. Exemplos em publicações
Exemplo 2

139. Exemplos em publicações
Exemplo 2

140. BIBLIOGRAFIA
 “Análise Estatística com o SPSS Statistics”, J. Maroco. (2018). 7ª
Edição, ReportNumber.