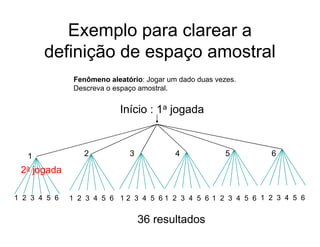
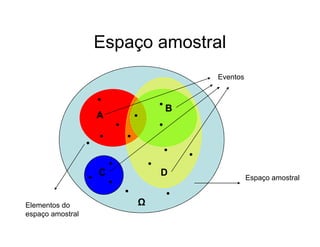
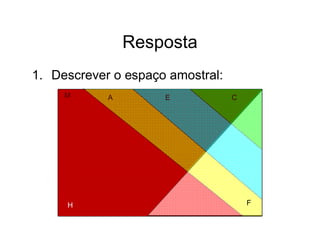
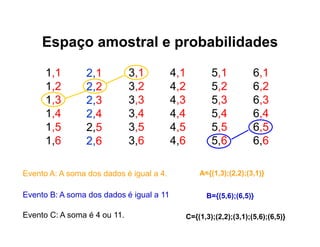
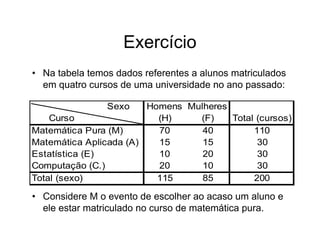
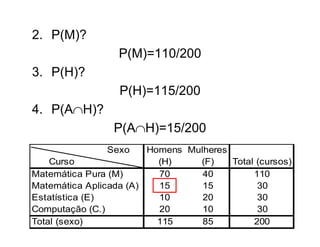
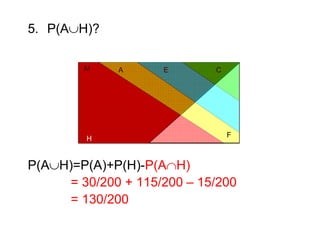
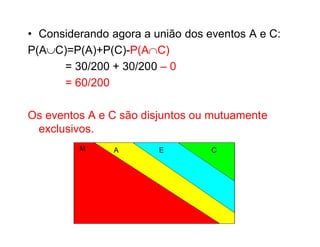
Este documento apresenta conceitos básicos de probabilidade. Em três frases, resume: 1) É introduzido o conceito de modelo probabilístico para quantificar incertezas em fenômenos aleatórios; 2) São revisados conceitos da teoria dos conjuntos como espaço amostral e eventos para definir probabilidades; 3) São apresentadas as propriedades que uma função deve satisfazer para ser considerada uma probabilidade.

1. Aula 5
Probabilidade
Profa. Dra. Juliana Garcia Cespedes
Departamento de Matemática e Computação
UNIFEI – MAT 013

2. Introdução
• Até agora vimos que a análise de um conjunto de dados
por meio de técnicas numéricas nos permite calcular
medidas de posição (média, mediana, moda) e medidas
de dispersão (variância e desvio padrão).
• Poderemos caracterizar uma massa de dados, com o
objetivo de organizar e resumir informações.
• Essas medidas são chamadas de estimativas
associadas a populações das quais os dados foram
extraídos na forma de amostras.

3. Modelos probabilísticos
• Agora estudaremos os chamados modelos probabilísticos.
• São modelos que permitem, sem a observação direta do
fenômeno aleatório, reproduzir de maneira razoável a
distribuição de frequências.
Definição: Fenômeno aleatório é a situação ou acontecimento
cujos resultados não podem ser previstos com certeza.
Ex: Condições climáticas do próximo domingo.
Taxa de inflação do próximo mês.
Em situações como estas, modelos probabilísticos podem ser
estabelecidos para quantificar as incertezas das diversas
ocorrências.

4. Conceitos da teoria dos conjuntos -
REVISÃO
• Chamamos de espaço amostral o conjunto de todos os
possíveis resultados de um certo fenômeno aleatório.
Representaremos pela letra grega Ω.
• Subconjuntos de Ω são denominados eventos e
representados por letras maíusculas (A, B, C, …).
• Um subconjunto vazio do espaço amostral é representado
por .

5. Espaço amostral
Eventos
B
A
C D Espaço amostral
Elementos do Ω
espaço amostral

6. Propriedades dos eventos
• A união de dois eventos A e B, denotada por AB
representa a ocorrência de pelo menos um dos eventos
A ou B.
• A intersecção do evento A com o B, denotada por AB,
é a ocorrência simultânea de A e B.

7. Propriedades dos eventos
• Dois eventos A e B são disjuntos ou mutuamente
exclusivos quanto não têm elementos em comum. Isto é
AB=.
• Dois eventos A e B são chamados complementares se
AB= e AB=Ω.
A B O evento B
B complementar de A
é também denotado
A por Ac
Ω Ω

8. Exemplo simples do uso dos termos
mencionados anteriormente
Fenômeno Aleatório – Jogar um dado de seis faces.
Espaço Amostral – Ω = {1, 2, 3, 4, 5, 6}.
Evento A –Sair um número par A={2, 4, 6}.
Evento B –Sair o número 2 B={2}.
1 3 5
2 4 6
Ω

9. Exemplo para clarear a
definição de espaço amostral
Fenômeno aleatório: Jogar um dado duas vezes.
Descreva o espaço amostral.
Início : 1a jogada
1 2 3 4 5 6
2a jogada
1 2 3 4 5 6 1 2 3 4 5 6 12 3 4 5 61 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
36 resultados

10. Espaço amostral e probabilidades
1,1 2,1 3,1 4,1 5,1 6,1
1,2 2,2 3,2 4,2 5,2 6,2
1,3 2,3 3,3 4,3 5,3 6,3
1,4 2,4 3,4 4,4 5,4 6,4
1,5 2,5 3,5 4,5 5,5 6,5
1,6 2,6 3,6 4,6 5,6 6,6
Evento A: A soma dos dados é igual a 4. A={(1,3);(2,2);(3,1)}
Evento B: A soma dos dados é igual a 11 B={(5,6);(6,5)}
Evento C: A soma é 4 ou 11. C={(1,3);(2,2);(3,1);(5,6);(6,5)}

11. O que é probabilidade?
• Probabilidade é uma afirmação numérica sobre
a possibilidade de que algo ocorra, quantifica o
grau de incerteza dos eventos, variando de 0 a
1 ou 0% a 100%.
• Formalmente, probabilidade é uma função P(.)
que atribui valores numéricos aos eventos de
um espaço amostral:

12. Função probabilidade
Def: Uma função P(.) é denominada probabilidade
se satisfaz as condições:
1. 0  P(A)  1,  AΩ;

2. P(Ω)=1 e P()=0;
3. Para Aj eventos disjuntos:
 n  n
P  A j    P ( A j )
  j 1
 j 1 

13. Como atribuir probabilidades aos
elementos do espaço amostral?
• Existem duas maneiras:
1. Interpretação frequentista:
Observando as diversas repetições do fenômeno em que
ocorre a variável de interesse, podemos anotar o
número de ocorrências de cada valor dessa variável,
ou seja, obtemos as probabilidades através das
frequências de ocorrências.
Para um número grande de realizações (n) a frequência
relativa pode ser usada como probabilidade.

14. Ou seja,
fri(A)= número de repetições em que ocorre A = fi
n n
2. Probabilidade teórica P(A):
Atribuir as probabilidades baseando-se em
características teóricas da realização do
fenômeno.
Quando n cresce: fr(A)  P(A)

15. Exemplo
Lançar um dado, admitindo que o dado foi construído de
forma homogênea e com medidas rigorosamente
simétricas (dado não viciado).
Da primeira maneira: podemos jogar o dado 30 vezes e
anotar as saídas, montar uma tabela de frequências e a
probabilidade de ocorrência será igual a frequência
relativa de cada observação. (exercício)
Da segunda maneira: Não temos nenhuma razão para
privilegiar uma ou outra face do dado, pois ele é não
viciado. Então podemos considerar que todas as faces
tem a mesma probabilidade de ocorrência, ou seja:
P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=1/6.

16. Exercício
• Na tabela temos dados referentes a alunos matriculados
em quatro cursos de uma universidade no ano passado:
Sexo Homens Mulheres
Curso (H) (F) Total (cursos)
Matemática Pura (M) 70 40 110
Matemática Aplicada (A) 15 15 30
Estatística (E) 10 20 30
Computação (C.) 20 10 30
Total (sexo) 115 85 200
• Considere M o evento de escolher ao acaso um aluno e
ele estar matriculado no curso de matemática pura.

17. 1. Descreva graficamente o espaço amostral.
2. Qual a probabilidade de escolher um aluno matriculado
no curso de matemática pura? (P(M)?)
3. Qual a probabilidade do aluno ser do sexo masculino?
(P(H)?)
4. Qual a probabilidade de um aluno ser homem e estar
matriculado no curso matemática aplicada? (P(AH)?)
5. Qual a probabilidade de um aluno estar matriculado em
matemática aplicada ou ser homem? (P(AH)?)

18. Resposta
1. Descrever o espaço amostral:
M A E C
H F

19. 2. P(M)?
P(M)=110/200
3. P(H)?
P(H)=115/200
4. P(AH)?
P(AH)=15/200
Sexo Homens Mulheres
Curso (H) (F) Total (cursos)
Matemática Pura (M) 70 40 110
Matemática Aplicada (A) 15 15 30
Estatística (E) 10 20 30
Computação (C.) 20 10 30
Total (sexo) 115 85 200

20. 5. P(AH)?
M A E C
F
H
P(AH)=P(A)+P(H)-P(AH)
= 30/200 + 115/200 – 15/200
= 130/200

21. • Considerando agora a união dos eventos A e C:
P(AC)=P(A)+P(C)-P(AC)
= 30/200 + 30/200 – 0
= 60/200
Os eventos A e C são disjuntos ou mutuamente
exclusivos.
M A E C

22. Regra da adição de probabilidades
• Considere os eventos U e V quaisquer, a
regra da adição de probabilidades é dada
por:
P(UV)=P(U)+P(V)-P(UV)
• Se U e V forem eventos mutuamente exclusivos
ou disjuntos, a regra é dada por:
P(UV)=P(U)+P(V)

23. Evento complementar
• Suponha agora que queremos calcular a probabilidade de
aluno NÃO estar matriculado no curso da computação:
M A E C
• P(Cc)= P(Ω) - P(C) = 1- P(C) = 1-30/200 = 170/200

24. Propriedades
1. P(A)+P(Ac)=1 9. AAc= Ω
2. (AB)c=AcBc 10. AΩ = Ω
3. (AB)c=AcBc 11. A = A
4. A= 12. A(BC)=
5. AΩ=A (AB) (AC)
6.  c= Ω
7. Ω c= 
8. AAc= 

25. Mega Sena
Dezenas Custo
• O jogo da mega sena
6 1,00
consiste em escolher 6 7 7,00
dezenas entre 60. O jogador 8 28,00
pode marcar num cartão de 6 9 84,00
a 15 dezenas. Os custos (em 10 210,00
reais) de cada jogo estão 11 462,00
12 924,00
relacionados na tabela:
13 1716,00
14 3005,00
15 5005,00

26. • Temos, ao todo  60   50.063.860 possibilidades.
 
 
6
• Qual é a probabilidade de ganhar o prêmio
máximo?
• Porque o jogo com 7 dezenas custa R$ 7,00?

27. • Resposta 1: A probabilidade de ganhar o
prêmio máximo é 1 , ou seja, uma
 60 
 
6
 
chance em 50 milhões.
• Resposta 2: Porque com 7 dezenas
podemos formar  7   7 jogos de 7
 
 6
dezenas.  
• Ou seja, fazer um jogo com 7 dezenas ou
7 jogos com 6 dezenas são ações
equiprováveis (equivalentes em termo de
probabilidade ganhar).

28. Exercício
• Considere o lançamento de dois dados.
Considere o evento A = soma dos números
obtidos igual a 9 e o evento B = número no
primeiro dado maior ou igual a 4.
• Enumere os elementos de A e B.
• Obtenha de AB, AB e Ac.
• Obtenha as probabilidades do ítem anterior.

29. Exercício
Dois dados são jogados e sua soma é anotada.
1,1 2,1 3,1 4,1 5,1 6,1
1,2 2,2 3,2 4,2 5,2 6,2
1,3 2,3 3,3 4,3 5,3 6,3
1,4 2,4 3,4 4,4 5,4 6,4
1,5 2,5 3,5 4,5 5,5 6,5
1,6 2,6 3,6 4,6 5,6 6,6
Detemine a probabilidade de que a soma seja 4. 3/36 = 1/12 = 0,083
Determine a probabilidade de que a soma seja 11. 2/36 = 1/18 = 0,056
Determine a probabilidade de que a soma seja 4 ou 11. (3+2)/36 = 0,139

30. Exercício
• De um grupo de duas mulheres(M) e três
homens (H), uma pessoa será sorteada
para presidir uma reunião. Queremos
saber qual a probabilidade de o presidente
ser do sexo masculino ou feminino?
• Defina o espaço amostral. Ω = {H,M}
• Defina o evento. E1 = {H} ou E2={M}
• Calcule as probabilidades. P(E1)=3/5
P(E2)=2/5