Este documento apresenta os principais tópicos de um curso de Bioestatística. Aborda conceitos básicos de estatística, estatística descritiva, probabilidade, amostragem, distribuições amostrais, testes de hipóteses, correlação e regressão. Inclui exemplos de tabelas, gráficos e conceitos importantes para cada tópico.







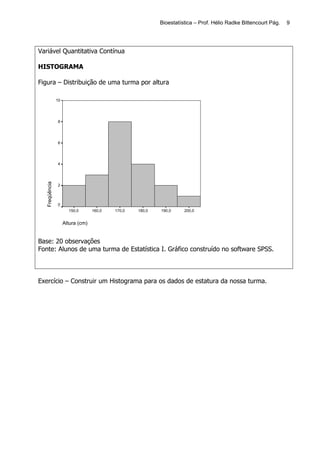

![Bioestatística – Prof. Hélio Radke Bittencourt Pág. 11
2.3.2 – Mediana (Md)
A mediana é o valor que divide o conjunto de dados ordenado em duas partes com
igual número de observações. Para calcular a mediana iremos utilizar uma nova
notação. Seja x[1] , x[ 2 ] , K, x[ n ] um conjunto de dados ordenado (ordem crescente),
onde o valor entre colchetes representa a posição no conjunto ordenado.
Deduzindo a posição mediana:
n ímpar n par
n Fila Md n Fila Md
3 4
5 6
7 8
As expressões genéricas para encontrar a média são:
n ímpar n par
Quando os dados estão organizados na forma de uma tabela de freqüências pode-se
encontrar a posição mediana na coluna acumulada Fi.
Exemplo 4 – Número de pessoas que mora em nosso domicílio
Encontrar a Md para o exemplo do número de pessoas que mora no domicílio.](https://image.slidesharecdn.com/bioestatistica-120324212145-phpapp02/85/Bioestatistica-11-320.jpg)