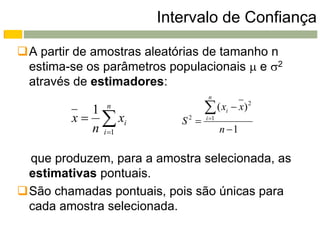
O documento discute intervalos de confiança, que fornecem um intervalo de valores plausíveis para um parâmetro populacional com base em dados amostrais. Intervalos de confiança são úteis quando se deseja estimar parâmetros com uma margem de erro conhecida.

1. Intervalo de Confiança
Profa. Dra. Juliana Garcia
Cespedes

2. Intervalo de Confiança
Quando o interesse é um determinado
parâmetro de uma população:
– Retira-se uma amostra aleatória dessa
população
– E, através desta amostra, estima-se o
parâmetro populacional.

3. Intervalo de Confiança
A partir de amostras aleatórias de tamanho n
estima-se os parâmetros populacionais  e 2
através de estimadores:
n
1 n
 ( xi  x) 2
x   xi S2  i 1
n i 1 n 1
que produzem, para a amostra selecionada, as
estimativas pontuais.
São chamadas pontuais, pois são únicas para
cada amostra selecionada.

4. Intervalo de Confiança
Um estimador T do parâmetro  é qualquer
função das observações da amostra. (É uma
estatística T, porém associada a um parâmetro
populacional)
Estimativa é o valor assumido pelo estimador em
uma particular amostra.

5. Intervalo de Confiança
Contudo, o valor estimado geralmente não será
exatamente igual ao valor verdadeiro.
Seria interessante medir o possível erro cometido
na estimação.
Uma maneira de expressar a precisão da
estimação é estabelecer limites, que com certa
probabilidade incluam o verdadeiro valor do
parâmetro.

6. Intervalo de Confiança
Esses limites são chamados de limites de
confiança e determinam um intervalo de
confiança que forneça um intervalo de valores
plausíveis para o parâmetro baseado nos dados
amostrais.
Como obter estimativas intervalares para o
parâmetro de interesse, isto é, como determinar
intervalos com limites que abranjam o valor do
parâmetro populacional, com uma margem de
segurança prefixada?

7. Intervalo de Confiança
Seja (X1,X2,...,Xn) uma amostra aleatória de
tamanho n de uma população e  o parâmetro de
^ ^
interesse. Sejam 1 e 2 estatística tais que:
=1-  é
chamado de
ˆ ˆ
P(1     2 )  1   coeficiente de
confiança
Então o intervalo (1; 2) é chamado intervalo de
^ ^
100(1-)% de confiança para o parâmetro .
Usualmente assume-se 1- = 0,95 ou 0,99

8. Interpretação - Intervalo de Confiança
Um intervalo de confiança de 95% fornece um
intervalo no qual estaríamos 95% confiantes da
cobertura do verdadeiro valor do parâmetro
Tecnicamente, 95% de todos os intervalos de
confiança que construirmos conterão o verdadeiro
valor do parâmetro (dado que todas as suposições
envolvidas estejam corretas).

9. Se obtivermos um intervalo de confiança para o
parâmetro  para cada uma dentre 100 amostras
aleatórias da população, somente 5, em média
destes intervalos de confiança não conterão .
X

1 2 3 4 ..... 100 amostras

10. Intervalo de confiança para média 
 Como encontrar os limites de confiança?
Se n > 30
Do Teorema do limite central sabe-se que:
 2  X  X 
X ~ N  ,  Z  ~ N 0,1
 n   S
  n n

11. Intervalo de confiança para média 
O intervalo de confiança para X é dado por:
 
ˆ
 

P X 1  X  X 2  P  z / 2 
X 
S

 z / 2  
 
 n 
 S S 
P X  z / 2    X  z / 2   1
 n n
 S S 
IC   X  z / 2 ; X  z / 2 
 n n

12. Intervalo de confiança para média 
Se n  30
Sabe-se que: X 
t ~ t  n 1
S
n
O IC para a média é dado por:
 S S 
P X  tn1    X  tn1   1
 n n
 S S 
IC   X  tn1 ; X  tn1 
 n n

13. Exemplo 1
Considere uma amostra de 9 elementos de uma
população:
10, 4, 8, 11, 14, 12, 9, 13, 9
Determinar:
A estimativa da média populacional
A estimativa da variância populacional
O intervalo de 95% de confiança para a média
populacional.

14. Exemplo 1
10  4  8  ...  9
X  10
9
(10  10) 2  (4  10) 2  ...  (9  10) 2
S2  9
8
  9  1  8  t  2,306
 S 
IC ,95%  X  t 
1-p
 n
p p
3
2 2  10  2,306
3
-t 0 t IC ,95%  (7,69 ; 12,31)

15. Conclusões
• Um estimador pontual para  é dado pela média
amostral.
X 1  X 2  ...  X n
X
n
• Um estimador intervalar, ou intervalo de
confiança, para  tem a forma:
X   ; X  
• Sendo  chamado de erro amostral calculado a
partir da distribuição de probabilidade de X .

16. Conclusões
 A partir do teorema do limite central, se X tem distribuição
Normal com média  e variância 2, então X tem
distribuição normal exata para todo n com média  e
variância 2/n, chamado de erro padrão da média.
 Conhecendo-se o coeficiente de confiança  = 1- obtém-
se o valor de z.
 Então, da equação do intervalo de confiança para a média
 tem-se a equação do erro amostral:

z
n

17. Exercício 1
Uma amostra de 9 elementos de uma população
forneceu os seguintes valores:
1, 2, 4, 4, 5, 5, 7, 8, 9
Determinar:
A estimativa da média populacional
A estimativa da variância populacional
Os intervalos de 90%, 95% e 99% de confiança para
a média populacional e interprete o resultado.

18. Exercício 2
 Seja X uma v.a. com distribuição normal de média e
variância desconhecidas, considere que a variância
amostral é igual a 36.
a) Para uma amostra de tamanho 50, obtivemos média
amostral 18,5. Construa um intervalo de confiança com
coeficientes de confiança 91%, 94% e 99% para a
média populacional.
b) Para uma confiança de 96%, construa intervalos de
confiança supondo três tamanhos de amostra 25, 50 e
100 (admita que todos forneceram média amostral igual
a 18,5).
c) Comente sobre a precisão dos intervalos construídos
em (a) e (b).

19. Exercício 3
 O intervalo [34,81 ; 36,38], com confiança 95%
foi construído a partir de uma amostra de
tamanho 25, para a média de uma população.
O desvio padrão amostral foi igual a 2.
a. Qual o valor encontrado para a média dessa
amostra?
b. Se utilizássemos essa mesma amostra, mas
com uma confiança de 90%, qual seria o novo
intervalo de confiança?

20. Exercício 4
 O tempo de permanência de contadores recém
formados no primeiro emprego, em anos, foi estudado
considerando um modelo normal com média e variância
desconhecidas.
 Deseja-se estimar a média populacional. Para uma
amostra de 15 profissionais, a média obtida foi de 2,7
anos e o desvio padrão foi de 1,4 anos.
a. Encontre um intervalo para o tempo médio populacional
de permanência com uma confiança de 90%.
b. Refaça o item a. considerando que a amostra era
formada por 150 profissionais.