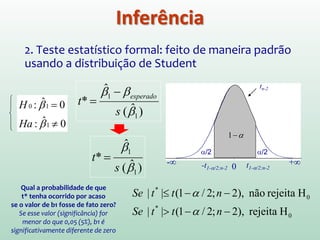
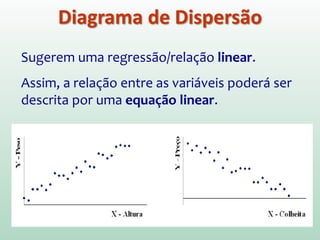
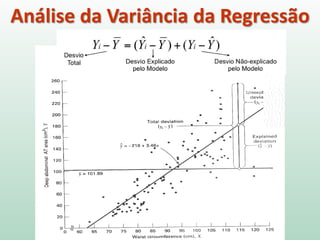
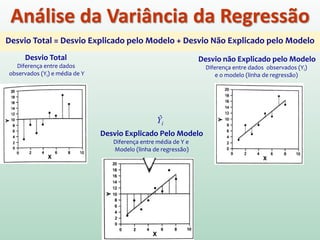
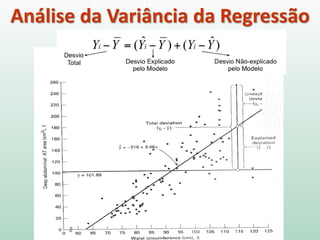
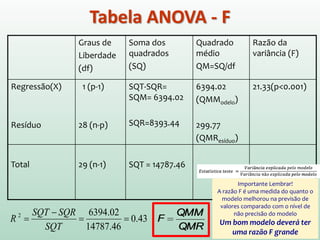
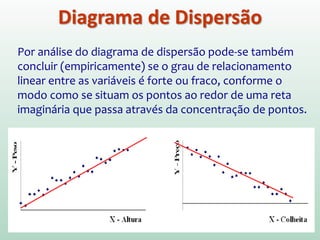
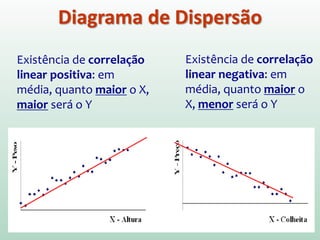
1) O documento apresenta os conceitos e métodos de regressão linear, incluindo estimação de parâmetros, avaliação do ajuste do modelo e interpretação dos resultados. 2) A regressão linear é usada para modelar a relação entre uma variável dependente e uma ou mais variáveis independentes através de uma equação linear. 3) A qualidade de ajuste do modelo é avaliada por meio da análise da variância, que parte a soma dos quadrados total em parte explicada pelo modelo e parte residual.

1. REGRESSÃO LINEAR
Parte I
Vitor Vieira Vasconcelos
Flávia da Fonseca Feitosa
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Julho de 2017

2. Conteúdo
• Revisão
 Modelos
 Correlação
 Teste de Significância
• Regressão Linear
 Estimação dos parâmetros
 Avaliação do ajuste do modelo
 Interpretação dos resultados

3. Leitura de Referência
Capítulo 5
Regressão
(p. 156-168)

4. Inferência Estatística se
resumindo a uma equação…
Saídai = (Modeloi) + erroi
Ou seja, os dados que observamos podem ser
previstos pelo modelo que escolhemos para
ajustar os dados mais um erro

5. Média como um modelo estatístico
Uma maneira útil de descrever um grupo como
um todo:
• Qual é a renda média das famílias residentes na
Mooca?
• Qual é a altura média dos edifícios em São
Caetano?
• Qual é o PIB médio dos municípios localizados
no arco do desmatamento?

6. Para além de médias… Modelos Lineares
 São modelos baseados sobre uma linha reta,
utilizados para representar a relação entre variáveis
 Ou seja, geralmente estamos tentando resumir as
RELAÇÕES observadas a partir de nossos dados
observados em termos de uma linha reta.
ConsumodeÁguaper
Capita(m3/dia/ano)
Renda per Capita (R$)
RELAÇÃO ENTRE
CONSUMO DE ÁGUA E
RENDA

7. CORRELAÇÃO
É uma medida do relacionamento linear
entre duas variáveis
Duas variáveis podem estar:
(a)Positivamente relacionadas 
quando maior a renda, maior o consumo de água
(b)Negativamente relacionadas 
quanto maior a renda, menor o consumo de água
(c)Não há relação entre as variáveis

8. Correlação de Pearson
Medida padronizada da correlação entre variáveis
Valor de r situa-se entre -1 e +1
r = +1  duas variáveis estão perfeitamente correlacionadas de forma positiva
(se uma aumenta, a outra aumenta proporcionalmente)
r = -1  relacionamento negativo perfeito (se uma aumenta, a outra diminui
em valor proporcional
r = 0  indica ausência de relacionamento linear
COEFICIENTE DE CORRELAÇÃO DE PEARSON

9. Teste de Significância do r de Pearson
Para testar a significância do r, calculamos uma estatística
teste conhecida como “razão t”, com graus de liberdade
igual a N-2.
Olhar na tabela o valor crítico de t, com graus de liberdade
“N-2” e α=0,05
Se tcalculado > tcrítico, podemos rejeitar a hipótese nula de que
ρ=0.
Neste caso, os graus de
liberdade indicam o quão
próxima a distribuição t está da
distribuição normal. Qto maior,
mais póximo da dist. normal.

10. ANÁLISE DE REGRESSÃO
CORRELAÇÃO: Indica a força e a direção do
relacionamento linear entre duas variáveis
aleatórias
Vamos avançar um passo:
Obter uma equação matemática que
descreva a relação entre duas ou mais
variáveis.
Esta é a essência da
(Lembrando que não estamos lidando com relações de causa-efeito)

11. Análise de regressão é uma ferramenta estatística
que permite explorar e inferir a relação de uma
variável dependente (Y  variável resposta/
dependente/ saída) com variáveis independentes
específicas (X  variáveis indicadoras/ previsoras/
explicativas/ independentes).
Y = aX + b
NETER J. et al. Applied Linear Statistical Models. Boston, MA: McGraw-Hill, 1996.
ANÁLISE DE REGRESSÃO

12.  Criminalidade (+) X Renda (-), Investimentos (-)
 Longevidade (+) X Escolaridade (+), Renda (+)
 Consumo de Água (+) X Renda per Capita (+)
 Outros exemplos? ...
Exemplo

13. 1. Determinar como duas ou mais variáveis se
relacionam.
2. Estimar a função que determina a relação entre
duas variáveis.
3. Usar a equação para projetar/estimar valores da
variável dependente.
Lembrete importante: A existência de uma relação
estatística entre a variável resposta Y e a variável
explicativa X não implica na existência de uma relação
causal entre elas.
Objetivos da Análise de Regressão

14. Os dados para a análise de regressão são da forma:
(x1, y1), (x2, y2), ..., (xi, yi), ... (xn, yn)
Com os dados constrói-se o diagrama de dispersão.
Este deve exibir uma tendência linear para que se
possa usar a regressão linear.
Ou seja, o diagrama permite decidir empiricamente
se um relacionamento linear entre X e Y deve ser
assumido.
Diagrama de Dispersão

15. Sugerem uma regressão/relação linear.
Assim, a relação entre as variáveis poderá ser
descrita por uma equação linear.
Diagrama de Dispersão

16. Sugerem uma regressão/relação não linear.
Assim, a relação entre as variáveis poderá ser
descrita por uma equação não linear.
(ou podemos verificar a possibilidade de “linearizar” a relação
através de transformações nas variáveis)
Diagrama de Dispersão

17. Por análise do diagrama de dispersão pode-se também
concluir (empiricamente) se o grau de relacionamento
linear entre as variáveis é forte ou fraco, conforme o
modo como se situam os pontos ao redor de uma reta
imaginária que passa através da concentração de pontos.
Diagrama de Dispersão

18. Diagrama de Dispersão
Existência de correlação
linear positiva: em
média, quanto maior o X,
maior será o Y
Existência de correlação
linear negativa: em
média, quanto maior o
X, menor será o Y

19. Um modelo de regressão contendo somente
uma variável preditora (X) é denominado
modelo de regressão simples.
Um modelo com mais de uma variável
preditora (X) é denominado
modelo de regressão múltiplo.
Modelos de Regressão

20. onde:
Yi é o valor da variável resposta na i-ésima observação;
β0 e β1 são parâmetros;
Xi é uma constante conhecida; é o valor da variável
preditora na i-ésima observação;
ξi é um termo de erro aleatório com média zero e variância
constante σ2 (E(ξi)=0 e σ2 (ξi)= σ2 )
ξi e ξj são não correlacionados (independentes) para i j
(σ2 (ξi,ξj)= 0 )
Regressão Linear Simples
Saídai = (Modeloi) + erroi
Lembrando:

21. Yi
ξi
X
Y
β0
β1
Coeficiente
angular
µY = E(Y) = β0 + β1 X
Inclinação
Populacional
Intercepto
Populacional
Erro
Aleatório
Variável Preditora
Variável
Resposta Yi=β0+β1Xi +εi
Ŷi=b0+b1Xi
εi =Yi-Ŷi
Modelo estimado
Resíduo
Regressão Linear Simples

22. Os parâmetros β0 e β1 são denominados coeficientes de
regressão:
1. β1 é a inclinação da reta de regressão. Ela indica a mudança
na média de Y quando X é acrescido de uma unidade.
2. β0 é o intercepto em Y da equação de regressão (é o valor de
Y quando X = 0.)
β0 só tem significado se o modelo incluir X = 0.
Significado de β0 e β1
0β
1β
Y
X
0

23. β0
θ
x x+1
∆x=1
∆y
yi = β0 + β1xi
x
y
∆
∆
=1β
β0 (intercepto): quando a região experimental inclui X=0, β0 é o valor da
média da distribuição de Y em X=0, cc, não tem significado prático como um
termo separado (isolado) no modelo;
β1 (inclinação): expressa a taxa de mudança em Y, isto é, é a mudança em Y
quando ocorre a mudança de uma unidade em X. Ele indica a mudança na
média da distribuição de probabilidade de Y por unidade de acréscimo em X.
Fonte: Slide de Paulo José Ogliari, Informática, UFSC. Em http://www.inf.ufsc.br/~ogliari/cursoderegressao.html

24. Como encontrar a “linha” que
melhor se ajusta aos nossos dados?
Ou seja:
Como estimar os valores de β0 e β1?
Yi
ξi
X
Y
β0
β1
Coeficiente
angular
Y = β0 + β1 X

25. Em geral não se conhece os valores de β0 e β1 .
Eles podem ser estimados através de dados obtidos por
amostras.
O método utilizado na estimação dos parâmetros é o
método dos mínimos quadrados, o qual considera os
desvios dos Yi de seu valor esperado (E(Yi )):
ξi = Yi – (β0 + β1 Xi)
Estimação dos Parâmetros
Ŷi
Ŷi=b0+b1Xi
εi =Yi-Ŷi

26. Em particular, o método dos mínimos
quadrados requer que a soma dos n desvios
quadrados, denotado por Q, seja mínima:
2
10
1
][ ii
n
i
XYQ ββ −−= ∑=
Estimação dos Parâmetros

27. Procedimento matemático para minimizar Q (soma dos desvios
quadrados):
(1) Q deve ser derivado em relação a β0 e β1:
(1) Com derivadas parciais igualadas à zero, obtêm-se os valores
estimados de β0 e β1:
∑
∑
=
=
−
−−
= n
i
i
n
i
ii
XX
YYXX
1
2
1
1
)(
))((
ˆβ
XY 10 ˆˆ ββ −=
∑
∑
=
∂
∂
=
∂
∂
−−−=
−−−=
n
i
iii
Q
n
i
ii
Q
XYX
XY
1
10
1
10
)(2
)(2
1
0
ββ
ββ
β
β
Estimação dos Parâmetros
Os estimadores β0 e β1 possuem distribuição
normal e intervalos de confiança com uma
distribuição t, com n-2 graus de liberdade
Derivação
1ˆβ
Q

28. Correlação linear
 Não determina causalidade,
mas pode dar pistas.
 Pode ser testada
estatisticamente.
 Identifica se duas variáveis se
relacionam de forma linear.
 Determina o quão mais
próximo de uma reta é a
relação entre as variáveis.
 0: não há relação linear
 1: relação linear perfeita
 Não indica o quanto uma
variável pode estar
influenciando a outra.
Regressão linear
 Não determina causalidade,
mas pode dar pistas.
 Pode ser testada
estatisticamente
 Determina uma relação
linear entre duas variáveis.
 Traz elementos que
permitem fazer predições.
 Identifica o quanto uma
variável afeta a outra.
 Necessita de uma análise dos
resíduos para decidir sobre
sua adequação.
Slides: Marcos Pó
Correlação vs. Regressão

29. Como avaliar o quão bem nossa
“linha” adere aos dados?
Ou seja:
Como avaliar a qualidade de ajuste
do modelo?

30. Análise da Variância da Regressão

31. Análise da Variância da Regressão
Desvio Total
Diferença entre dados
observados (Yi) e média de Y
Desvio não Explicado pelo Modelo
Diferença entre dados observados (Yi)
e o modelo (linha de regressão)
Desvio Explicado Pelo Modelo
Diferença entre média de Y e
Modelo (linha de regressão)
Desvio Total = Desvio Explicado pelo Modelo + Desvio Não Explicado pelo Modelo
Ŷi

32. Análise da Variância da Regressão

33. )ˆ()ˆ( YYYYYY iii −+−=−
Elevando-se ao quadrado os dois lados da igualdade e fazendo-se
a soma para todas as observações de uma determinada amostra
tem-se que:
Soma dos quadrados
total (SQT)
Soma dos quadrados
do modelo (SQM)
Soma dos quadrados
residual (SQR)
Desvio
Total Desvio Explicado
pelo Modelo
Desvio Não-explicado
pelo Modelo
Inferência: Análise da Variância

34. Se SQT=0, então todas as
observações Y são iguais.
Quanto maior for SQT,
maior será a variação entre
os Y’s.
SQT é uma medida da
variação dos Y’s quando
não se leva em
consideração a variável
independente X.
Se SQR = 0, então as
observações caem na
linha de regressão.
Quanto maior SQR,
maior será a variação
das observações Y
ao redor da linha de
regressão.
Se a linha de regressão
for horizontal, de modo
que então
SQM = 0.
0
^
=−
−
YYi
Particionando a Soma dos Quadrados
SQT SQM SQR

35. SQTotal = SQModelo + SQResíduos.
Um modo de se saber quão útil será a linha de
regressão para a predição é verificar quanto da SQT
está na SQM e quanto está na SQR.
Idealmente, gostaríamos que SQM fosse muito maior
que SQR.
Gostaríamos, portanto, que fosse próximo de 1.
SQT
SQM
Particionando a Soma dos Quadrados

36. Uma medida do efeito de X em reduzir a
variabilidade do Y é:
Note que: 0 ≤ R2 ≤ 1
R2 é denominado coeficiente de determinação. Em
um modelo de regressão simples, o coeficiente de
determinação é o quadrado do coeficiente de
correlação de Pearson (r) entre Y e X. Note que em
um modelo de regressão simples
SQT
SQR
1
SQT
SQR-SQT
SQT
SQM2
−===R
112
≤≤−⇒±= rRr
Coeficiente de Determinação
SQTotal = SQModelo + SQResíduos

37. Temos dois casos extremos:
R2 = 1 todas as observações caem na linha de
regressão ajustada. A variável preditora X explica
toda a variação nas observações.
R2 = 0 isto ocorre quando b1 = 0. Não existe
relação linear em Y e X. A variável X não ajuda a
explicar a variação dos Yi .
Coeficiente de Determinação

38. Outra maneira de avaliar o modelo
utilizando a soma dos quadrados é por
meio do Teste F
O Teste F tem por base a razão F, que é a razão
de melhoria devida ao modelo e a diferença
entre o modelo e os dados observados
A razão F é uma medida do quanto o modelo
melhorou na previsão de valores comparado
com o nível de não precisão do modelo

39. Graus de
Liberdade
(df)
Soma dos
quadrados
(SQ)
Quadrado
médio
QM=SQ/df
Razão da
variância (F)
Regressão(X)
Resíduo
1 (p-1)
28 (n-p)
SQT-SQR=
SQM= 6394.02
SQR=8393.44
6394.02
(QMModelo)
299.77
(QMResíduo)
21.33 (p<0.001)
Total 29 (n-1) SQT = 14787.46
43.0
46.14787
02.63942
==
−
=
SQT
SQRSQT
R
Tabela ANOVA - F

40. Graus de
Liberdade
(df)
Soma dos
quadrados
(SQ)
Quadrado
médio
QM=SQ/df
Razão da
variância (F)
Regressão(X)
Resíduo
1 (p-1)
28 (n-p)
SQT-SQR=
SQM= 6394.02
SQR=8393.44
6394.02
(QMModelo)
299.77
(QMResíduo)
21.33(p<0.001)
Total 29 (n-1) SQT = 14787.46
43.0
46.14787
02.63942
==
−
=
SQT
SQRSQT
R
Tabela ANOVA - F
Importante Lembrar!
A razão F é uma medida do quanto o
modelo melhorou na previsão de
valores comparado com o nível de
não precisão do modelo
Um bom modelo deverá ter
uma razão F grande

41. 0:
0ˆ...ˆˆ: 210
≠
===
jdosummenospeloexisteH
H
a
k
β
βββ
onde Fc ~ F p-1, n-p
Se F*> F (α; p-1,n-p), rejeitamos a hipótese nula, caso contrário,
aceitamos a hipótese.
Inferência: Teste F
(Adequação Global)

42. -∞ +∞0 t1-a/2;n-2
tn-2
-t1-a/2;n-2
1 α−
a/2a/2
1. Construir intervalos de confiança para :
2. Teste de hipótese para :
0ˆ:
0ˆ:
1
10
≠
=
β
β
aH
H
Se = 0 , significa que não há correlação entre X e Y.
Rejeitar , significa que o modelo que inclui X é melhor do que o
modelo que não inclui X, mesmo que a linha reta não seja a relação mais
apropriada.
1ˆβTestando se a inclinação é zero.
0H
Inferência: Significância de b

43. 1. Construir intervalos de confiança para:1ˆβ
∑
∑
=
=
−
−−
= n
i
i
n
i
ii
XX
YYXX
1
2
1
1
)(
))((
ˆβ
Média:
Variância
estimada: ( )∑
= −
2)ˆ( 1
2
XX
QMR
i
s β
).2(~
)ˆ(
ˆ
1
11
−
−
nt
s β
ββ
Distribuição da estatística studentizada (σ é desconhecido)
Intervalo de confiança
)ˆ()2;2/1(ˆ
11 βαβ snt −−±
Inferência

44. 2. Teste estatístico formal: feito de maneira padrão
usando a distribuição de Student
-∞ +∞0 t1-α/2;n-2
tn-2
-t1-α/2;n-2
1 α−
α/2α/2
)ˆ(
ˆ
*
1
1
β
ββ
s
t
esperado−
=
0
*
0
*
Hrejeita),2;2/1(||
Hrejeitanão),2;2/1(||
−−>
−−≤
nttSe
nttSe
α
α
Inferência
)ˆ(
ˆ
*
1
1
β
β
s
t =
Qual a probabilidade de que
t* tenha ocorrido por acaso
se o valor de b1 fosse de fato zero?
Se esse valor (significância) for
menor do que 0,05 (5%), b1 é
significativamente diferente de zero
0ˆ:
0ˆ:
1
10
≠
=
β
β
aH
H

45. 0:H
0:H
01
00
≠
=
β
β
Se a hipótese nula H0= 0 não for rejeitada, pode-se
excluir a constante do modelo, já que a reta inclui a
origem.
0
ˆβDe forma semelhante testamos se é zero
Inferência

46. Executando uma Regressão
Simples no SPSS

47. Regressão Simples no SPSS
1. No SPSS, abra o arquivo
“Agua2010_SNIS.sav”
1. Vá em Analisar >
Regressão > Linear
(Analyze > Regression > Linear )
Selecione a variável “dependente” e
“independente”
Existe uma variedade de opções disponíveis, mas
serão exploradas no contexto da regressão múltipla.

48. Ajuste Global do Modelo
Resumo do Modelo
R = 0,601  Como temos apenas um previsor, este valor representa a
correlação simples entre Y (renda) e X (consumo).
R2 = 0,362  Coeficiente de Determinação. Nos informa que nosso modelo
consegue explicar 36,2% da variação do consumo de água. Devem existir
muitos fatores que podem explicar esta variação, mas nosso modelo, que
inclui somente a renda per capita, pode explicar 36,2% dela. No entanto, 63,8%
da variação do consumo de água não pode ser explicada pela variação da
renda per capita.

49. Ajuste Global do Modelo
Análise de Variância
Soma dos Quadrados do Modelo (SQM), Soma dos Quadrados dos Resíduos
(SQR) e Soma dos Quadrados Total (SQT)
Lembrando: SQT = SQM + SQR
Razão F = Quadrado Médio do Modelo / Quadrado Médio do Resíduo
Razão F = 2499,709 (É um número bem grande!!! O que isso significa?)

50. Ajuste Global do Modelo
Análise de Variância
Para estes dados, F é 2499.709, que é significativo ao nível de p<0,001 (pois o
valor na coluna Sig. é menor do que 0,001)
Esse resultado nos informa que existe uma probabilidade menor do que 0,1%
de que um valor F tão alto tenha ocorrido apenas por acaso. Ou seja, pode-se
concluir que nosso modelo de regressão representa melhor o consumo de
água do que se tivéssemos usado apenas o valor médio do consumo.

51. Parâmetros do Modelo
A análise de variância apresentada na tabela ANOVA nos informa se o
modelo, em geral, resulta em um grau de previsão significativamente bom
dos valores da variável de saída (no caso, consumo de água). No entanto, a
ANOVA não nos informa sobre a contribuição individual das variáveis no
modelo (embora neste caso simples exista uma única variável X no modelo
e, assim, podemos inferir que esta variável é um bom previsor.)
A tabela dos coeficientes fornece detalhes dos parâmetros do modelo (os
valores beta) e da significância desses valores.

52. Parâmetros do Modelo
b0= intercepto y (ponto onde a linha corta o eixo y)  b0= 4,252 (Valor que Y
assume quando X=0)
b1= inclinação reta de regressão  Mudança da variável de saída (Y) para cada
alteração de uma unidade no previsor (X)
b1= 0,041  Em média, um aumento de R$ 1 na renda per capita, está
relacionado a um aumento de 0,041 m3/ano de consumo de água (41 litros/ano)
Esta variável preditora (renda) está tendo impacto?

53. Parâmetros do Modelo
Esta variável preditora (renda) está tendo impacto?
Para isso, b1 deve ser diferente de zero!!! O teste t nos informa se b1 difere de
zero.
Em “Sig.” temos a probabilidade de que o valor de t ocorra se o valor de b é zero.
Se esta probabilidade é menor do 0,05 (5%) aceita-se que o resultado reflete um
efeito genuíno, não é fruto do acaso.
Como as probabilidades são próximas de 0,000 (zero até a terceira casa),
podemos dizer que a esta probabilidade é menor do que 0,001 (p<0,001).
Concluímos que a renda tem uma contribuição significativa (p<0,001) na
explicação da variação do consumo de água.