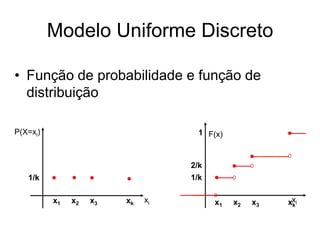
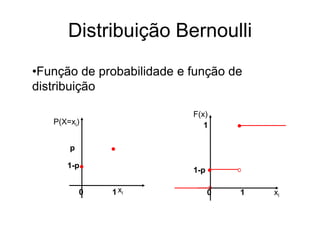
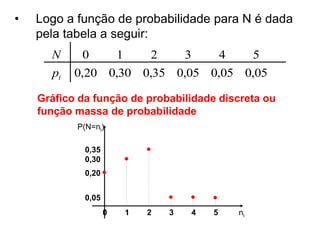
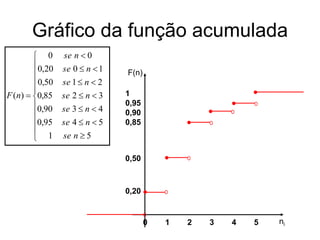
O documento apresenta os conceitos fundamentais de variável aleatória discreta, incluindo: 1) Definição de variável aleatória e exemplos de variáveis aleatórias discretas e contínuas; 2) Função de probabilidade discreta e função de distribuição de probabilidade; 3) Cálculo de média, mediana, moda e variância para variáveis aleatórias discretas.

1. Aula 7
Variáveis aleatórias
Profa. Dra. Juliana Garcia Cespedes

2. Variável aleatória
• Agora vamos formalizar, com a ajuda da Teoria das
probabilidades, o comportamento de variáveis na
população.
• Uma variável aleatória é uma quantidade X, associada a
cada possível resultado do espaço amostral.
a b c d e f Ω
X
x1 x2 x3 x4

3. Variável aleatória
• Variável aleatória discreta se assume valores
num conjunto enumerável, com certa
probabilidade.
Ex: Número de filhos em famílias.
• Variável aleatória contínua se seu conjunto de
valores é qualquer intervalo dos números reais,
o que seria um conjunto não enumerável.
Ex: Peso e altura dos filhos.

4. Variável aleatória discreta

5. Função de probabilidade discreta
• Chama-se função de probabilidade da variável
aleatória discreta X, que assume os valores x1, x2, ..., xx,
..., a função p(xi) que a cada valor de xi associa a sua
probabilidade de ocorrência, isto é,
p( xi )  P( X  xi )  pi , i  1, 2,...
• Ou ainda, Satisfaz as
propriedades:
X x1 x2 x3 ... 0  pi  1
pi p1 p2 p3 ... p
i
i 1

6. Exemplo
• Para as famílias de uma região, 20% não tem
filhos, 30% tem um filho, 35% tem dois e as
restantes se dividem igualmente entre três,
quatro ou cinco filhos. (Informações retiradas do
último censo).
• Definimos por N a variável aleatória número de
filhos.
• Os valores que a variável N pode assumir são:
0,1,2,3,4 e 5 filhos

7. • Qual é a função de probabilidade dessa
variável?
• Segue das informações disponíveis:
20% das famílias não tem filhos, então a
probabilidade de uma família sorteada ao
acaso não ter filhos é P(N=0) = 0,20.
• De forma semelhante, temos que:
P(N=1) = 0,30
P(N=2) = 0,35

8. • Falta descrever as probabilidades P(N=3),
P(N=4) e P(N=5).
• Sabemos que são iguais e digamos que tenham
valor p. Utilizando a definição de função de
probabilidade discreta, temos:
P( N  0)  P( N  1)  P( N  2)  ...  P( N  5)  1
0,20  0,30  0,35  p  p  p  1
0,85  3 p  1
0,15
p  0,05
3

9. • Logo a função de probabilidade para N é dada
pela tabela a seguir:
N 0 1 2 3 4 5
pi 0,20 0,30 0,35 0,05 0,05 0,05
Gráfico da função de probabilidade discreta ou
função massa de probabilidade
P(N=ni)
0,35
0,30
0,20
0,05
0 1 2 3 4 5 ni

10. Função de distribuição de
probabilidade
• A função de distribuição ou função
acumulada de probabilidade de uma variável
aleatória discreta X é definida, para qualquer
número real x, por:
F ( x)  P( X  x)

11. • Considere o exemplo anterior, cuja função massa de
probabilidade é dada por:
N 0 1 2 3 4 5
pi 0,20 0,30 0,35 0,05 0,05 0,05
• A função de distribuição ou função acumulada é dada
por:
 0 se n  0
F (n)  P( N  n)  0,20 se 0  n  1

 0,50 se 1  n  2

F (n)  0,85 se 2  n  3
0,90 se 3  n  4

0,95 se 4  n  5

 1 se n  5

12. Gráfico da função acumulada
 0 se n  0
 0,20 se 0  n  1
 F(n)
 0,50 se 1  n  2

F (n)  0,85 se 2  n  3 1
0,90 se 3  n  4 0,95
 0,90
0,95 se 4  n  5 0,85

 1 se n  5
0,50
0,20
0 1 2 3 4 5 ni

13. Exercício
• Um jogador paga 5 fichas para participar de um jogo de
dados, disputando com a banca quem tem o ponto maior.
O jogador e a banca lançam cada um o seu dado e a
seguinte regra de premiação é estabelecida:
• Se o ponto do jogador é maior, ele ganha 2 vezes a
diferença entre o seu ponto (j) e o obtido pela banca (b);
• Se o ponto do jogador é menor ou igual ao da banca, ele
não ganha nada.
Variável aleatória G: ganho
2( j  b), se j  b bruto do jogador em uma
G
jogada, isto é, valor
arrecadado sem descontar
0 , se j  b as fichas inicias pagas para
participar do jogo.
• O jogo é mais favorável para quem?

14. Resposta
• Para cada par sorteado (b,j), a premiação é baseada
nos seus valores. Dessa forma, se o jogador tira 3 e a
banca 1, o valor do ganho bruto do jogador será
G=2*(1-3)=4.
• Se o jogador tira 5 e a banca 6, temos G=0 pois j<b.
• O espaço amostral, correspondente a uma jogada, é
apresentado a seguir:
1,1 2,1 3,1 4,1 5,1 6,1
1,2 2,2 3,2 4,2 5,2 6,2
1,3 2,3 3,3 4,3 5,3 6,3
1,4 2,4 3,4 4,4 5,4 6,4
1,5 2,5 3,5 4,5 5,5 6,5
1,6 2,6 3,6 4,6 5,6 6,6

15. Resposta
• O valor G=0 acontecerá quando o ponto do jogador for
menor ou igual ao da banca. Isso corresponde ao
subconjunto do espaço amostral:
1,1
1,2 2,2
1,3 2,3 3,3
1,4 2,4 3,4 4,4
1,5 2,5 3,5 4,5 5,5
1,6 2,6 3,6 4,6 5,6 6,6
• Esses 21 pares tem todos a mesma probabilidade de
ocorrência e, portanto, teremos P(G=0) = 21/36

16. Resposta
• De modo análogo, calculamos os demais valores e
obtemos a função de probabilidade:
G 0 2 4 6 8 10
pi 21 / 36 5 / 36 4 / 36 3 / 36 2 / 36 1 / 36
Conclusão:
Tendo em vista as 5 fichas pagas no início, o jogador só
não terá prejuízo nos casos em que obtiver 6, 8 ou 10
fichas de retorno, o que acontece com probabilidade
3/36+2/36+1/36 = 6/36. Portanto, o jogo é altamente
favorável à banca e, somente com muita sorte (1/36), o
jogador ganhará o dobro do que apostou.

17. Valor esperado
• Dada a variável aleatória X discreta, assumindo
os valores x1, x2, ..., xn, chamamos de valor
médio ou esperança matemática de X ao valor:
n n
E ( X )     xi P( X  xi )  xi pi
i 1 i 1
Medida para a população Valor teórico de probabilidade
Valor frequentista de probabilidade
n
Medida para a amostra x   xi fri
i 1

18. Variância
• A variância da variável aleatória discreta X
é definida por:
n
var( X )   2   [ xi  E ( X )]2 pi
i 1
• O desvio padrão ( ) de X é definido como
a raiz quadrada da variância.

19. Mediana e Moda
• A mediana de uma variável aleatória discreta X
é o valor que satisfaz às seguintes condições:
1 1
P( X  Md )  e P( X  Md ) 
2 2
• A moda é o valor da variável que tem maior
probabilidade de ocorrência
P( X  Mo)  max( p1 , p2 ,..., pn )

20. Conjunto de dados Variável aleatória discreta
Valores X x1 x2 ... xn X x1 x2 ... xn
freq. fr1 fr2 ... frn pi p1 p2 ... pn
n n
x   xi fri   E ( X )   xi pi
Média
i 1 i 1
Mediana md=valor central 1 1
Md : P( X  Md )  e P( X  Md ) 
2 2
Moda mo= valor com maior Mo= valor com maior
frequência probabilidade
n
 2   ( xi   ) 2 pi
n
Variância
var( x)   ( xi  x) 2 fri
i 1
i 1
Desvio padrão dp( x)  var( x)   2

21. Principais modelos discretos
• Algumas variáveis aleatórias aparecem com
frequência em situações práticas. Em geral
nesses casos, a distribuição de probabilidade
pode ser escrita de uma maneira mais
compacta, isto é, existe uma lei para atribuir as
probabilidades.
• Ex: Uma rifa de 100 números, qual a
probabilidade de sair um número ao acaso?
Como escrever a função de probabilidade
discreta?

22. • A probabilidade de sair um número
qualquer ao acaso é 1/100.
• A função de probabilidade é dada por:
X 1 2 ... 100
pi 1 1 ... 1
100 100 100
1
P( X  xi )  ,  i  1,...,100
100

23. Modelo uniforme discreto
• Seja X uma v. a. cujos possíveis valores são
representados por x1, x2, ...,xk. Dizemos que X segue o
modelo Uniforme Discreto se atribui a mesma
probabilidade 1/k a cada um desses k valores, isto é,
sua função de probabilidade é dada por:
1
P( X  xi )  p( xi )  ,  i  1,2,..., k.
k
1 k 
1
  E ( X )   xi ,   var( X )   xi 
2 2
 xi  
2


k i 1 k k 
 

24. Modelo Uniforme Discreto
• Função de probabilidade e função de
distribuição
P(X=xi) 1 F(x)
2/k
1/k 1/k
x1 x2 x3 xk xi x1 x2 x3 xxi
k

25. Bernoulli
• Experimentos que apresentam ou não uma
determinada característica. Situações que podem
ser representadas por respostas do tipo sucesso-
fracasso.
• Exemplos
• Uma moeda é lançada: o resultado ou é cara, ou não
(ocorrendo, coroa).
• Uma peça é escolhida ao acaso de um lote de 500 peças:
essa peça é defeituosa ou não.
• Uma pessoa é escolhida ao acaso entre os moradores de
uma cidade e verifica-se se ela é favorável ou não a um
projeto municipal.

26. • Dizemos que uma v.a. X segue o modelo
Bernoulli se atribui 0 ou 1 a ocorrência de
fracasso ou sucesso, respectivamente. Com p
representando a probabilidade de sucesso, sua
função de probabilidade é dada por:
P( X  x)  p x (1  p)1 x , x  0, 1
ou seja ,
P( X  0)  1  p
P( X  1)  p
E( X )  p; Var ( X )  p(1  p)

27. Distribuição Bernoulli
•Função de probabilidade e função de
distribuição
F(x)
P(X=xi) 1
p
1-p
1-p
0 1 xi 0 1 xi

28. Binomial
• Considere a repetição de n ensaios de Bernoulli
independentes e todos com a mesma
probabilidade de sucesso p.
• Exemplos:
• Uma moeda é lançada é três vezes, qual é a probabilidade
de se obter duas caras?
• Dez peças são extraídas, ao acaso, com reposição, de um
lote contendo 500 peças, qual é a probabilidade de que
todas sejam defeituosas, sabendo-se que 10% das peças
do lote são defeituosas?
• Sabe-se que 90% das pessoas de uma cidade são
favoráveis a um projeto municipal. Escolhendo-se 100
pessoas ao acaso entre os moradores, qual é a
probabilidade de que pelo menos 80 sejam favoráveis ao
projeto?

29. • A v.a. que conta o número total de sucessos é
denominada Binomial com parâmetros n e p e
sua função de probabilidade é dada por:
n x
P( X  x)    p (1  p) n x , x  0,1, 2, ..., n
 x
 
n
 
• Com  x
 representando o coeficiente binomial
calculado por:
n n!
 
 x  x!(n  x)!
 
E( x)  np Var ( X )  np(1  p)

30. Exemplo
• Dez peças são extraídas, ao acaso, com reposição, de
um lote contendo 500 peças, qual é a probabilidade de
que todas sejam defeituosas, sabendo-se que 10% das
peças do lote são defeituosas?
• Temos n=10 ensaios de Bernoulli, cada um com
P(S)=P(peça defeituosa)=p=0,1.
• Se X indicar o número de peças defeituosas na amostra,
queremos calcular P(X=10). X ~ Bin(10; 0,1)
10  10
P( X  10)   0,1 (1  0,1)1010  0,110
10 
 

31. • Qual o valor esperado e a variância?
E ( X )  10 * 0,1  1
Var ( X )  10 * 0,1* (1  0,1)  0,9
dp( X )  0,9  0,95
• Qual é a interpretação deste resultado?

32. Poisson
• O modelo Poisson é bastante utilizado quando
se deseja contar o número de eventos de certo
tipo que ocorrem num intervalo de tempo.
Exemplos:
• Número de chamadas telefônicas recebidas por
um Call Center em 5 min;
• Número de falhas de um computador em um dia
de operação;
• Número de vendas diárias de um funcionário de
uma loja de automóveis.

33. • Uma v.a. X tem distribuição de Poisson com
parâmetro >0 se sua função de probabilidade é
dada por:

e  x
P( X  x)  , x  0,1,2,....
x!
E( X )   Var ( X )  

34. Exemplo
• Sabe-se que um Call center recebe, em média, 5
chamadas por minuto. Supondo que a distribuição de
Poisson seja adequada nessa situação, obter a
probabilidade de que o Call center não receba
chamadas durante um intervalo de 1 minuto.
5 0
e 5 5
P( X  0)   e  0,0067
0!
E( X )  5 Var ( X )  5

35. Geométrica
• Número de ensaios de Bernoulli que
precedem o primeiro sucesso.
• Ex: Uma linha de produção está sendo
analisada para efeito de controle de
qualidade das peças produzidas. A
produção é interrompida para regulagem
toda vez que uma peça defeituosa é
encontrada.

36. • Uma v.a. X tem distribuição Geométrica
de parâmetro p (probabilidade de
sucesso) se sua função de probabilidade
é dada por:
P( X  x)  p(1  p) , 0  p  1, x  0,1,2,....
x
1 p 1 p
E( X )  , Var ( X )  2
p p

37. Hipergeométrica
• É adequada quando consideramos
extrações casuais feitas sem reposição de
uma população dividida segundo dois
atributos.
• Ex: Em problemas de controle de
qualidade, lotes com N itens são
examinados e divididos em dois grupos:
defeituosos e não defeituosos.

38. • Considere um conj. de n objetos dos quais m são do
tipo I e n-m são do tipo II. Para um sorteio de r objetos
(r<n) ao acaso e sem reposição, defina X com o número
de objetos do tipo I.
• Uma v.a. X tem distribuição hipergeométrica se sua
função de probabilidade é dada por:
 m  n  m 
 
 x  r  x 

P( X  x)     , x  0,1,..., min( r , m)
n
 
r
 
rm rm(n  m)(n  r )
E( X )  , Var ( X ) 
n n 2 (n  1)