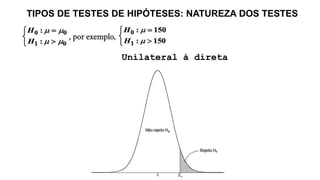
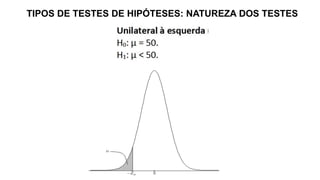
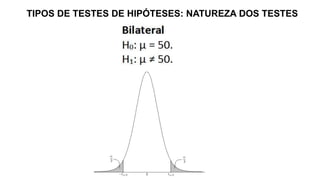
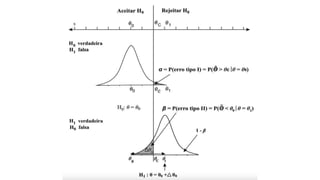
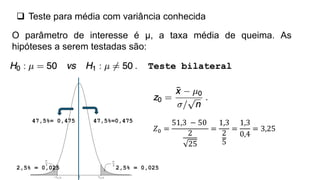
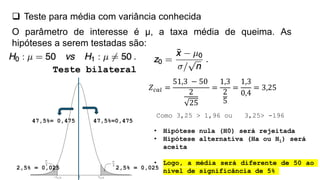
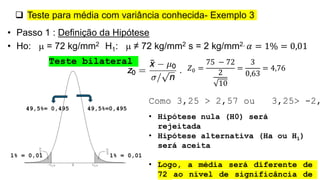
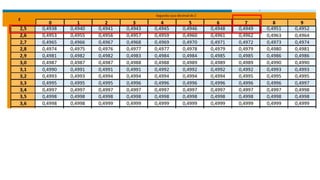
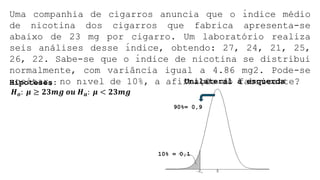
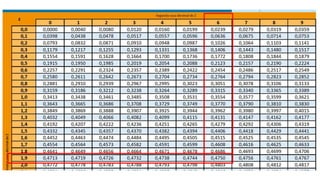
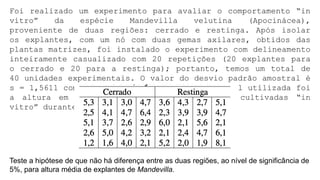
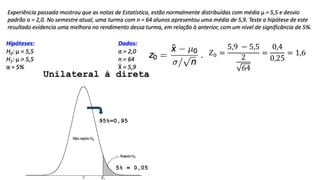
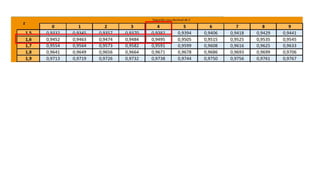
O documento aborda conceitos fundamentais sobre hipóteses estatísticas, incluindo definições de hipótese nula e alternativa, tipos de testes e métodos de validação estatística. Exemplos práticos ilustram a aplicação de testes para médias com variâncias conhecidas e desconhecidas, além de discutir a importância da região crítica e a decisão estatística. Também são apresentados casos práticos de experimentos e suas análises, evidenciando a aplicação desses testes em diferentes contextos.