[1] O documento discute conceitos estatísticos como distribuição amostral, teorema do limite central e intervalos de confiança. [2] É explicado que as médias de amostras aleatórias de uma população se aproximam de uma distribuição normal e que o erro padrão da média pode estimar a precisão da média amostral. [3] O documento mostra como calcular intervalos de confiança para estimar faixas nos quais a média populacional verdadeira provavelmente se encontra.

1. Inferência Estatística:
Conceitos Básicos II
Distribuição Amostral e Teorema do Limite Central
Análise Exploratória de dados no SPSS
Vitor Vieira Vasconcelos
Flávia da Fonseca Feitosa
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Junho de 2017

2. O Que Revisamos Na Aula
Passada
 Populações e Amostras
 Medidas de Tendência Central: Média, Moda, Mediana
 Medidas de Variabilidade: Variância e Desvio Padrão
 Curva Normal
 Distribuições de Frequência e Probabilidade
 Escores padrão (valor padronizado z)
 Cálculo da probabilidade sob a curva normal
 Ambiente SPSS

3. Aula de Hoje
Conceitos Básicos de Inferência Estatística
(Continuação)
Distribuição Amostral e Teorema do Limite Central

4. Leitura de Referência
Capítulo 1
Tudo o que você sempre quis
saber sobre estatística
(bem, quase tudo)
(parcialmente, p. 42 – 47)

5. Minha Amostra é
Representativa da
População?
DISTRIBUIÇÃO
AMOSTRAL
Convenções:
μ = média população
X = média amostra
σ = DP população
s = DP amostra
Usamos amostras para estimar o
comportamento/características de uma
população. Por exemplo, usamos a
média da amostra (X), para estimar a
média da população (μ).
Se pegarmos muitas amostras de uma
mesma população, cada amostra terá
sua própria média e em várias dessas
amostras as médias serão diferentes.

6. Minha Amostra é
Representativa da
População?
Podemos construir uma distribuição de
frequência com as médias destas
amostras!
DISTRIBUIÇÃO AMOSTRAL
Distribuição de frequências das médias
de todas as amostras de uma mesma
população. Está centrada no mesmo
valor que a média da população
DISTRIBUIÇÃO
AMOSTRAL
Convenções:
μ = média população
X = média amostra
σ = DP população
s = DP amostra

7. Características de uma
distribuição amostral
DISTRIBUIÇÃO
AMOSTRAL
1. Se aproxima de uma curva normal
(desde que o tamanho da amostra seja
razoavelmente grande – N > 30)
2. A média de uma distribuição amostral
(a média das médias) é igual à
verdadeira média populacional (μ).
3. O desvio padrão de uma distribuição
amostral (σX ) é menor do que o da
população (σ). A média amostral é mais
estável do que os escores que a compõe.

8. Erro Padrão da Média
DISTRIBUIÇÃO
AMOSTRAL
ERRO PADRÃO
Mede variabilidade
entre as médias de
diferentes amostras.
Na verdade, deveria ser o desvio padrão da população dividido
pela raiz quadrada do tamanho da amostra; no entanto, para
amostras grandes, essa aproximação é razoável.
ERRO PADRÃO DA MÉDIA (σX )
Desvio padrão das médias das amostras.
Medida de quão representativa a
amostra poderá ser da população
Na realidade não podemos selecionar
centenas de amostras para construir
uma distribuição amostral.
Técnica para estimar o erro padrão a
partir do desvio padrão da amostra (s):
Dividir s pela raiz quadrada do tamanho
da amostra (N)

10. Erro Padrão da Média
RECAPITULANDO:
 Normalmente estamos interessados em utilizar a média da
amostra como uma estimativa do valor da média da
população.
 No entanto, amostras diferentes fornecerão valores
diferentes da média.
 O Erro Padrão pode ser usado para se ter uma ideia da
diferença entre a média da amostra e a média da população.
 O Erro padrão pode ser estimado  maior quando o desvio
padrão da população é maior (na falta do desvio padrão da
população, usamos o da amostra); menor quando o número
da amostra é maior.

11. Erro Padrão da Média
Além de nos fornecer uma ideia da diferença entre a média da
amostra (X) e a média da população (μ)…
 Com ajuda do Erro Padrão da Média podemos estimar a
probabilidade de nossa média populacional situar-se
realmente dentro de um intervalo de valores médios 
Conceito de INTERVALO DE CONFIANÇA

12. Intervalos de Confiança
Uma abordagem para determinar a precisão da
média da amostra:
Calcular os limites entre os quais acreditamos que o
valor da média verdadeira estará
INTERVALO DE CONFIANÇA
Gama de valores (limites) entre os quais achamos que
o valor da população (parâmetro) estará
(no caso, o valor da média verdadeira)

13. Intervalos de Confiança
Um intervalo de confiança (IC) de 95%
Como interpreto???
Se selecionarmos 100 amostras, calcularmos a
média e, depois de determinarmos o intervalo de
confiança para aquela média, 95% dos intervalos
de confiança conterão o valor real da média da
população

15. OK! Agora
vamos ver como
se calcula o IC…
DISTRIBUIÇÃO
AMOSTRAL DE
MÉDIAS
A MÉDIA DA NOSSA AMOSTRA ESTÁ EM
ALGUM PONTO DA DISTRIBUIÇÃO

16. Intervalos de Confiança
Lembram por que o valor 1,96
é um valor de z importante???
Lembrem também como
podemos converter
escores em escores-z:
escores-z
E 2,58?
E 3,29?
Porque 95% dos escores de z estão
entre -1,96 e 1,96!!!

17. 1,96-1,96

18. Intervalos de Confiança
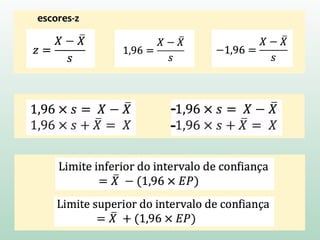
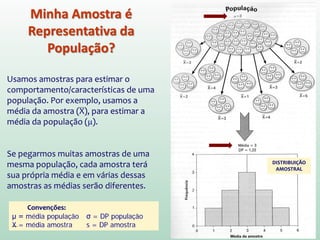
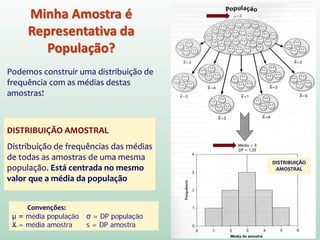
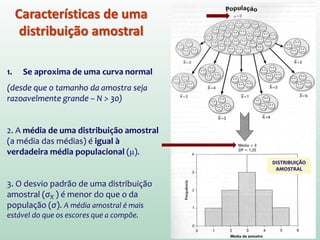
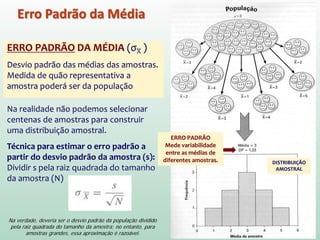
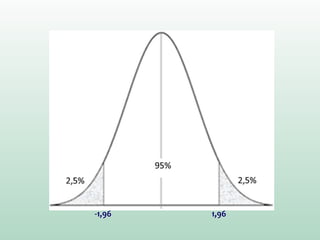
Se soubermos que nossos limites serão -1,96 e 1,96,
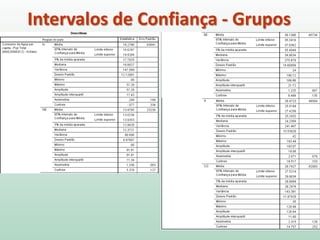
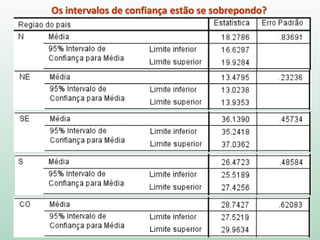
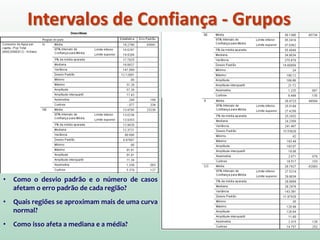
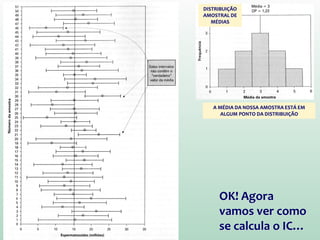
em escores-z, quais são os escores correspondentes
em valores dos nossos dados?
[É o inverso do que fizemos na última aula]
Para encontrar isso, vamos recolocar z na equação
escores-z

19. escores-z
-
-

20. escores-z
Usamos o Erro Padrão e não o Desvio
Padrão porque estamos interessados
na variabilidade das médias das
amostras e não na variabilidade das
observações dentro da amostra

21. Intervalos de Confiança

22. Exemplo – IC 95%
Digamos que tenhamos coletados dados sobre o preço do m2 dos
imóveis em um determinado bairro. Temos uma amostra de 100
imóveis (N=100), com média = 3800 e desvio padrão (s) = 1500.
Cálculo do Erro Padrão (EP):

23. Exemplo – IC 95%
Digamos que tenhamos coletados dados sobre o preço do m2 dos
imóveis em um determinado bairro. Temos uma amostra de 100
imóveis (N=100), com média = 3800 e desvio padrão (s) = 1500.
Limite inferior do intervalo de confiança = 3800 – (1,96*150) = 3506
Limite superior do intervalo de confiança = 3800 + (1,96*150) = 4094

24. Exemplo – IC 95%
Digamos que tenhamos coletados dados sobre o preço do m2 dos
imóveis no Bairro W. Temos uma amostra de 100 imóveis (N=100),
com média = 3800 e desvio padrão (s) = 1500.
Limite inferior do intervalo de confiança = 3800 – (1,96*150) = 3506
Limite superior do intervalo de confiança = 3800 + (1,96*150) = 4094
Considerando que 95% dos intervalos de confiança contém a média
da população, podemos dizer que este intervalo entre 3506 e 4094
tem 95% de chance de conter a média real do preço do m2 nos
imóveis no Bairro W.

25. Intervalos de Confiança mais Exatos
Para amostras pequenas, onde s é uma estimativa menos confiável de σ
devemos construir nosso intervalo de confiança de maneira um pouco
diferente.
Ao invés de usar 1.96 (escore-z), usamos um valor ligeiramente maior
para refletir nossa redução na confiança. Este valor é baseado na
distribuição t.

26. Relembrando a aula passada:
Variância e Graus de Liberdade
VARIÂNCIA – “média do quadrado dos desvios”
No entanto, como geralmente
queremos usar o erro na amostra para
estimar o erro na população,
dividiremos o SS pelo
nr. de observações menos 1
(graus de liberdade).
Assim, aumentamos ligeramente a
variância amostral para produzir
estimativas não tendenciosas (mais
precisas) da variância populacional
Estimativa da variância da
população usando n amostras
aleatórias xi onde i = 1, 2, ..., n.

27. Intervalos de Confiança mais Exatos
Neste caso, o escore z é substituído pela razão t.
A razão t usa uma estimativa de erro padrão baseada em dados amostrais. À
medida que o tamanho da amostra aumenta, o valor de ambas se torna
muito parecido
(…)
t(i;0,05)
gl = N-1
P = 1 – nível de confiança
(área nas extremidades da
distribuição t)

28. Comparação entre Intervalos de
Confiança
Suponha que tenhamos dois ou mais grupos separados, por
exemplo, os municípios do ABC. Podemos construir um
intervalo de confiança de 95% para a média para cada um
dos grupos, e então construir um gráfico com esses
intervalos contra um eixo comum para verificar se existe
uma interseção (i.e. se existem alguns valores em comum).
Se os intervalos não se sobrepõem, então temos (pelo
menos) 95% de confiança de que as verdadeiras médias não
são iguais.

29. Intervalos de Confiança no SPSS
1. Abra o arquivo “AguaSNIS2010.sav”
2. No SPSS, vá em Analisar> Estatísticas Descritivas > Explorar…
3. Selecione a variável “Consumo de água per capita – pop
total” e, em “Estatísticas”, selecione “Descritivas” e 95%

30. Intervalos de Confiança no SPSS
Limite inferior= 24.77 – (1,96*0.25) = 24.28
Limite superior= 24.77 + (1,96*0.25) = 25.25

31. Intervalos de Confiança no SPSS

32. Intervalos de Confiança no SPSS
Assimetria

33. Intervalos de Confiança - Grupos
1. No SPSS, vá em Analisar> Estatísticas Descritivas > Explorar…
2. Selecione a variável “Consumo de água per capita – pop
total” na lista de variáveis dependents e a variável “REGIAO”
em lista de fatores.
3. Em “Estatísticas…”, selecione “Descritivas” e 95%

34. Intervalos de Confiança - Grupos

35. Intervalos de Confiança - Grupos

36. Os intervalos de confiança estão se sobrepondo?

37. Intervalos de Confiança - Grupos
• Como o desvio padrão e o número de casos
afetam o erro padrão de cada região?
• Quais regiões se aproximam mais de uma curva
normal?
• Como isso afeta a mediana e a média?

38. Atividade
Individual:
1. Qual a diferença entre desvio padrão e erro padrão?
2. O que é um intervalo de confiança?
3. Como interpretar um intervalo de confiança de 95%?
Em grupo:
4. Preparem uma planilha com no mínimo 3 variáveis que vocês
pretendam utilizar para o trabalho da disciplina
5. Cada componente do grupo escolherá uma variável e analisará,
no SPSS: histograma, a média, intervalo de 95% de confiança para
média, erro padrão, mediana, desvio padrão, assimetria e
curtose.