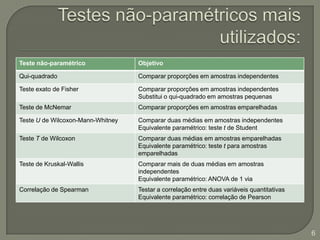
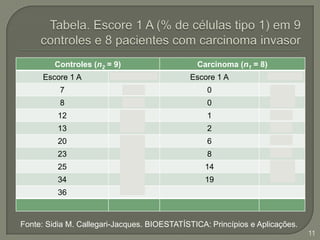
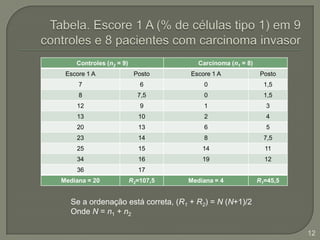
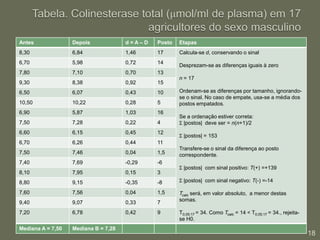
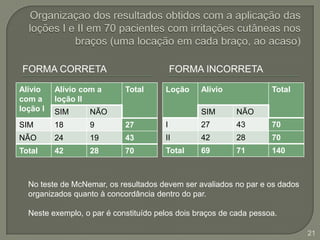
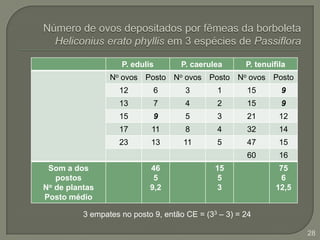
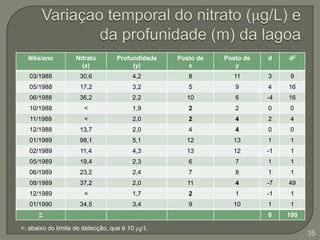
Este documento discute testes estatísticos não paramétricos alternativos aos testes paramétricos tradicionais. Apresenta os testes U de Wilcoxon-Mann-Whitney, T de Wilcoxon, de McNemar e de Kruskal-Wallis, explicando quando cada um deve ser usado e como são calculados. Também discute o coeficiente de correlação de Spearman, uma alternativa ao coeficiente de Pearson para dados não normais.