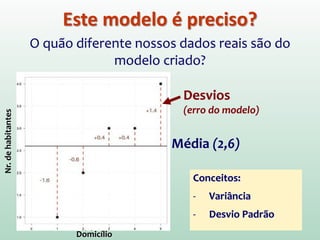
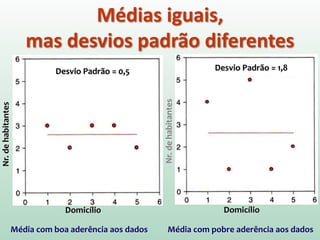
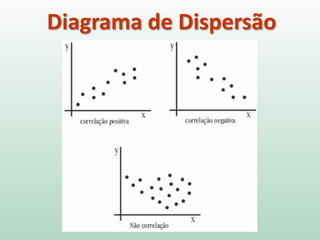
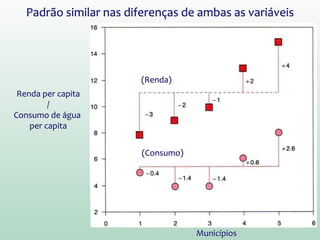
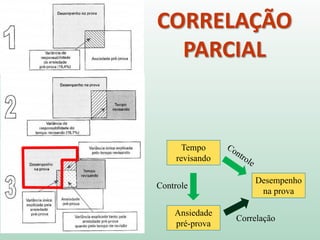
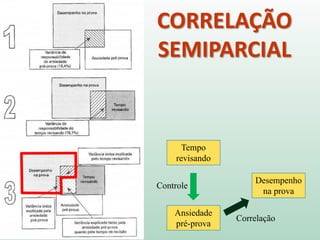
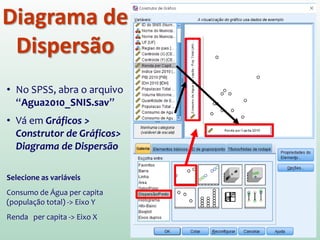
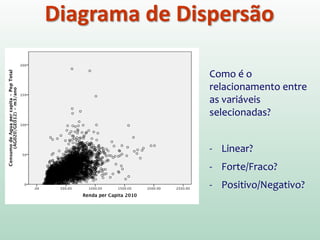
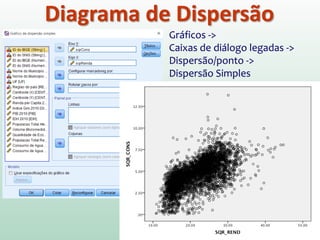
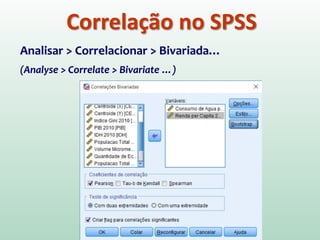
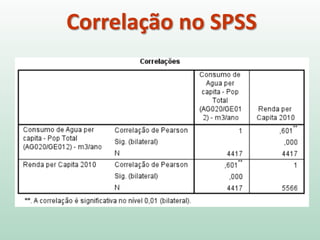
1) O documento discute o conceito de inferência estatística e como ela pode ser usada para estimar parâmetros populacionais a partir de amostras. 2) A média é apresentada como um modelo estatístico comum e como sua precisão pode ser medida pelo desvio padrão. 3) A correlação é introduzida como uma medida do relacionamento linear entre variáveis e como ela pode ser representada graficamente através de diagramas de dispersão.

1. CORRELAÇÃO
Vitor Vieira Vasconcelos
Flávia da Fonseca Feitosa
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Julho de 2017

2. Inferência Estatística: Método científico para tirar
conclusões sobre os parâmetros da população a partir
da coleta, tratamento e análise dos dados de uma
amostra recolhida dessa população.
 Estatísticas da Amostra para Estimar Parâmetros da População
Inferência Estatística se resumindo a uma equação:
Revisão
Saídai = (Modeloi) + erroi

3. Média como um modelo estatístico
Uma representação simplificada de uma
característica do mundo real:
 A média do consumo per capita de água na
Região Sudeste
 A altura média dos edifícios em São Caetano
 O PIB médio dos municípios localizados no arco
do desmatamento

4. Este modelo é preciso?
O quão diferente nossos dados reais são do
modelo criado?
Média (2,6)
Desvios
(erro do modelo)
Nr.dehabitantes
Domicílio
Conceitos:
- Variância
- Desvio Padrão

5. Média com boa aderência aos dados
Médias iguais,
mas desvios padrão diferentes
Média com pobre aderência aos dados
Nr.dehabitantes
Domicílio
Nr.dehabitantes
Domicílio
Desvio Padrão = 0,5 Desvio Padrão = 1,8

6. Para além de Médias… Modelos Lineares
 São modelos baseados sobre uma linha reta,
utilizados para representar a relação entre variáveis
 Ou seja, geralmente estamos tentando resumir as
RELAÇÕES observadas a partir de nossos dados
observados em termos de uma linha reta.
ConsumodeÁguaper
Capita(m3/dia/ano)
Renda per Capita (R$)
RELAÇÃO ENTRE
CONSUMO DE ÁGUA E
RENDA

7. CORRELAÇÃO
É uma medida do relacionamento linear
entre duas variáveis
Duas variáveis podem estar:
(a) Positivamente relacionadas  quando maior a renda, maior
o consumo de água
(b) Negativamente relacionadas  quanto maior a renda,
menor o consumo de água
(c) Não há relação entre as variáveis

8. Representando Relacionamentos Graficamente
Diagrama de Dispersão
DIAGRAMA DE DISPERSÃO: Gráfico que coloca o
escore de cada observação em uma variável contra
seu escore em outra

9. Importante começar por ele!
Diagrama de Dispersão
Nos diz se a relação entre variáveis é linear, se existem
peculiaridades nos dados que valem a pena observar (outliers) e
dá uma ideia da força do relacionamento entre as variáveis.
Exemplo de Correlação Não-Linear: Renda e proporção de domicílios próprios.
Linear Não linear Não Linear

10. Diagrama de Dispersão

11. Como medimos relacionamentos?
Veremos duas medidas para expressar
estatisticamente os relacionamentos entre
variáveis:
1. Covariância
2. Coeficientes de correlação

12. COVARIÂNCIA
Uma maneira de verificar de duas variáveis
estão associadas é ver se elas variam
conjuntamente. Ou seja, ver se as
mudanças em uma variável correspondem
a mudanças similares na outra variável
RELEMBRANDO O CONCEITO DE VARIÂNCIA:

13. COVARIÂNCIA
Em outras palavras:
Quando uma variável se desvia de sua média,
esperamos que a outra variável se desvie da sua
média de maneira similar (ou de maneira
diretamente oposta).
RELEMBRANDO O CONCEITO DE VARIÂNCIA:

14. Padrão similar nas diferenças de ambas as variáveis
Municípios
Renda per capita
/
Consumo de água
per capita
(Renda)
(Consumo)

15. Como calcular a semelhança entre o
padrão das diferenças das 2 variáveis?
Multiplicando a diferença de uma variável pela diferença
correspondente da segunda variável!
 Se ambos os erros são positivos ou negativos, isso nos dará um valor positivo
(desvios na mesma direção)
 Se um erro for positivo e outro negativo, isso nos dará um valor negativo
(desvios em direções opostas)
COVARIÂNCIA

16. Covariância
Média das Diferenças Combinadas
É uma medida de como duas variáveis variam
conjuntamente.
Se a covariância entre duas variáveis é igual a zero, significa que elas são
independentes.
COVARIÂNCIA

17. Municípios
Renda per capita
/
Consumo de água
per capita
(Renda)
(Consumo)

18. Covariância
Covariância Positiva: Quando uma variável se desvia da
média, a outra variável se desvia na mesma direção.
Covariância Negativa: Quando uma variável se desvia da
média, a outra variável se desvia na direção oposta.
COVARIÂNCIA

19. Covariância
UM PROBLEMA!!!
A covariância depende das escalas de medida. Não é
uma medida padronizada.
Ou seja, não podemos dizer se a covariância é
particularmente grande ou pequena em relação a outro
conjunto de dados a não ser que ambos os conjuntos
fossem mensurados nas mesmas medidas.

20. Padronização &
Coeficiente de Correlação
Para superar o problema da dependência das escalas de
medida, precisamos converter a variância em um
conjunto padrão de unidades  Padronização
Precisamos de uma unidade de medida na qual qualquer
escala de mensuração possa ser convertida
Unidades de Desvio Padrão
(medida da média dos desvios a partir da média)

21. Padronização &
Coeficiente de Correlação
O COEFICIENTE DE CORRELAÇÃO
é uma covariância padronizada
COEFICIENTE DE CORRELAÇÃO DE PEARSON

22. Coeficiente de Correlação
Padronizando a covariância, encontramos um
valor que deve estar entre -1 e +1
r = +1  duas variáveis estão perfeitamente
correlacionadas de forma positiva (se uma aumenta, a outra
aumenta proporcionalmente)
r = -1  relacionamento negativo perfeito (se uma
aumenta, a outra diminui em valor proporcional
r = 0  indica ausência de relacionamento linear

23. Mas… Como saber se a
correlação não se deve a um
erro amostral, ao acaso?
Como saber se a correlação é
estatisticamente significativa?
Uma breve revisão sobre
TESTES DE HIPÓTESE

24. Para testar a significância de uma medida de
correlação, estabelecemos uma hipótese
(nula) de nenhuma correlação existe na
população.
HIPÓTESES
Hipótese Experimental (H1)  Geralmente
corresponde a uma “previsão” feita pela pesquisador
(existe uma correlação na população)
Hipótese Nula (H0)  O efeito previsto não existe
(não existe uma correlação na população)
Tornou-se convenção na análise estatística iniciar o estudo pelo
teste da hipótese nula.

25. Para confirmar ou rejeitar nossas
hipóteses:
Calculamos a probabilidade de que o efeito
observado (no nosso caso, a correlação) ocorreu
por acaso: À medida que a probabilidade do
“acaso” diminui, confirmamos que a hipótese
experimental é correta e que a hipótese nula pode
ser rejeitada.

26. E quando podemos considerar que um resultado é
genuíno, ou seja, não é fruto do acaso?
Há sempre um risco de considerarmos um
efeito verdadeiro, quando, de fato, não o
é (ERRO TIPO I). Para Ronald Fisher,
somente quando a probabilidade de algo
acontecer por acaso é igual ou menor a 5%
(<0,05), podemos aceitar que é um
resultado estatisticamente significativo.
O valor da probabilidade de cometer um
erro do tipo I num teste de hipóteses é
conhecido como NÍVEL DE SIGNIFICÂNCIA e
é representado pela letra α
Os níveis de significância mais utilizados são de 5%, 1% e 0,1%

27.  Para estabelecer se um modelo (no caso, a medida de
correlação) é uma representação razoável do que está
acontecendo, geralmente calculamos uma ESTATÍSTICA
TESTE
 É uma estatística que tem propriedades conhecidas, já
sabemos a frequência com que diferentes valores desta
estatística ocorrem.
 Sabemos suas distribuições e isso nos permite, uma vez
calculada a estatística teste, calcular um valor tão grande
como o que temos. Se temos uma estatística teste de 100,
por exemplo, poderíamos então calcular a probabilidade
de obter um valor tão grande.
Estatísticas teste

28. Estatísticas teste
Existem várias estatísticas testes (t, F…).
Entretanto, a maioria delas representa o seguinte:
A forma exata desta equação muda de teste pra teste.
Se nosso modelo é bom, esperamos que a variância explicada
por ele seja maior do que a variância que ele não pode explicar.

29. Quanto maior a estatística teste, menor a probabilidade
de que nossos resultados sejam fruto do acaso.
Quando esta probabilidade cai para abaixo de 0,05
(Critério de Fisher), aceitamos isso como uma confiança
suficiente para assumir que a estatística teste é assim
grande porque nosso modelo explica um montante
suficiente de variações para refletir o que realmente
está acontecendo no mundo real (a população)
Estatísticas teste

30. Quanto maior a estatística teste, menor a probabilidade
de que nossos resultados sejam fruto do acaso.
Ou seja,
Rejeitamos nossa hipótese nula e aceitamos nossa
hipótese experimental
Estatísticas teste

31. Hipótese Nula Hipótese Experimental
Estatísticas teste
REJEITA!

32. Teste de Significância do r de Pearson
Para testar a significância do r, calculamos uma estatística
teste conhecida como “razão t”, com graus de liberdade
igual a N-2.
Olhar na tabela o valor crítico de t, com graus de liberdade
“N-2” e α=0,05
Se tcalculado > tcrítico, podemos rejeitar a hipótese nula de que
ρ=0.

33. Teste de Significância do r de Pearson
Para testar a significância do r, calculamos uma estatística
teste conhecida como “razão t”, com graus de liberdade
igual a N-2.
Olhar na tabela o valor crítico de t, com graus de liberdade
“N-2” e α=0,05
Se tcalculado > tcrítico, podemos rejeitar a hipótese nula de que
ρ=0.
O que o modelo “explica”
O que o modelo NÃO “explica”
N maior, estatística maior

34. Hipótese Direcional: “Existe uma correlação
populacional positiva”
 TESTE DE HIPÓTESE UNILATERAL
Hipótese Não Direcional: “Existe uma correlação
populacional positiva ou negativa”
 TESTE DE HIPÓTESE BILATERAL
Testes Uni e Bilaterais

35. Testes Uni e Bilaterais
Valor-p (p-value): Probabilidade de se obter uma estatística teste igual ou mais
extrema que aquela observada em uma amostra, sob hipótese nula. Ou seja, pode-
se rejeitar a hipótese nula a 5% caso o valor-p seja menor do que 0,05.
Valor-p ≠ nível de significância (α). O nível de significância é estabelecido antes da
coleta dos dados. Já o valor-p é obtido de uma amostra.
Unilateral UnilateralBilateral

37. 1. Escolhemos as hipóteses nula (Ho) e alternativa (H1)
2. Decidimos qual será a estatística utilizada para testar a
hipótese nula (no nosso exemplo, a estatística t)
3. Estipulamos o nível de significância (α), ou seja, um
valor para o erro do tipo I. Com este valor, construímos
a região crítica, que servirá de regra para rejeitar ou
não a hipótese nula.
4. Calculamos o valor da estatística teste
5. Quanto o valor calculado da estatística NÃO pertence à
região crítica estabelecida pelo nível de significância,
NÃO rejeitamos a hipótese nula. Caso contrário,
rejeitamos a hipótese nula.
Passo-a-Passo: Teste de Hipótese

38. Exigências para o uso do coeficiente
de correlação r de Pearson
1. Relação Linear entre X e Y
2. Dados intervalares
3. Amostragem Aleatória (assim podemos aplicar
o teste de significância)
4. Características normalmente distribuídas
(importante quando se testa significância em
amostras pequenas - N<30)

39. Um alerta sobre interpretação:
CAUSALIDADE
Coeficientes de correlação NÃO dão indicação
da causalidade
1. O problema da terceira variável
Em qualquer correlação bivariada, a causalidade
entre duas variáveis não pode ser dada por
certo, porque podem ter outras variáveis,
medidas ou não, afetando os resultados

40. Sorvete e Afogamentos, 2006
Consumo de Sorvete
Mortesporafogamento
Verão
Consumo de
sorvete
AfogamentoCorrelação
CausaCausa

41. Um alerta sobre interpretação:
CAUSALIDADE
Coeficientes de correlação NÃO dão indicação
da causalidade
2. Direção da causalidade
Coeficientes de correlação nada dizem sobre qual
variável causa a alteração na outra. Mesmo se
pudéssemos ignorar o problema da terceira variável, e
pudéssemos assumir que as duas variáveis
correlacionadas eram as únicas importantes, o
coeficiente de correlação não indica em qual direção a
causalidade opera.

42. Um alerta sobre interpretação:
CAUSALIDADE
Coeficientes de correlação NÃO dão indicação
da causalidade
2. Direção da causalidade
ou

43. Para diversão
Spurious Correlation – www.tylervigen.com

46. Utilizando o R2 para Interpretação
Embora não possamos tirar conclusões diretas
sobre causalidade, podemos levar o coeficiente de
correlação um passo a frente elevando-o ao
quadrado  Coeficiente de Determinação, R2
O Coeficiente de Determinação é uma medida
da quantidade de variação em uma variável que
é explicada pela outra.
Quanto da variabilidade do consumo de água per
capita pode ser “explicada” pela renda per capita?

47. CORRELAÇÃO BIVARIADA
Coeficientes
1. COEFICIENTE DE CORRELAÇÃO DE PEARSON
2. COEFICIENTE DE CORRELAÇÃO DE
SPEARMAN  NÃO PARAMÉTRICO – Pode
ser usada quando dados violarem suposições
paramétricas, tais como dados não normais,
dados ordinais.
3. TAU DE KENDALL  NÃO PARAMÉTRICO.
Adequado para conjunto pequeno de dados
com muitos escores “empatados”

48. CORRELAÇÃO PARCIAL
Até o momento tratamos da CORRELAÇÃO
BIVARIADA: correlação entre 2 variáveis. Exemplos:
coeficiente de correlação de Pearson (r) e o de
Spearman
Mas…
Nossa interpretação da relação entre duas
variáveis muda de alguma maneira ao
olharmos para o contexto mais amplo de
outros fatores relacionados???

49. CORRELAÇÃO PARCIAL
Em muitos casos, é importante ver o
relacionamento entre duas variáveis quando o
efeito de outras variáveis são constantes.
CORRELAÇÃO PARCIAL: determina o
relacionamento entre variáveis
“controlando” o efeito de uma ou mais
variáveis.

50. CORRELAÇÃO
PARCIAL
Desempenho
na prova
Tempo
revisando
Ansiedade
pré-prova
Controle
Correlação

51. CORRELAÇÃO
SEMIPARCIAL
Desempenho
na prova
Tempo
revisando
Ansiedade
pré-prova
Controle
Correlação

52. Análise de Correlação
no SPSS

53. • No SPSS, abra o arquivo
“Agua2010_SNIS.sav”
• Vá em Gráficos >
Construtor de Gráficos>
Diagrama de Dispersão
Selecione as variáveis
Consumo de Água per capita
(população total) -> Eixo Y
Renda per capita -> Eixo X
Diagrama de
Dispersão

54. Diagrama de Dispersão
Como é o
relacionamento entre
as variáveis
selecionadas?
- Linear?
- Forte/Fraco?
- Positivo/Negativo?

55. Diagrama de Dispersão
Gráficos ->
Caixas de diálogo legadas ->
Dispersão/ponto ->
Dispersão Simples

56. Correlação no SPSS
Analisar > Correlacionar > Bivariada…
(Analyse > Correlate > Bivariate …)

57. Correlação no SPSS

58. ATIVIDADE 4
Utilizando os dados do seu trabalho de curso,
conduza as seguintes análises no SPSS:
1. Construa e interprete diagrama(s) de dispersão a
partir de variáveis de interesse.
2. Calcule e interprete a correlação entre variáveis
de interesse. É significativa? O que isso significa?
O exercício deverá ser compreendido como uma versão
preliminar de parte do trabalho final da disciplina.
Interprete. Aproveite para entender melhor o problema
investigado.