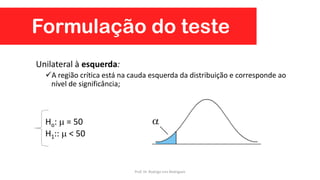
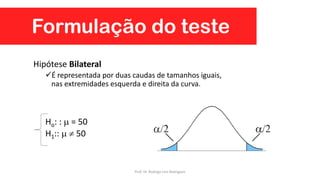
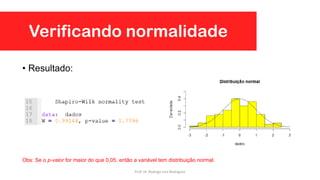
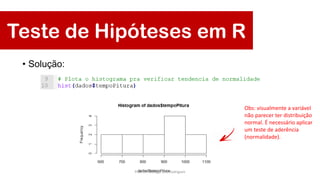
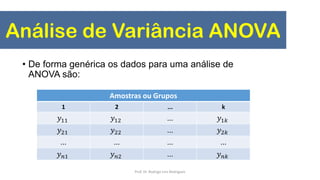
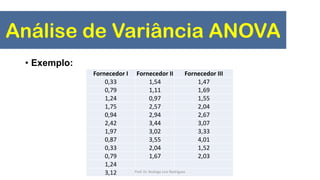
Este documento apresenta uma aula sobre testes de hipóteses e ANOVA. Inclui introdução sobre testes de hipóteses, formulação de hipóteses, etapas para construção de hipóteses, testes de normalidade, teste t de Student para uma, duas amostras e amostras pareadas e Análise de Variância (ANOVA).