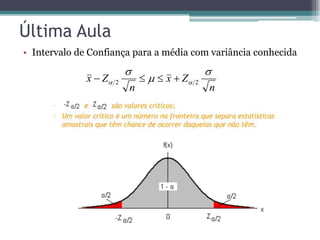
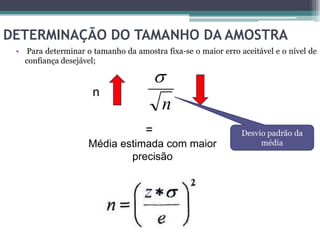
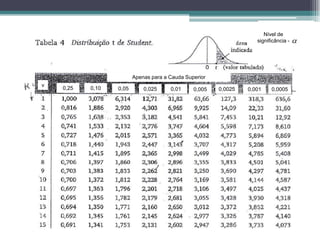
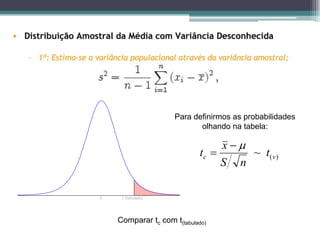
Este documento resume a última aula de bioestatística sobre testes de hipóteses. Ele explica como calcular intervalos de confiança para a média com variância conhecida e desconhecida usando as distribuições normal e t-Student. Também descreve o procedimento geral para testes de hipóteses, incluindo como definir as hipóteses nula e alternativa, escolher uma estatística de teste, fixar o nível de significância e tomar uma decisão sobre rejeitar ou não a hipótese nula.

1. Aula 5 : Bioestatística
Caroline Godoy
Turma: Graduação em Educação Física

2. Última Aula
• Intervalo de Confiança para a média com variância conhecida
 
x  Z 2    x  Z 2
n n

3. DETERMINAÇÃO DO TAMANHO DA AMOSTRA
• Para determinar o tamanho da amostra fixa-se o maior erro aceitável e o nível de
confiança desejável;

n
n
= Desvio padrão da
Média estimada com maior média
precisão

4. DISTRIBUIÇÃO t - Student
• Vimos a distribuição Normal e suas características. Veremos agora a distribuição t–Student:
• Características: - Simétrica, semelhante a distribuição Normal, porém com caudas mais
largas, ou seja, pode gerar valores mais extremos do que uma Normal;
- Vimos que uma variável X (característica de estudo) com distribuição
normal pode ser caracterizada como: X ~ N(µ ; σ2); já para uma variável X com distribuição
t-Student, esta poderia ser caracterizada como X ~ t-Student (v) onde v é o número de graus
de liberdade em relação à amostra que pode ser calculado como número de valores
observados menos o número de amostras retiradas da população, ou seja, se temos n valores
em 1 amostra, temos o grau de liberdade como n-1.
• A distribuição de probabilidade é:
• Como é uma distribuição muito usada, os valores são tabelados assim como a Normal.

5. Nível de
significância - 
Apenas para a Cauda Superior
v
0,25 0,10 0,05 0,025 0,01 0,005 0,0025 0,001 0,0005

6. Para definirmos as probabilidades
olhando na tabela:
x
tc  ~ t( v )
S n
0 t (tabulado)
Comparar tc com t(tabulado)

7. -tα/2 tα/2
ou
S S
x  t 2    x  t 2
n n

8. DISTRIBUIÇÃO t - Student
• Usa-se os cálculos da t-Student para calcular as probabilidades quando:
1. O valor da amostra é pequeno;
2. Não conhecemos a variância da população.

10. Testes de Hipóteses

11. Conceitos
• Vimos que podemos tirar informações dos parâmetros de uma de uma
população através de uma amostra, porém na maioria das vezes
precisamos comparar esses valores com outros já pré-estabelecidos;
• Para isso existem os testes de hipóteses que fornecem uma metodologia
para verificar se os dados amostrais trazem evidências que apoiam ou não
uma hipótese formulada.

12. Conceitos - Exemplo
Hipótese Científica:
H0: O novo medicamento não é melhor que o medicamento
H1: tradicional.
O novo medicamento é melhor que o medicamento tradicional.

13. Conceitos - Exemplo
n
Variável de interesse
Hipótese Estatística:
H0: p≤0,4 (O medicamento novo não é melhor que o tradicional)
H1: p>0,4 (O medicamento novo é melhor que o tradicional)

14. Conceitos - Exemplo
• Regra de decisão:
Rejeita H0 se Y ≥ 9
Não rejeita H0 se Y < 9
• Testar uma hipótese estatística significa estabelecer uma
regra que nos permita, com base na informação da
amostra, decidir pela rejeição ou não de H0.
• Região de Rejeição ou Região Crítica
RC = {9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20} :
região crítica
RCc = {0, 1, 2, 3, 4, 5, 6, 7, 8}: região de aceitação de H0

15. Conceitos - Exemplo
• Na decisão pela rejeição ou não da hipótese nula pode-se
cometer 2 tipos de erros:
Decisão Situação na população
baseada na
amostra H0 Verdadeira H0 Falsa
Aceitar H0 Decisão correta Erro Tipo II
Rejeitar H0 Erro Tipo I Decisão correta
• Erro Tipo I: Dizer que o medicamento novo é melhor que
o tradicional, quando na verdade não é;
• Erro Tipo II: Dizer que o medicamento novo não é melhor
que o tradicional, quando na verdade é melhor.

16. Conceitos - Exemplo
• O maior valor do erro tipo I é chamado de nível de
significância de um teste (prob. máxima que aceitamos de
ocorrer o risco do erro), denotado por:
  P(erro tipo I )  P(rejeitar H0 | H0 é verdadeira)
• A probabilidade de ocorrer o erro tipo II é denotada por:
  P(erro tipo II )  P(não rejeitar H0 | H0 é falsa)
• Em geral, o erro tipo I é mais sério que o erro tipo II,
portanto escolhe-se controlar  e escolhe-se um teste tal
que  seja o menor possível.

17. Procedimento Geral do Teste de Hipóteses
• Passo 1: Fixar qual hipótese H0 a ser testada e qual a alternativa H1;
• Passo 2: Use a teoria estatística e as informações disponíveis para
decidir qual estatística (estimador será usada para testar H1;
• Passo 3: Fixar a probabilidade α de cometer o erro tipo I e usar este
valor para construir a região de decisão;
• Passo 4: Usar as observações da amostra para calcular o valor da
estatística de teste;
• Passo 5: Se o valor da estatística calculado com os dados da
amostra pertencer à região de decisão não rejeite H0, cc rejeite.

18. Exercício 1 – teste de hipótese para a média
com σ2 conhecida
• Uma máquina automática para encher pacotes de café enche-os
segundo uma distribuição normal, com média μ e variância sempre
igual a 400 g2. A máquina foi regulada para μ=500 g. Desejamos,
periodicamente verificar se a produção está sob controle, isto é, se
μ=500 g ou não. Se uma dessas amostras apresentasse uma média
de 492 g, você pararia ou não a produção para regular a máquina?
n=16
H0 :   0 Rejeita-se H0 se
i ) H1 :   0
X 
Estatística de teste => zc  ~ N (0;1) ii) H1 :   0

n iii) H1 :   0
Livro

19. Exercício 2 - teste de hipótese para a média
com σ2 conhecida
• Um pesquisador deseja estudar o efeito de certa substância no tempo
de reação de seres vivos a certo estímulo. Um experimento é
realizado em 10 cobaias, que são inoculadas com substância e
submetidas a um estímulo elétrico, com seus tempos de reação (em
segundos) anotados. Admita que o tempo de reação segue, em geral,
o modelo normal, com média, com média de 8 segundos e desvio
padrão 2 segundos. O pesquisador desconfia, entretanto, que o
tempo médio sofre alteração por influencia da substância. Determine
a região crítica considerando α=0,06;
• Encontre a probabilidade do erro tipo II;

20. Poder de um teste
• Avaliamos o desempenho de um intervalo de confiança de duas
maneiras:
• Por seu nível de confiança, que informa com que frequência o
método é bem sucedido em capturar o parâmetro verdadeiro;
• Por sua margem de erro que nos diz quão sensível o método é,
ou seja, quão próximo o intervalo acerta o parâmetro sendo
estimado.
• Ou pelo poder do teste
1   ( )  P(rejeitar H0 | H0 falso)
Probabilidade de
rejeitar dado que é
falso

21. Exercício 3 – teste de hipótese para a média
com σ2 conhecida
• Fabricantes de refrigerantes testam novas receitas para verificar a
perda de doçura durante o armazenamento. Provadores treinados
classificam a doçura antes e depois do armazenamento. A seguir
estão as perdas de doçura (doçura antes menos doçura depois do
armazenamento) encontradas por 10 provadores para uma nova
receita de refrigerante:
2,0 0,4 0,7 2,0 -0,4 2,2 -1,3 1,2 1,1 2,3
• Esses dados são uma boa evidência de que os refrigerantes
perderam a doçura? Faça as suposições necessárias.
Rejeita-se H0 se
H0 :   0
i ) H1 :   0
X 
Estatística de teste => tc 
S
~ t  Student 1
n ii) H1 :   0
n iii) H1 :   0

22. Próxima Aula
• Comparação de duas médias;
• Regressão linear.