Este documento resume os principais conceitos de variáveis aleatórias, incluindo: 1) a definição de variável aleatória e sua notação; 2) variáveis aleatórias discretas e contínuas; 3) funções de probabilidade e repartição; 4) medidas de posição como média; e 5) medidas de dispersão como variância e desvio padrão. O documento fornece exemplos para ilustrar cada um desses conceitos.
















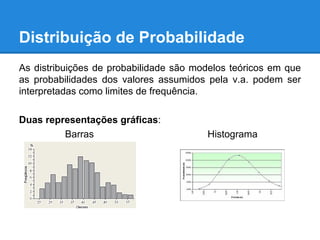





![Densidade de Probabilidade
Exemplo:
Seja X a variável diâmetro (em mm) de frutos de
mamão colhidos no estado inicial, cuja função de x
[f(x)] é dada por:
Dada a função desta variável, calcule k de modo que
f (x) seja uma f.d.p.](https://image.slidesharecdn.com/trabalho-probabilidadeeestatstica-160903014742/85/Probabilidade-e-estatistica-Variaveis-Aleatorias-25-320.jpg)



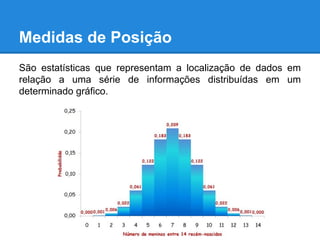




![Medidas de Posição
Exemplo.: Seja X a variável diâmetro (em mm) de frutos de
mamão colhidos no estado inicial, cuja função de x [f(x)] é dada
por:
Tem-se que:](https://image.slidesharecdn.com/trabalho-probabilidadeeestatstica-160903014742/85/Probabilidade-e-estatistica-Variaveis-Aleatorias-34-320.jpg)






![Medidas de Dispersão
Exemplo.: Seja X a variável diâmetro (em mm) de frutos de
mamão colhidos no estado inicial, cuja função de x [f(x)] é dada
por:
Tem-se que:](https://image.slidesharecdn.com/trabalho-probabilidadeeestatstica-160903014742/85/Probabilidade-e-estatistica-Variaveis-Aleatorias-41-320.jpg)


![Medidas de Dispersão
Exemplo (variável aleatória continua).: Seja X a variável
diâmetro (em mm) de frutos de mamão colhidos no estado
inicial, cuja função de x [f(x)] é dada por:
Tem-se que:](https://image.slidesharecdn.com/trabalho-probabilidadeeestatstica-160903014742/85/Probabilidade-e-estatistica-Variaveis-Aleatorias-44-320.jpg)
![Referências
[1] MONTGOMERY, Douglas C; RUNGER, George C. Estatística aplicada e
probabilidade para engenheiros. 4. ed Rio de Janeiro: LTC, 2009 493 p.
http://pt.slideshare.net/neudesmaira/estatstica-aplicada-informtica?qid=fe20f865-3a32-4d
99-802a-401b07cdb021&v=default&b=&from_search=12
http://pt.slideshare.net/cursoraizes/estatistica-aplicada-a-administracao-aula-6?qid=fe20f
865-3a32-4d99-802a-401b07cdb021&v=default&b=&from_search=6
http://www.somatematica.com.br/emedio/probabilidade.php
http://pt.scribd.com/doc/32600975/Apostila-5-Variaveis-aleatorias](https://image.slidesharecdn.com/trabalho-probabilidadeeestatstica-160903014742/85/Probabilidade-e-estatistica-Variaveis-Aleatorias-45-320.jpg)