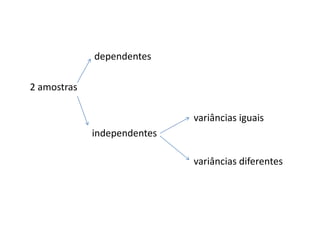
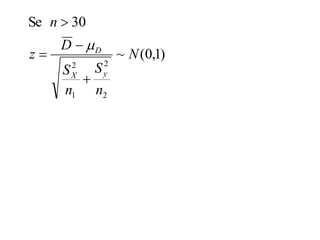Este documento descreve testes estatísticos para comparar duas médias amostrais, discutindo casos de amostras dependentes e independentes, com variâncias iguais ou diferentes. É apresentado um exemplo completo ilustrando o teste t para amostras dependentes e o teste t para amostras independentes com variâncias iguais.

1. Teste de hipóteses para
comparação de duas médias

2. Comparação de duas médias
• Objetivo: Comparar as médias amostrais de
duas populações.
• 1º passo: Verificar se as variáveis estão ou não
relacionadas.
• 2º passo: Considerar a variabilidade associada
aos valores populacionais e amostrais.

3. dependentes
2 amostras
variâncias iguais
independentes
variâncias diferentes

4. Amostras dependentes (teste t-pareado)
• São comparadas duas médias populacionais sendo
que, para cada unidade amostral, realizou-se duas
medições da característica de interesse.
Correspondem a medidas tomadas antes e após uma
dada intervenção.
• Ex: Uma distribuidora de combustíveis deseja verificar se
um novo tipo de gasolina é eficaz na revitalização de
motores velhos. Selecionou-se 12 automóveis de um
mesmo modelo com mais de 8 anos de uso e, após
regulagem dos motores, verifica-se o consumo de
combustível. Em seguida, o carro é abastecido com o
novo tipo de combustível durante 15 semanas e uma
nova aferição é feita.

5. • Como o desempenho dos automóveis foi
medido antes e depois das 15 semanas, é
razoável assumir que exista alguma
dependência entre as variáveis.
• Essa é a típica situação que o teste t-pareado
deve ser utilizado.
• As medidas tomadas antes e após a
intervenção realizada serão representadas
pelas v.a.s Xi e Yi.
• O efeito produzido pelo i-ésimo indivíduo,
pode ser representado pela variável Di= Yi - Xi.

6. • Supondo, para i=1,...,n, “ASSUMIMOS”, por
hipótese, que:
Di ~ N(D ,2D)
Queremos testar as hipóteses:
H0: A intervenção não produz efeito (D = 0)
Ha: A intervenção produziu algum efeito (D  0)
A hipótese alternativa também pode ser
unilateral!!!!

7. • O parâmetro D é estimado pela média amostral de
D e sua variância é estimada por:
n
1
S 
2
D  ( Di  D ) .
n  1 i 1
2
• O teste de hipóteses é realizado utilizando-se a
quantidade :
D  D
t
SD
n
• Que sob H0, segue uma distribuição t-Student com n-
1 graus de liberdade.

8. • Valores observados para os 12 automóveis:
Autom. 1 2 3 4 5 6 7 8 9 10 11 12
Após (Y) 11,6 8,8 9,9 9,5 11,6 9,1 10,6 10,8 13,4 10,6 10,5 11,4
Antes (X) 8,1 7,9 6,8 7,8 7,6 7,9 5,7 8,4 8,0 9,5 8,0 6,8
D=Y-X 3,5 0,9 3,1 1,7 4,0 1,2 4,9 2,4 5,4 1,1 2,5 4,6
• A média e a variância amostrais de D são:
Dm=2,9 e S2=2,4.
• 1º Passo: Definir as hipóteses nula e alternativa:
H0: D = 0 (O novo combustível não aumenta o rendimento)
Há: D > 0 (o novo combustível aumenta o rendimento)

9. • 2 Passo: Definir a região crítica com base na
hipótese alternativa:
Teste unilateral, RC:{xR|x>xc}
• 3 Passo: Identificar a distribuição do
estimador e encontrar a estimativa:
D
d i
n
Por “HIPÓTESE”, tem-se: D~N(D , 2D/n)
• 4 Passo: Fixar  e determinar a região crítica.
=5%  t=1,796

10. xc  0
tc 
2,4
12
RC={x  : x>0,80}
2,4
xc  0  1,796
12
xc  0,80
• 5 Passo: Conclusão
Como Dobs = 2,9 e Dobs>0,80, rejeitamos H0 e
concluímos que o novo combustível é eficaz
na melhora do rendimento.

11. Amostras independentes
Variâncias IGUAIS
• Geralmente não se tem informações a respeito do
valor das variâncias das populações. Entretanto,
alguns processos nos levam a crer que, apesar de
desconhecidas, as variâncias são iguais para duas
populações.
• Ex.: Digitadores são treinados em uma empresa em duas
turmas distintas. Na primeira (TURMA J) utiliza-se um método
japonês, na segunda (TURMA A) utiliza-se um método
alemão. Deseja-se comparar os dois métodos. Foram
escolhidas duas amostras aleatoriamente (uma de cada
turma) e mediu-se o tempo gasto na realização de uma tarefa
para cada aluno.

12. • Apesar de não conhecidas, as variâncias
populacionais para as duas turmas são consideradas
iguais com base em estudos anteriores.
• Os dados obtidos foram:
Turma Tempos (min)
J 10 13 9 10 14 13 10 15 12 10 9 10 13 14
A 15 12 18 16 15 17 17 15 16 17 11 17 14
• Formalizando o problema temos:
• Supomos que os dados apresentados para as turmas
J e A são variáveis aleatórias independentes (X1,...,Xn)
e (Y1,...Yn), respectivamente e que seguem a
distribuição Normal.

13. • Portanto
Xi ~ N(X, 2), i= 1, 2, ..., n1
Yj ~ N(Y, 2), j= 1, 2, ..., n2
OBS: Para ambas as populações temos a mesma
variância (desconhecida!!!)
Queremos testar se existe diferença entre o tempo
médio de digitação dos dois métodos, ou seja:
H0: X = Y
Ha: X  Y ou (Ha: X < Y | Ha: X > Y)

14. • Testar se as médias populacionais são iguais é
equivalente a testar se a diferença entre elas é
“estatisticamente” igual a 0.
• Logo podemos reescrever as hipóteses em
termos de D = X - Y
H0: D = 0
Ha: D  0 ou (Ha: D < 0 | Ha: D > 0)
Desta forma usaremos o estimador (intuitivo)
D=X-Y

15. • Do TLC tem-se que se n>30
  2
   
2
X ~ N   X ,  e Y ~ N  Y , 

 n1 

 n2 

• Se n30 usaremos a distribuição t-Student !!!
• Como as amostras são independentes:
E(D) = E(X-Y) = E(X + (-1)Y) = E(X) + (-1)E(Y) = E(X) - E(Y)
= X - Y
Var(D) = Var(X-Y) = Var(X + (-1)Y) = Var(X) + Var(-1Y) =
2 2
Var(X) + (-1)2Var(Y) = Var(X) + Var(Y) = 
n1 n2

16. • Como X e Y têm distribuição normal (se n>30)
então:
   2  2 
D ~ N   X  Y , 
n  

  1 n2  

• Se n  30 usa-se a distribuição t–Student
(cuidado com os graus de liberdade!!!)
• Como 2 é desconhecida, precisará ser
estimada. Como SX2 e SY2 são estimadores não
viciados dessa variância, usaremos como
estimativa para 2 uma combinação deles
dada por:

17. S 
2 (n1  1) S  (n2  1) S
2
X
2
Y

 ( X i  X ) 2  (Y j  Y ) 2
(n1  1)  (n2  1) n1  n2  2
C
SC2 é uma média ponderada entre SX2 e SY2 e é um
estimador não viciado!!!
Se n30
D  (  X  Y )
t ~ t( n1  n2 2)
2
S C
n1  n2

18. • Logo
=P(Rejeitar H0|H0 verd) = P(t<-tc ou t>tc|H0)
tc é obtido pela tabela da distribuição t-Student com
n1+n2 -2 graus de liberdade.
A região crítica será dada por:
RC={tR|t<-tc ou t>tc}
Obtidas as amostras, substituindo as estimativas de D e
Sc na expressão de t, obtém-se o valor tobs.
• Rejeita-se H0 se tobs pertencer à região crítica.

19. Se n>30
D  (  X  Y )
z ~ N (0,1)
2
SC
n1  n2
Então
=P(Rejeitar H0|H0 verd) = P(z<-zc ou z>zc|H0)
zc é obtido pela tabela da distribuição Normal (0,1)
A região crítica será dada por:
RC={zR|z<-zc ou z>zc}

20. Obtidas as amostras, substituindo as estimativas de D e
Sc na expressão de t, obtém-se o valor zobs.
• Rejeita-se H0 se zobs pertencer à região crítica.
• Voltando ao exemplo: Digitadores são treinados em uma
empresa em duas turmas distintas. Na primeira (TURMA J)
utiliza-se um método japonês, na segunda (TURMA A) utiliza-
se um método alemão. Deseja-se comparar os dois métodos.
Foram escolhidas duas amostras aleatoriamente (uma de cada
turma) e mediu-se o tempo gasto na realização de uma tarefa
para cada aluno.

21. Turma Tempos (min)
J 10 13 9 10 14 13 10 15 12 10 9 10 13 14
A 15 12 18 16 15 17 17 15 16 17 11 17 14
• As amostras forneceram os seguintes valores:
Turma J: n1=14, Xobs=11,57e SX2=4,1
Turma A: n2=13, Yobs= 15,38 e SY2= 4,3
Então:
Dobs = 11,57 – 15,38 = -3,81
(n1  1) S X  (n2  1) SY 13 * 4,1  12 * 4,3
2 2
SC 
2
  4,2
(n1  1)  (n2  1) 25

22. • Como a hipótese alternativa é bilateral e n<30, a
região crítica tem a forma:
RC={tR|t<-tc ou t>tc}.
Logo para =0,01, temos:
=P(Rejeitar H0|H0 verd) = P(t<-tc ou t>tc|H0).
Da tabela da t-Student com 25 graus de liberdade,
obtemos tc=2,787.
Então RC={tR|t<-2,787 ou t>2,787}.

23. • Usando a estatística do teste temos:
D  (  X  Y )  3,81  0
t   4,83
2
SC
4,2
n1  n2 14  13
• Como -4,83 pertence a região crítica,
concluímos que os métodos de fato diferem a
um nível de significância de 1%.

24. Amostras independentes
Variâncias DIFERENTES
• O teste para o caso com as variâncias desconhecidas
e desiguais é semelhante ao anterior, mas a
quantidade a ser usada para aceitar ou rejeitar H0 se
n30 será:
D  (  X  Y )
t ~t 
2 2
S S

X y
n1 n2

25. • Mas os graus de liberdade  são corrigidos
pela expressão:
2
 SX S 
2 2
  y
n n2 
  1 
2 2
 SX   Sy 
2 2
   
 n  n 
 1   2 
n1  1 n2  1

26. • Se n>30
D  (  X  Y )
z ~ N (0,1)
2 2
S S
X
 y
n1 n2
• A seqüência do teste é igual aos casos
anteriores.

27. RESUMO
1) Amostras relacionadas (teste t-pareado)
• Estimadores:
D
 Di SD 
2  ( Di  D ) 2
n n 1
• Estatística do teste:
Para todo n Por aprox. se n  120
D  D D  D
t ~ t( n 1) z ~ N (0,1)
2 2
S D SD
n n

28. 2) Amostras independentes com variâncias
desconhecidas e iguais
• Estimadores:
(n1  1) S X  (n2  1) SY
2 2
D  X Y SC 
2
(n1  1)  (n2  1)
• Estatística do teste:
Se n  30 Se n  30
D  D D  D
t ~ t( n1  n2  2) z ~ N (0,1)
2 2
SC SC
n1  n2 n1  n2

29. 3) Amostras independentes com variâncias
desconhecidas e desiguais
• Estimadores:
2 2
S X SY
D  X Y SD 
2

n1 n2
• Estatística do teste:
Se n  30 S 2
S 
2 2
 X
 y
n n2 
D  D   1 
t ~t  2 2
2
S 2
 SX   Sy 
2 2
SX
 y    
 n  n 
n1 n2  1   2 
n1  1 n2  1

30. Se n  30
D  D
z ~ N (0,1)
2 2
S Sy
X

n1 n2

31. Exercício: Num estudo sobre doenças infantis, desejamos
investigar se a incidência de casos de contaminação por
vermes é afetada pela idade. Dois grupos de crianças, um
com idades de 2 a 4 anos (GRUPO I) e outro, com idades
de 7 a 9 anos (GRUPO II) foram escolhidos para serem
examinados quanto à ocorrência de vermes. Os dados são
apresentados:
Grupo Amostra Proporção com Verminose
I 120 0,085
II 260 0,103
Para saber se as duas faixas etárias acima tem o mesmo
comportamento, realize um teste de hipóteses
envolvendo a proporção de crianças com verminose.
Considere =5% e variâncias iguais.