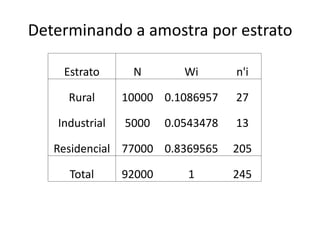
O documento discute os conceitos e métodos de amostragem para estimar parâmetros de uma população. Ele aborda como calcular o tamanho da amostra para populações finitas e infinitas, e como lidar com situações em que o desvio padrão da população é desconhecido. Além disso, explica os métodos de amostragem estratificada e como determinar o tamanho da amostra para cada estrato.

1. Planejamento da amostra

2. População infinita
Como definir o tamanho da amostra?
 z / 2
2

n
  

 
•  é o desvio padrão da população;
•  é a margem de erro ou erro amostral, isto é, a diferença
entre o resultado amostral e o verdadeiro valor
populacional, identifica a diferença máxima entre a média
amostral X e a média populacional .
• z/2 é o valor crítico que indica o grau de confiança desejado

3. E se  não for conhecido?
• Duas soluções:

1) Utiliza-se uma aproximação: 
4
 é a amplitude da variável estudada.
2) Realizar um estudo piloto, iniciando o processo de
amostragem.
Se forem coletados aleatoriamente pelo menos 31 valores
amostrais, calcular o desvio-padrão amostral S e utilizá-lo em
lugar de , neste caso utiliza-se z/2.
Se forem coletados menos de 31 valores amostrais, calcular o
desvio-padrão amostral S e utilizá-lo em lugar de , neste caso
utiliza-se t.

4. População finita
N z / 2
2 2
n
( N  1)   z / 2
2 2 2
• Em que:
• N é o tamanho da população
•  é o desvio padrão populacional
• Z/2 é o grau de confiança obtido da tabela da normal padrão
•  é o erro amostral.
Obs: Se  não for conhecido vale a proposição anterior.

5. Amostragem estratificada
• A amostragem estratificada usa informação à priori para
dividir a população em subgrupos internamente mais
homogêneos. Cada subgrupo (estrato) é então amostrado por
amostragem aleatória simples.
• Os estratos podem ser definidos com base em diversos
fatores, tais como, topografia, fronteiras políticas, estradas,
rios, características humanas, dependendo do contexto do
problema, e tendo em atenção a variabilidade daqueles
fatores em termos temporais ou espaciais.

6. Amostragem estratificada
• Seja N o número total de indivíduos na população.
• Esses N indivíduos são divididos em Li estratos de
forma que a variância dentro dos estratos é menor
que a variância da população.
• Cada estrato será composto por n’ elementos.
• Os n’ são escolhidos de acordo com um critério pré
estabelecido, tais como, tamanho dos estrados, custo
de operação, por uma margem de erro pré-
estabelecida, etc.

7. Tamanho do estrato
• Para determinar n’ de acordo com o tamanho do
estrato, primeiro determina-se uma amostra
aleatória simples (para população finita ou infinita):
 z / 2
2
N z / 2
2 2

n n
  

( N  1) 2   2 z / 2  
2
• Depois determina-se um peso para cada estrato
dado por: W  N i
i
N
• Em que Ni é o tamanho do estrato i e N é o tamanho
da população

8. Tamanho do estrato
• Determina-se n’i fazendo:
n'i  Wi n
• Se o desvio padrão da população não for conhecido,
utiliza-se os critério descritos anteriormente para
estimá-lo.

9. Exemplo
• Deseja-se estudar a renda da população da
cidade de Itajubá. Sabe-se que a população tem
92.000 habitantes e que essa população está
dividida em três áreas: rural, industrial e
residencial com 10.000, 5.000, 77.000
habitantes respectivamente. A renda da cidade
varia de R$450,00 a R$ 10.000. Qual é o
tamanho da amostra que deveremos coletar,
para que com 90% de confiança, representemos
adequadamente a renda média da população
de Itajubá? (Margem de erro R$250,00)

10. • Estimando desvio padrão:
=(10.000-450)/4= 2387,5
• População finita:
92000 * 2387,52 1,642
n  244,65
(92000  1)250  2387,5 1,64
2 2 2
• População infinita
2
 1,64 * 2387,5 
n   245,30
 250 

11. Determinando a amostra por estrato
Estrato N Wi n'i
Rural 10000 0.1086957 27
Industrial 5000 0.0543478 13
Residencial 77000 0.8369565 205
Total 92000 1 245

12. Margem de erro pré-estabelecida
• Para determinar o tamanho da amostra a ser
sorteada utiliza-se para população infinita:
L
z / 2  Wi
2
i
2
n i 1
 2
• Em que W é o peso de cada estrato, i é o desvio
padrão do estrato i,  é o erro amostral e z/2 é o grau
de confiança.

13. Margem de erro pré-estabelecida
• Para determinar o tamanho da amostra a ser
sorteada utiliza-se para população finita:
L
z2 / 2  Wi i2
i 1
n 2
 2 L 2
 z / 2  Wi i 
1 N  i 1 
 2
• Em que W é o peso de cada estrato, i é o desvio
padrão do estrato i,  é o erro amostral e z/2 é o grau
de confiança.

14. Margem de erro pré-estabelecida
• Determina-se n’i fazendo:
n'i  Wi n
• Desta forma considera-se que todos os estratos tem
o mesmo desvio padrão.
• Se os desvios padrão forem diferentes para cada
estrato:
nWi i
n'i  L
W 
i 1
i i

15. Custo pré determinado
• Para determinar o tamanho da amostra a ser
sorteada utiliza-se:
Wi i
L
C 0 z / 2 
2
i 1 Ci
n
Wi i
L

i 1 Ci
• Em que Ci é o custo por unidade no estrato i, C0 é o
orçamento disponível, Wi é o peso do estrato i, i é o
desvio padrão do estrato i e z/2 é o grau de
confiança.

16. Custo pré determinado
• Determina-se n’i fazendo:
n'i  Wi n
• Desta forma considera-se que todos os estratos tem
o mesmo desvio padrão e mesmo custo de serem
amostrados.
• Se os desvios padrão forem diferentes para cada
estrato, mas tiverem o mesmo custo:
nWi i
n'i  L
W 
i 1
i i

17. Custo pré determinado
• Se os desvios padrão e os custos por unidade dos
estratos forem diferentes, tem-se :
Wi i
n
Ci
n'i  L
Wi i
 C
i 1 i
• Caso o desvio padrão não seja conhecido, é
necessário utilizar um dos procedimentos descritos
anteriormente.

18. Outros procedimentos amostrais
• Amostragem sistemática
• Amostragem por quotas
• Amostragem por conglomerados
• Amostragem em múltiplos estágios.

19. Inferência Estatística
Definição:
População é a função de probabilidade, no caso
discreto, ou função densidade de
probabilidade, no caso contínuo, de uma
variável aleatória X, que modela uma
característica de interesse.

20. Estatísticas e parâmetros
Depois de obtida uma amostra, desejamos
usá-la para produzir alguma característica de
interesse, por exemplo, calcular a média da
amostra (X1, X2,...,Xn).
1
X  ( X1  X 2    X n )
n
 A média é um exemplo de estatística.

21. Estatísticas e parâmetros
Uma estatística descreve uma característica
da AMOSTRA, ou seja, uma estatística T é uma
função de X1, X2,...,Xn
n n
 Xi  ( X i  X )2
X i 1
S2  i 1
n n 1
X (1)  min( X 1 , X 2 ,, X n )
X ( n)  max( X 1 , X 2 ,, X n )

22. Estatísticas e parâmetros
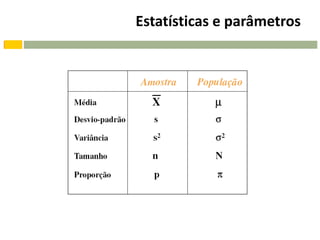
Um parâmetro é uma medida usada para
descrever um característica da POPULAÇÃO.
  E[X ]  2  Var[ X ]

23. Estatísticas e parâmetros

24. Distribuições amostrais
 Considere uma amostra aleatória de n
elementos sorteados da população.
 Nossa afirmação será baseada numa
estatística T, que será função da amostra (X1,
X2, ..., Xn ).
 Na amostra observamos um particular valor
de T, que chamaremos de t0, e com base
nesse valor, fazemos afirmações sobre um
parâmetro  (da população).

25. Distribuições amostrais
 A validade de nossas afirmações é melhor
compreendida quando sabemos o
comportamento (distribuição) de T.
 Isso acontece quando retiramos todas as
possíveis amostras de tamanho n da
população
Denominado de distribuição amostral da
estatística T.

26. Distribuições amostrais
Esquematicamente, temos:
– Uma população X, com determinado parâmetro de
interesse ;
– Todas as amostras retiradas da população, de acordo com
certo procedimento (AAS);
– Para cada amostra, calculamos o valor t0 da estatística T; e,
– Os valores t formam uma nova população, cuja
distribuição recebe o nome de distribuição amostral de T.

27. Distribuições amostrais
Exemplo: Considere a população {1,3,5,7}
Definimos a variável X: valor assumido pelo elemento da população.
A distribuição de X é dada por:
x 1 3 5 7
P(X = x) 1/4 1/4 1/4 1/4
Considere agora todas as amostras possíveis de tamanho 2
com reposição desta população. Indicamos por X1 o
número selecionado na primeira extração e por X2 na
segunda.

28. Distribuições amostrais
Qual a distribuição conjunta de (X1, X2)?
X2 1 3 5 7 Total
X1
1 1/4*1/4=1/16 1/16 1/16 1/16 4/16
3 1/16 1/16 1/16 1/16 4/16
5 1/16 1/16 1/16 1/16 4/16
7 1/16 1/16 1/16 1/16 4/16
Total 4/16 4/16 4/16 4/16 1

29. Distribuições amostrais
Qual a distribuição da estatística X  X 1  X 2 ?
2
Quando a amostra selecionada é o par (1,1) a média será
11
. , então a P( X =1)=1/16
1
2
Quando a média é igual a três temos os eventos
(5,1),(3,3),(1,5)
Logo P( X =3)=1/16+1/16+1/16 = 3/16

30. Distribuições amostrais
Distribuição amostral da estatística T
X 1 2 3 4 5 6 7 Total
P( X = x) 1/16 2/16 3/16 4/16 3/16 2/16 1/16 1
Gráfico da função de probabilidade e função de
distribuição:

31. Distribuições amostrais
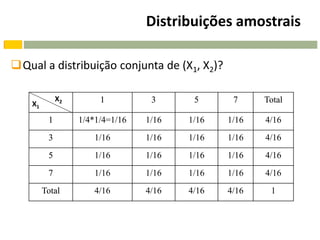
A população {1,3,5,7} tem média =4 e variância 2=5.
A média da distribuição amostral de T é:
n
1 2 3 1 64
E[ X ]   xi pi 1  2  3    7  4
i 1 16 16 16 16 16
2
Var[ X ]  E[ X ]  E 2 [ X ]  18,5  16  2,5

32. Distribuições amostrais
A média das médias amostrais coincide com a média da
população e a variância da média é igual a variância de X
dividida por n=2.
Exercício: Encontre a distribuição amostral de S2
n
 ( X i  X )2
S2  i 1
n 1

33. Distribuições amostrais
1o passo:
Calcular a estatística S2 para todas as amostras de dois
elementos (X1,X2).
S2 1 3 5 7
1 0 2 8 18
3 2 0 2 8
5 8 2 0 2
7 18 8 2 0

34. Distribuições amostrais
2o passo:
Calcular a distribuição de S2:
S2 0 2 8 18
P(S2 = x) 4/16 6/16 4/16 2/16
Quando trabalhamos com populações identificadas por
distribuição de probabilidades, não podemos gerar todas
as amostras possíveis. É necessário determinar
propriedades mais gerais

35. Distribuições amostral da média
Considere uma variável aleatória X cujos parâmetros são
 a média populacional e 2 a variância populacional.
Temos as propriedades:

36. Teorema do limite central

37. Teorema do limite central
• O teorema central do limite é muito importante, pois
permite utilizar a distribuição normal para realizar
inferências da média amostral, seja qual for a forma
da distribuição da população.

38. Teorema do limite central
 Quanto maior for o tamanho n da amostra, mais a média amostral
se aproximará da média da população.
 As propriedades da distribuição amostral asseguram que a média
de uma amostra é uma boa estatística para inferir sobre a média da
população  da qual foi extraída.
 Ao mesmo tempo, o teorema do limite central estabelece que se o
tamanho da amostra n for suficientemente grande a distribuição da
média amostral será normal, qualquer que seja a forma da
distribuição da população.
 Portanto, o teorema do limite central permite aplicar a distribuição
normal para obter respostas da média de uma amostra de tamanho
suficientemente grande retirada de uma população qualquer.

39. Desvio padrão amostral
O desvio padrão é conhecido como erro amostral.
 O desvio padrão da distribuição das médias amostrais diminui
quando aumenta o tamanho da amostra n.
 Isso significa que à medida que n aumenta e mais informações
são utilizadas, a média da amostra se aproxima da média da
população, como pode-se ver na expressão do desvio padrão.

X 
n

40. Distribuição amostral de uma proporção
 Considere uma população em que a proporção de indivíduos
portadores de uma característica é p. Então define-se a variável
aleatória X:
1 se o indivíduo for portador da característica
X 
0 se o indivíduo NÃO for portador da característica
 X tem distribuição de Bernoulli, com média =p e variância
2=p(1-p)

41. Distribuição amostral de uma proporção
Retirando uma AAS de tamanho n dessa população, e
indicando por Yn o total de indivíduos portadores da
característica na amostra:
Yn ~ Bin(n,p)
A proporção de indivíduos portadores da
característica na amostra é definida por:
Estatística T:
Yn
p
ˆ
n

42. Distribuição amostral de uma proporção
• De acordo com o teorema do limite central a
ˆ
distribuição amostral de p pode ser aproximada pela
distribuição normal
 2   p(1  p) 
p ~ N  , 
ˆ ˆ
p ~ N  p, 
 n   n 
 

43. Exercício 1

44. Exercício 2
• O número de divórcios, por indivíduo adulto casado, em certa
comunidade, foi modelado pela variável aleatória D, cuja função
de probabilidade é apresentada a seguir:
D 0 1 2 3
P(D=x) 0,5 0,4 0,05 0,05
• Uma amostra, representada por (D1,D2), foi sorteada com dois indivíduos e as
seguintes estatísticas para média de divórcios foram consideradas:
1  D1D2 2  max  min
• Para cada estatística obtenha sua distribuição de probabilidade.
• Construa o histograma e o gráfico da função de distribuição.

45. Exercício 3
• Uma variável aleatória assume quatro valores
(-2, -1, 1, 2) com igual probabilidade. Para
amostras de tamanho dois, obtenha a
distribuição de S2 e verifique se ele é não
viesado.

46. Exercício 4

47. Exercício 4
• Uma variável de Bernoulli com probabilidade
de sucesso p é amostrada, de forma
independente, duas vezes.
• Apresente a função de probabilidade da
média amostral.