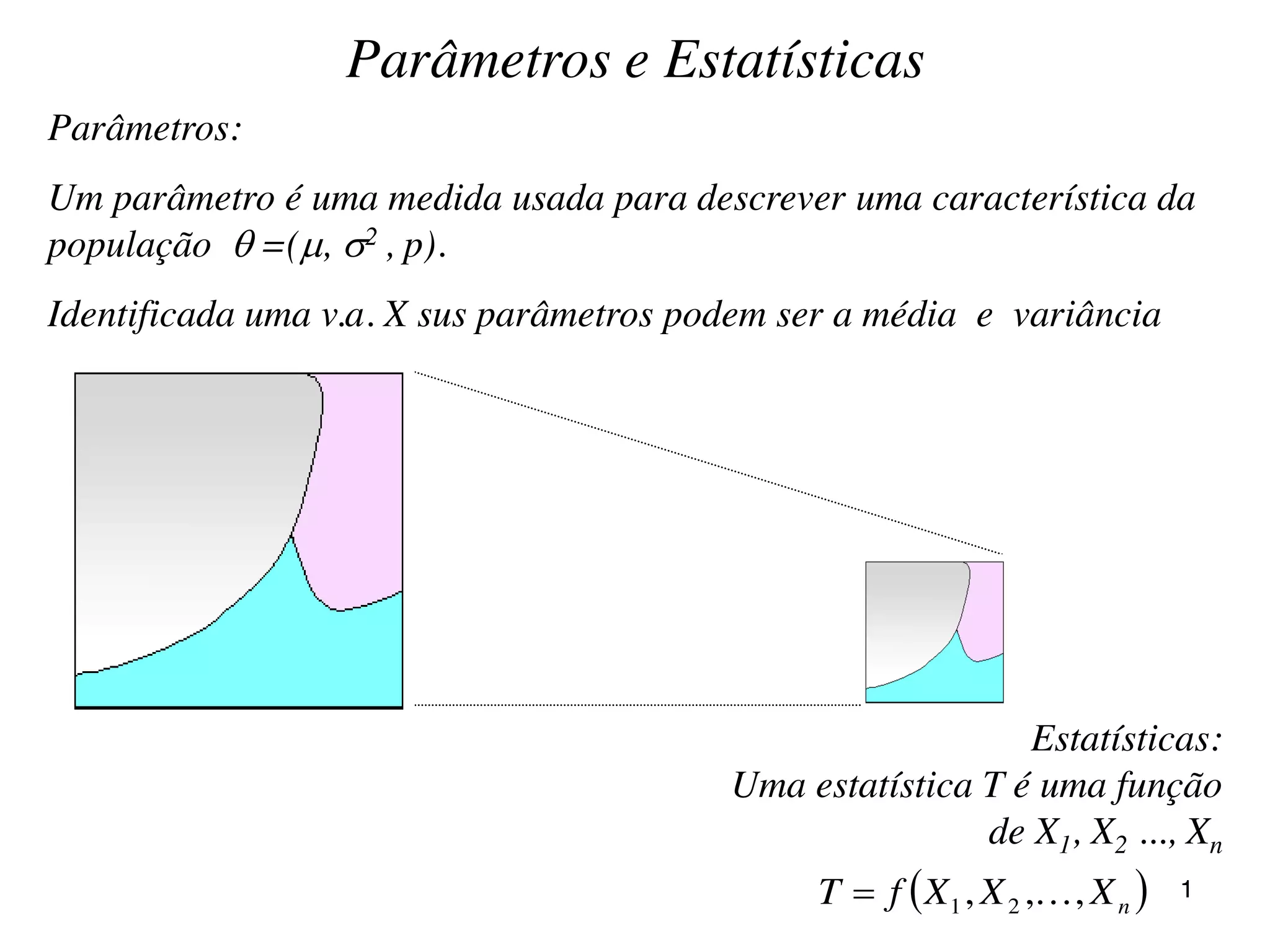
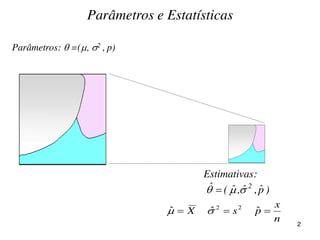
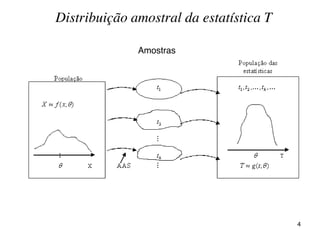
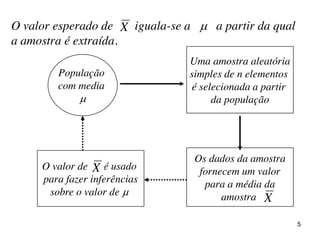
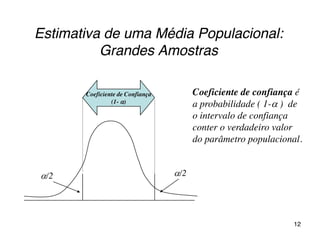
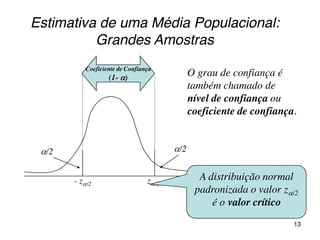
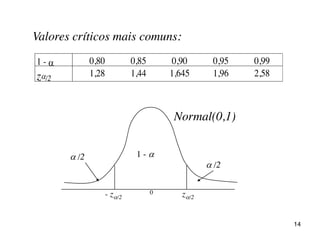
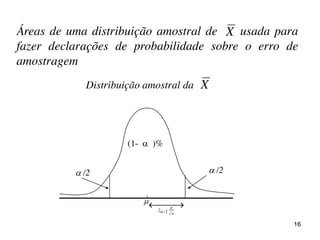
O documento discute parâmetros e estatísticas populacionais e amostrais. Define parâmetros como medidas que descrevem características da população e estatísticas como funções de variáveis aleatórias amostrais. Explica como estimativas amostrais como média e proporção são usadas para fazer inferências sobre parâmetros desconhecidos da população. Também cobre intervalos de confiança para média, variância e proporção populacionais.

1. Parâmetros:
Um parâmetro é uma medida usada para descrever uma característica da
população  =(, 2 , p).
Identificada uma v.a. X sus parâmetros podem ser a média e variância
Estatísticas:
Uma estatística T é uma função
de X1, X2 ..., Xn
Parâmetros e Estatísticas
 nXXXfT ,,, 21  1

2. Parâmetros e Estatísticas
)pˆ,ˆ,ˆ(ˆ 2
 
Parâmetros:  =(, 2 , p)
Estimativas:
n
x
psX  ˆˆˆ 22

2

3. )(X  n
Xi
X
)(2
XVar
  )1/()( 22
nXxS i
Denominação População Amostra
N de elementos N n
Média
Variância
Proporção p pˆ
Símbolos mais comuns a seguir
3

4. Amostras
Distribuição amostral da estatística T
4

5. População
com media

Uma amostra aleatória
simples de n elementos
é selecionada a partir
da população
Os dados da amostra
fornecem um valor
para a média da
amostra X
O valor de é usado
para fazer inferências
sobre o valor de 
X
O valor esperado de iguala-se a  a partir da qual
a amostra é extraída.
X
5
1
23
4

6. Teorema Central do Limite
Dado que :
• A variável aleatória X tem distribuição (que pode ser
normal, ou não), com média  e desvio padrão .
• Amostra de tamanho “n” são extraídas aleatoriamente
dessa população.
6

7. Teorema Central do Limite
Conclusões:
• Na medida que o tamanho da amostra aumenta, a distribuição
das médias amostrais tende para uma distribuição normal.
• A média das médias amostrais será a média populacional.
• O desvio padrão das médias amostrais será
 x
nx
 
7

8. Teorema Central do Limite
Regras Práticas de Uso Comum:
• Para amostras de tamanho n > 30, a distribuição das médias
amostrais pode ser aproximada satisfatoriamente por uma
distribuição normal.
• Se a própria distribuição original tem distribuição normal,
então as médias amostrais terão distribuição normal para
qualquer tamanho amostral n.
X
8

9. Intervalo de Confiança IC
Um intervalo de confiança (ou estimativa intervalar) é
uma amplitude (ou um intervalo) de valores que tem
probabilidade de conter o verdadeiro valor do
parâmetro populacional.
 =(,2 , p)
)()( xUxL 
9

10. Intervalo de Confiança IC
A partir de uma amostra de uma distribuição f(x,), que
depende de um parâmetro  desconhecido, desejamos
encontrar um intervalo aleatório que contenha  com alta
probabilidade
é chamado de intervalo de confiança (1-) se
)()( xUxL 
    1)()(Pr xUxL
10

11. Estimação:
Um estimador é uma estatística amostral utilizada para
obter uma aproximação de um parâmetro populacional.
)pˆ,ˆ,ˆ(ˆ 2
 
Uma estimativa pontual é um valor (ou ponto) único
usado para aproximar um parâmetro populacional.
n
x
psX  ˆ,ˆ,ˆ 22

11

12. Estimativa de uma Média Populacional:
Grandes Amostras
Coeficiente de confiança é
a probabilidade ( 1- ) de
o intervalo de confiança
conter o verdadeiro valor
do parâmetro populacional.
Coeficiente de Confiança
(1- )
/2/2
12

13. Coeficiente de Confiança
(1- )
/2/2
z/2- z/2
A distribuição normal
padronizada o valor z/2
é o valor crítico
O grau de confiança é
também chamado de
nível de confiança ou
coeficiente de confiança.
Estimativa de uma Média Populacional:
Grandes Amostras
13

14. Valores críticos mais comuns:
1 -  0,80 0,85 0,90 0,95 0,99
z/2
1,28 1,44 1,645 1,96 2,58
 /2
 /2 1 - 
0 z/2- z/2
Normal(0,1)
14

15. A margem de erro, denotado por E é a diferença máxima
provável (com probabilidade 1- ) entre a média amostral
observada e a verdadeira média populacional  .X
A margem de erro pode ser obtida multiplicando-se o valor
crítico pelo desvio padrão das médias amostrais,
n
.zE 2


Margem de Erro
15

16. Áreas de uma distribuição amostral de usada para
fazer declarações de probabilidade sobre o erro de
amostragem
 /2 /2
Distribuição amostral da X
(1-  )%

X
 
n
z 
 2/
16

17. Tamanho da Amostra para estimar 
Pode-se aplicar a fórmula E também para determinar o
tamanho da amostra que é necessário para atingir um grau de
precisão desejado .
Resolvendo a equação do erro em n obtemos,
2
2







E
z
n

n
.zE 2


17

18. Intervalo de Confiança para a média populacional  (com
base a grandes amostras: n > 30)
EXEX   Onde n
.zE 2









n
zX;
n
zX
22


Outras formas equivalentes de escrever:
• com variância conhecida o intervalo de confiança 100(1-)%
para 
Intervalo de Confiança (IC) para 
• com variância desconhecida, usa-se a distribuição
normal com o estimador s2 de 2 .
18

19. Intervalo de Confiança (IC) para 
Exemplo 1: Sejam X1, X2, ... X40 uma amostra aleatória de uma
variável aleatória que tem distribuição Normal com média
desconhecida e variância  = 410. Se encontre um
intervalo de confiança 95% para ..
1428X
Olhando a tabela da Distribuição Normal, temos que o ponto crítico,
tal que
Se  = 0,05, temos que z0,025 = 1,96.
  2/2/   zZP
19

20. Intervalo de Confiança (IC) para 
Pr[Z > 1,96 ] = 0,025Pr[Z < - 1,96]= 0,025
- 1,96
Pr[-1,96 < Z < 1,96] = 0,95
1,96
O IC de 95% de confiança para a  é [1300,85 ; 1555,15]
20
X - z(∝/2)*σ/√n =
= 1428 - 1,96*410/√40 =
= 1.300,94
X + z(∝/2)*σ/√n =
= 1428 + 1,96*410/√40 =
= 1.555,06

21. Intervalo de Confiança para a média populacional 
(com base a pequenas amostras: n < 30)
Variáveis aleatórias independentes, então:
• com variância desconhecida
Intervalo de Confiança (IC) para 
Pode-se mostrar que:
e2
1n
2
~
S)1n(




  )1,0(Normal~
X
n


 
1nt~
S
Xn

 
21

22. Intervalo de Confiança para a média populacional  (com
base a pequenas amostras: n < 30)






 
n
s
tX
n
s
tX nn 11 ;
• com variância desconhecida
Intervalo de Confiança (IC) para 
O intervalo de confiança 100(1-)% para 
Onde t é o percentil (1 - /2) da distribuição de Student
com n -1 graus de liberdade.
22

23. Intervalo de Confiança (IC) para 






 
n
s
tX
n
s
tX nn 11 ;
 /2 /2
tn-1- tn-1
Pr[ t > tn-1] = /2
Ex. Se n = 10 e  = 0,05, temos Pr[ t < 2,262] = 0,975
23

24. Intervalo de Confiança (IC) para 
Exemplo 2: Sejam X1, X2, ... X40 uma amostra aleatória
de uma variável aleatória que tem distribuição Normal
com média e variância desconhecidas. Dado que
e s= 496, encontre um intervalo de confiança 95% para
.
1428X
Se n > 30, então usa-se a distribuição normal com
estimador s2 de 2.
24

25. Intervalo de Confiança (IC) para 
Pr[Z > 1,96 ] = 0,025Pr[Z < - 1,96]= 0,025
- 1,96
Pr[-1,96 < Z < 1,96] = 0,95
1,96
O IC de 95% de confiança para a  é [1274,18 ; 1581,82]
25
X - t(n-1)*s/√n =
= 1428 - 1,96*496/√40 =
= 1.274,29
X - t(n-1)*s/√n =
= 1428 + 1,96*496/√40 =
= 1.581,71

26. Intervalo de Confiança (IC) para 
Exemplo 3: Sejam X1, X2, ... X25 uma amostra aleatória de uma
variável aleatória que tem distribuição Normal com média e
variância desconhecidas. Dado que e s2 = 36, encontre um
intervalo de confiança 95% para .
15X
Olhando a tabela da Distribuição t de Student, temos que o ponto
crítico t24,0,025=2,064 então
Pr[t24 > 2,064] = 0,025.
26

27. Intervalo de Confiança (IC) para 
Pr[t > 2,064 ] = 0,025Pr[t < - 2,064]= 0,025
- 2,064
Pr[-2,064 < t < 2,064] = 0,95
2,064
O IC de 95% de confiança para a  é [ 12,523 ; 17,477]
27
X + t(n-1)*√s²/√n =
= 15 + 2,064*√36/√25 =
= 17,477
X - t(n-1)*√s²/√n =
= 15 - 2,064*√36/√25 =
= 12,523

28. Lembrando que quando p populacional é conhecida, tem
distribuição assintotica
.
 pp zpzp ˆ0ˆ0 22
ˆ;ˆ   
Logo, temos que o IC para a proporção populacional ao nível de
significância (1-) :
Intervalo de Confiança (IC) para proporções
n
x
p ˆ







n
pq
pNp ,ˆ
Para construir o IC para p desconhecida, determinarmos na
amostra e consideremos
0
ˆp
n
qp
p
00
ˆ
ˆˆ

28

29. Exemplo: Retiramos de uma população uma amostra de 100
elementos e encontramos 20 sucessos. Ao nível de 1%, construir um
IC para a proporção real de sucessos na população.
Intervalo de Confiança (IC) para proporções
29
O IC de 99% de confiança para p é [ 0,0972; 0,3028]
p(o) - z(∝/2)*σ(p) =
= 0,01 - 2,58*?? =
=
p(o) + z(∝/2)*σ(p) =
= 0,01 + 2,58*?? =
=

30. Aumentando o tamanho da amostra para melhorar a precisão.
•Uma maneira de melhorar a precisão do intervalo de confiança sem
diminuir o nível de confiança é aumentar o tamanho da amostra.
Obtendo o tamanho mínimo da amostra para estimar p
Dado um nível de confiança (1-) e um erro máximo de estimativa E, o
mínimo tamanho necessário da amostra para estimar p é
Essa formula supõe que haja uma estimativa preliminar para e .
Caso não seja assim, use e
30
2
2/
ˆˆ 






E
z
qpn 
pˆ qˆ
5,0ˆ p 5,0ˆ q

31. Determinando um tamanho mínimo para a amostra.
•Você é auxiliar em uma campanha política e deseja estimar, com 95%
de confiança, a proporção de eleitores registrados que votarão em seu
candidato.
•Qual é o mínimo tamanho necessário da amostra para estimar a
proporção populacional com precisão dentro de 3%?
Solução: Uma vez que não temos estimativas preliminares usaremos
e . Usando e E=0,03 temos que
Pelo menos 1.068 eleitores registrados devem ser incluídos na amostra.
Exemplo
5,0ˆ p
31
5,0ˆ q 96,12/ z
11,1067
03,0
96,1
)5,0)(5,0(ˆˆ
22
2/













E
z
qpn 

32. População Normal com média  desconhecida.
    









 


1
11
2
1
2
2
2
2
2
snsn
P
Logo, o IC para a proporção populacional ao nível de significância
(1-) :
Intervalo de Confiança (IC) para a variância
  2
1
2
1
2


 n
n
i
i xx 
Demostra-se que tem distribuição relacionada com
com (n-1) graus de liberdade, isto é,
 

n
i
i xx
1
2 2

Como temos  

 22
1
1
xx
n
s i
    2
1
2
1 snxx
n
i
i 
  22
1
2
1 snn  
32

33.     









 


1
11
2
1
2
2
2
2
2
snsn
P
O IC para a variância populacional ao nível de significância (1-) :
Intervalo de Confiança (IC) para a variância
Onde: e
2
)%2/(,1
2
1   n
2
)%2/1(,1
2
2   n
33

34. Exemplo: Sabe-se que o tempo de vida de certo tipo de válvula tem
distribuição aproximadamente normal. Uma amostra de 25 válvulas
forneceu média amostral de 500 h e s=50 h. Construir um IC para
2, ao nível de 2%.
Intervalo de Confiança (IC) para a variância
Se n = 25, s2=2500 856,102
%1,24
2
1   980,422
%99,24
2
2  
    









 


1
11
2
1
2
2
2
2
2
snsn
P
34
O IC de 98% de confiança para 2 é [ 1395,9; 5526,9]
(n-1)*s²/x2² =
= (25-1)*2500/42,980 =
= 1.396
(n-1)*s²/x1² =
= (25-1)*2500/10,856 =
= 5.526,90