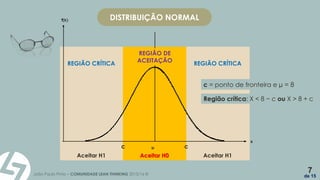
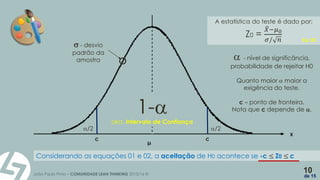
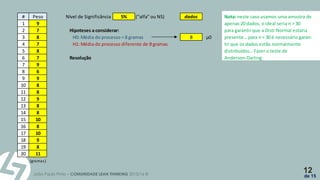
O documento apresenta os conceitos básicos de testes de hipóteses estatísticas, incluindo a definição de hipótese nula (h0) e hipótese alternativa (h1), bem como os procedimentos para conduzir esses testes. Exemplos práticos ilustram como avaliar se uma máquina de encher pacotes de açúcar está a funcionar corretamente com base em amostras coletadas. O texto enfatiza a importância da escolha do nível de significância e a interpretação dos resultados obtidos nos testes.

1. TESTES DE HIPÓTESES
MATERIAL DE SUPORTE AO 6 - XVI EDIÇÃO DA PG LEAN MANAGEMENT
JOÃO PAULO PINTO – 2015 JUNHO 13

2. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
2
de 15
APRESENTAÇÃO DO CONCEITO
 Considere-se uma máquina de encher pacotes de açúcar…
 O peso de cada pacote deve ser ≈ 8g (isto é, µ = 8);
 Será que a máquina está a funcionar correctamente?
D E F I N I Ç Ã O
Uma hipótese estatística é uma afirmação acerca dos parâmetros de
uma ou mais populações (testes paramétricos) ou acerca da
distribuição da população (testes de ajustamento).
Vamos abordar os testes paramétricos…

3. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
3
de 15
 De volta aos pacotes de açúcar…
 Temos duas hipóteses:
 A máquina funciona correctamente (µ = 8)  H0 :µ = 8
Esta é chamada de hipótese nula (H0)
 A máquina não funciona correctamente (µ ≠ 8)  H1 :µ ≠ 8
Esta é chamada de hipótese alternativa (H0)
Para H0 temos ainda a considerar:
 Hipótese simples: é especificado apenas um valor para o parâmetro;
 Hipótese composta: é especificado mais de um valor para o parâmetro.
 Por agora vamos considerar sempre H0 como hipótese simples…

4. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
4
de 15
Para a hipótese alternativa H1 temos a considerar:
 H1 :µ ≠ 8 hipótese alternativa bilateral
 H1 :µ > 8 hipótese alternativa unilateral (superior)
 H1 :µ < 8 hipótese alternativa unilateral (inferior)
D E F I N I Ç Ã O
Teste de hipóteses é um procedimento que conduz a uma decisão
acerca das hipóteses (com base numa amostra aleatória).

5. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
5
de 15
ALGUNS COMENTÁRIOS SOBRE AS HIPÓTESES
1. A hipótese nula (H0) representa o status quo ou crença atual em uma situação;
2. A hipótese alternativa (H1) é o oposto da hipótese nula e representa uma questão
de investigação que se pretende estudar;
3. Se rejeitarmos H0, então temos a prova estatística de que H1 é verdadeira;
4. Se não rejeitarmos H0, então não foi possível provar a hipótese alternativa, H1.
Falhar a demonstração de H1 não quer dizer que H0 esteja demonstrada;
5. A hipótese nula (H0) refere-se sempre a um valor especifico da população (ex. μ)
e não uma estatística da amostra (como media da amostra, |X);
6. A declaração de H0 tem sempre um sinal de igual em relação ao valor
especificado do parâmetro (por exemplo, H0: μ1 = μ2);
7. A declaração da hipótese alternativa nem sempre contém um sinal de igual em
relação ao valor do parâmetro especificado (por exemplo, H1: μ1 ≠ μ2).

6. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
6
de 15
 Voltando aos pacotes de açúcar…
 Considere X uma variável aleatória que representa o peso de um pacote de
açúcar, então temos:
 E(X) = µ e V(X) = σ2 (variância).
 Logo, H0 :µ = 8 vs H1 :µ ≠ 8
 Agora dispomos de uma amostra de 10 observações: X1 a X10;
 Então faz sentido decidir com base em X , aceitando H0 se X estiver
próxima de 8 e rejeitando H0 se X estiver longe de 8…
 Observemos a figura que se segue…

7. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
7
de 15
Aceitar H1Aceitar H1 Aceitar H0
DISTRIBUIÇÃO NORMAL
REGIÃO CRÍTICAREGIÃO CRÍTICA
REGIÃO DE
ACEITAÇÃO
c = ponto de fronteira e µ = 8
cc
Região crítica: X < 8 − c ou X > 8 + c

8. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
8
de 15
PROCEDIMENTO GERAL
DO TESTE DE HIPÓTESES
1. Pelo contexto do problema identificar o parâmetro de interesse;
2. Especificar a hipótese nula, H0;
3. Especificar uma hipótese alternativa apropriada, H1;
4. Escolher o nível de significância α (é a probabilidade de
rejeitar H0 sendo ela verdadeira);
5. Escolher uma estatística de teste adequada, ie Z0;
6. Fixar a região crítica do teste (µ +/- c);
7. Recolher uma amostra (de tamanho n) e calcular o valor
observado da estatística de teste;
8. Decidir sobre a rejeição, ou não, de H0.

9. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
9
de 15
TESTE DE HIPÓTESES PARA MÉDIA
E VARIÂNCIA CONHECIDAS
 Considere a população de X tal que:
E(X) = µ (desconhecido) V(X) = σ 2 (conhecido)
Para valores de X1 a Xn e amostra de dimensão n
 Teste de hipóteses: H0: µ = µ0 vs H1: µ ≠ µ0
Assim:
 Rejeita-se H0 se 𝑋 < 𝜇0 − 𝑐 ∗
𝜎
𝑛
ou 𝑋 > 𝜇0 + 𝑐 ∗
𝜎
𝑛
 E não se rejeita H0 se 𝜇0 − 𝑐 ∗
𝜎
𝑛
≤ 𝑋 ≤ 𝜇0 + 𝑐 ∗
𝜎
𝑛
Considere de novo a Dist Normal para perceber melhor…
Eq. 01

10. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
10
de 15
1-
aka, Intervalo de Confiança
 - nível de significância,
probabilidade de rejeitar H0
Quanto maior  maior a
exigência do teste.
c – ponto de fronteira.
Nota que c depende de .
/2 /2
c c
 - desvio
padrão da
amostra
A estatística do teste é dado por:
Z0 =
𝑋−𝜇0
𝜎/ 𝑛 Eq. 02
Considerando as equações 01 e 02, a aceitação de H0 acontece se -c ≤ Z0 ≤ c

11. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
11
de 15
EXERCÍCIO 1.
 Voltando ao pacote de açúcar…
 Recolhemos uma amostra de 20 pacotes, ver ao lado 
 Assuma um nível de significância de 5% (ie, o risco de rejeitar
H0 sendo ela verdadeira);
 Pretende-se saber se a máquina está afinada tendo como base
esta amostra (n = 20) para H0: µ = 8 gramas
A resposta é: Aceitar H0, ou seja para este nível de significância
() podemos considerar que a máquina está afinada.
E se aumentarmos o valor de  o que se pode esperar?
O que significa um aumento desse parâmetro?
# Peso
1 9
2 7
3 8
4 7
5 8
6 7
7 9
8 6
9 9
10 8
11 8
12 9
13 8
14 8
15 10
16 8
17 10
18 9
19 8
20 11
(gramas)Ver file xlsx

12. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
12
de 15
# Peso Nível de Significância 5% ("alfa" ou NS) dados Nota: neste caso usamos uma amostra de
1 9 apenas 20 dados, o ideal seria n > 30
2 7 Hipoteses a considerar: para garantir que a Distr Normal estaria
3 8 H0: Média do processo = 8 gramas 8 µ0 presente… para n < 30 é necessário garan-
4 7 H1: Média do processo diferente de 8 gramas tir que os dados estão normalmente
5 8 distribuídos… Fazer o teste de
6 7 Resolução Anderson-Darling
7 9 Média da amostra 8,35 gramas (X barra)
8 6 Desvio da Amostra 1,18 gramas
9 9
10 8 Estatística do Teste, Z0 1,3241207
11 8
12 9 Com o valor de "alfa" (NS) obtém-se "c" (necessário obter a área da Distrib Normal):
13 8 área da Distr Normal =1-1/2*NS
14 8 área = 0,975 ou 97,50% Consultar agora a Distr Normal para obter "c"
15 10 Ponto de Fronteira "c" = 1,96
16 8
17 10 Aceitação ou rejeição da Hipotese Nula (H0) - decisão tomada com base em "c" e "Zo":
18 9
19 8 -1,96 < 1,3241207 < 1,96
20 11
(gramas)
Aceita Ho
Aceita Ho

13. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
13
de 15
EXERCÍCIO 2.
 Suponha que a média de todas as notas do M1 da PG-LM (das 17 edições,
mais de 500 formandos) é 12 valores com desvio padrão 6;
 Na actual turma (30 formandos), a média deste módulo é 16;
 Research question: Posso afirmar que a actual turma é significativamente
diferente de todos os formandos da PG LM (a população)?
Resolução
 H0: µ = 12 H1:  ≠ 12
 Z0 = 3.65 Para  = 5% temos c = 1.96
 Rejeitamos Ho ou seja esta turma é significativamente diferente…

14. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
14
de 15
EXERCÍCIO 3.
 Suponha que queremos saber se há diferença nos salários para os
professores masculinos e femininos;
 Poderíamos obter duas amostras (homens e outra de mulheres), para
determinar os respectivos níveis salariais médios (M1 e M2);
 M1 e M2 são estimativas das medias da população, 1 e 2.
 Formule as hipóteses nula e alternativa.
Resposta:
 Ho: 1 = 2
 H1: 1  2
 Suponha que a crença é que eles ganham mais que elas…
Formule de novo as hipóteses…
H1: 1 - 2 > 0

15. João Paulo Pinto – COMUNIDADE LEAN THINKING 2015/16 ©
15
de 15
EXERCÍCIO 4.
 Um fabricante de lâminas de barbear afirma que suas lâminas
dão em média 15 boas intervenções;
 Foi feito um teste, pedindo a 10 homens escolhidos aleatoriamente para testar
as lâminas de. O número médio de boas intervenções relatados é de 13 e o
desvio padrão é 3.62;
 O fabricante insiste que o verdadeiro número de acções (ou valor da
população) é 15… (não seria de esperar outra coisa).
 Formule as hipóteses nula e alternativa…
Resposta:
 Ho:  = 15
 Se quisermos desafiar o fabricante: H1:  < 15
 Então se formos totalmente agnósticos: H1:   15

16. MUITO OBRIGADO
PELA ATENÇÃO
CLT VALUEBASED SERVICES
Av da República, 2491 – Sala 41, 4º Piso
4430 208 VN de Gaia
Telf. 93.600.00.79/88
Fax. 220.162.407
mgt@cltservices.net
www.cltservices.net