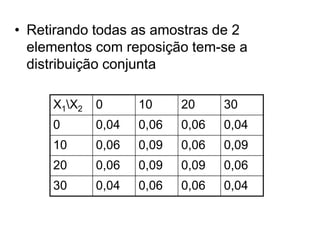
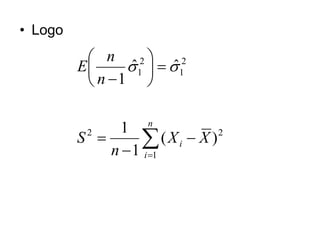Este documento discute estimação estatística. Ele define estimador como qualquer função da amostra que estima um parâmetro populacional e destaca a importância de um estimador ser não viciado, consistente e eficiente. Exemplos ilustram como calcular a esperança e variância de estimadores para estimar a média e variância populacional.

1. Aula 11
Estimação
Profa. Dra. Juliana Garcia Cespedes
Universidade Federal de Itajubá

2. Resumo
 A principal preocupação numa inferência estatística é obter
conclusões sobre a população.
 Com a média de uma amostra extraída de uma população será
estimada a média dessa população.
 Entretanto, de uma mesma população pode-se tomar muitas
amostras diferentes do mesmo tamanho.
O parâmetro média da população é um valor único e
desconhecido.
A estatística média da amostra é um valor
conhecido, porém pode variar de amostra para
amostra.

3. Resumo
 Com as médias das amostras, é possível construir a
distribuição de freqüências das médias das amostras,
denominada distribuição amostral da média, cuja média
denomina-se média amostral e seu desvio padrão, erro
padrão ou erro amostral.

4. Estimação
• Devido a natureza aleatória envolvida num
procedimento amostral (AAS), não podemos
garantir que repetições de amostras produzam
sempre resultados idênticos.
• Então, ao coletarmos uma amostra, não
podemos prever antecipadamente seu
resultado, ou seja, todas as quantidades
associadas à amostra terão caráter aleatório e
portanto, devem receber tratamento
probabilístico.

5. Estimação
• À combinação dos elementos da amostra,
construída com a finalidade de representar, ou
estimar, um parâmetro de interesse na
população denominamos estimador. Em geral,
denotamos os estimadores por símbolos com o
acento circunflexo: ^ ^ , etc.
, , ^
• Aos valores numéricos assumidos pelos
estimadores denominamos estimativas
pontuais ou estimativas

6. Estimação
• Def. Um estimador T do parâmetro  é
qualquer função da amostra, ou seja,
T=g(X1,...,Xn).
Um estimador é uma estatística associada a um parâmetro
populacional.
• Estimativa é o valor assumido pelo
estimador em uma amostra.

7. Estimação
• Mas qualquer função representa bem o parâmetro
em estudo?
• O estimador precisa ter algumas propriedades:
Vício: Um estimador é não viciado ou não viesado
para um parâmetro  se:
ˆ
E ( )  
Em outras palavras, um estimador é não viciado
se o seu valor esperado coincide com o
parâmetro de interesse.

8. Estimação
Consistência: Um estimador é consistente se, à
medida que o tamanho da amostra aumenta,
seu valor esperado converge para o parâmetro
de interesse e sua variância converge para
zero:
ˆ
i ) lim E ( )   ;
n  O estimador
depende de n !!
ˆ
ii ) lim Var ( )  0;
n 

9. Estimação
Eficiência: Dados dois estimadores ^ 1 e 2, não
 ^
viciados para um parâmetro . Dizemos que ^ 1 é

mais eficiente do que ^ 2 se:

ˆ ˆ
Var (1 )  Var ( 2 )

10. Parâmetro Estimador Propriedades
 X
n
i
Não viciado e
X i 1
consistente
n
p % com caracterís tica
Não viciado e
p
ˆ
n consistente
2 n
(X i  X )2 Não viciado e
S2  i 1
consistente
n 1
2 
n
( X i  X )2 Viciado e
2 
ˆ i 1 consistente
n

11. Exemplo
• Considere que, numa certa população,
uma variável aleatória X assuma os
valores 0, 10, 20 e 30 com porcentagens
20%, 30%, 30% e 20%, respectivamente.
Logo  = 15 e 2 = 105.
X 0 10 20 30
P(X=x) 0,2 0,3 0,3 0,2

12. • Retirando todas as amostras de 2
elementos com reposição tem-se a
distribuição conjunta
X1X2 0 10 20 30
0 0,04 0,06 0,06 0,04
10 0,06 0,09 0,06 0,09
20 0,06 0,09 0,09 0,06
30 0,04 0,06 0,06 0,04

13. • Para estimar  na população, considere
os estimadores:
1  X 1
ˆ
n
X i
2 
ˆ i 1
n
1
^ 0 10 20 30
P(1=x) 0,2 0,3 0,3 0,2
2
^ 0 5 10 15 20 25 30
P(2=x) 0,04 0,12 0,21 0,26 0,21 0,12 0,04

14. • Obtendo o valor esperado de 1 ,2:
^ ^
E ( 1 )  0 * 0,2  10 * 0,3  20 * 0,3  30 * 0,3  15
ˆ
E ( 2 )  0 * 0,04  5 * 0,12  10 * 0,21  ...  30 * 0,04  15
ˆ
• Portanto, os estimadores são não
viciados:
E ( 1 )  
ˆ
E (2 )  
ˆ

15. • Esses estimadores são consistentes?
Propriedade da Variância:
Var (aX )  a 2Var ( X )
i ) lim E (  1)  lim E ( X 1 )  lim 15  
ˆ
n  n  n 
ii ) lim Var (  1)  lim Var ( X 1 )  lim 105   2
ˆ
n  n  n 
n
 X 1  X 2  ...  X n   E( X i ) n
i ) lim E (  2)  lim E 
ˆ   lim i 1  lim 
n  n 
 n  n  n n  n
n
 X  X 2  ...  X n 
Var ( X ) i
n 2 2
ii ) lim Var (  2)  lim Var  1
ˆ   lim i 1
 lim 2  lim 0
n  n 
 n  n  n2 n  n n  n
Portanto,o estimador 1 não é consistente e o estimador 2 é consistente!!!

16. • Qual é o estimador mais eficiente?
Var (  1)   2  105
ˆ
2 105
Var (  2) 
ˆ   52,5
n 2
Portanto o estimador 2 é mais eficiente que o estimador 1.
Var (2 )  Var (1 )
ˆ ˆ

17. Trabalho em grupo para casa
• Mostre que o estimador da variância dividido por
n-1 é não viciado?
• Supondo uma amostra (X1,...,Xn) obtida de uma
população com média  e variância 2. Um
estimador natural da variância é:
n
(X i  X) 2
1 
ˆ 2 i 1
n

18. Estimação
• Esse estimador é viciado?
n n
 ( X i  X ) 2  ( X i      X ) 2
i 1 i 1
n n n
  ( X i   )  2 ( X i   )( X   )   ( X   ) 2
2
i 1 i 1 i 1
X  é uma constante e  ( X i   )  n( X   ) 2
n
• Como i 1
n n
 ( X i  X )   ( X i   ) 2  n( X   ) 2 .
i 1
2
i 1

19. • Segue que
 n 2
E  ( X i  X ) 
E ( 12 )   i 1
ˆ 
n
1 n 2
  E ( X i   )  nE ( X   ) 
2
n  i 1 
1 1 2
 n  
2
n n
 n 1  2
 
 n 

20. • Logo
 n 2
E ˆ1    12
ˆ
 n 1 
1 n
S 
2
(Xi  X )
n  1 i 1
2

21. Exercício 1
• Foi analisado uma população de 15 famílias
com filhos num certo bairro e observado o
número de crianças de cada família,
matriculadas na escola. Os dados foram:
1,1,2,0,2,0,2,3,4,1,1,2,0,0, e 2.
• Qual dos estimadores abaixo é o “melhor”
estimador da média e por quê?
(max  min) ( X1  X 2 )
 1
ˆ ; 2 
ˆ ;  3 X
ˆ
2 2

22. Exercício 2
• Suponha um experimento consistindo de n
provas de Bernoulli, com probabilidade de
sucesso p. Seja X o número de sucessos, e
considere os estimadores
X 1, se a primeira prova resultar sucesso,
p1  ;
ˆ p2  
ˆ
n  0, caso contrário.
• Determine a esperança e a variância de cada
^
estimador. Por que p2 não é um bom estimador?
• Verifique se ^ 1 e p2 são consistentes.
p ^